fntlr

テイラー係数

構文

taylor = fntlr(f,dorder,x)


説明

taylor = fntlr(f,dorder,x) は、f で記述された関数について、与えられた次数 dorder まで、与えられた x における非正規化テイラー係数を返します。

一変量関数とスカラー x の場合、これは次のベクトルになります。

$$T(f,\text{dorder},x):=[f(x);Df(x);\mathrm{...};D^{\text{dorder}-1}f(x)]$$

より一般的には、f の関数が d>1 (または、場合によっては prod(d)>1) の d 値であるか、m>1 などの場合の m 変量である場合、またはその両方の場合、dorder は正の整数の m ベクトルであると想定され、x は m 行の行列であると想定されます。その場合、出力のサイズは [prod(d)*prod(dorder),size(x,2)] で j 番目の列には次が含まれます。

$$T(f,\text{dorder},x(:,j))(i1,\mathrm{...},im)=D_1{}^{i1-1}\mathrm{...}{D}_m{}^{im-1}f(x(:,j))$$

これは、i1=1:dorder(1), ..., im=1:dorder(m) の場合です。ここで、D_if は、i 番目の引数に関する f の偏導関数です。

例

f に一変量関数が含まれ、x がスカラーまたは 1 行の行列の場合、fntlr(f,3,x) は次のステートメントと同じ出力を生成します。

df = fnder(f); [fnval(f,x); fnval(df,x); fnval(fnder(df),x)];

より複雑な例として、グラフが単位円である有理スプラインの場合の、21 の等間隔の点で次数が 3 のテイラー ベクトルを取り上げます。

ci = rsmak('circle'); in = fnbrk(ci,'interv');
t = linspace(in(1),in(2),21); t(end)=[];
v = fntlr(ci,3,t);

ci を点 v(1:2,:) と共にプロットして、これらが本当に単位円上にあることを検証します。

fnplt(ci), hold on, plot(v(1,:),v(2,:),'o')

次に、v(3:4,j) が点 v(1:2,j) で円に正接するベクトルであることを検証するために、MATLAB^® quiver コマンドを使用して、対応する矢印をプロットに追加します。

quiver(v(1,:),v(2,:),v(3,:),v(4,:))

最後に、v(5:6,:) についてはどうでしょうか。これらは 2 次導関数です。以下の quiver コマンドを使用して対応する矢印を追加すると、最終的に円を与える有理スプラインの 1 次および 2 次導関数になります。

quiver(v(1,:),v(2,:),v(5,:),v(6,:)), axis equal, hold off

円を与える有理スプラインの 1 次および 2 次導関数

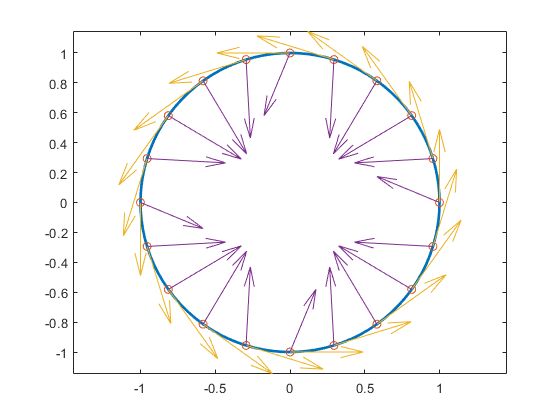
これで、曲線は円になりました。2 次導関数の矢印がまっすぐに円の中心を向くと予測したかもしれませんが、それはまさしく、ci の関数が弧の長さを独立変数として使用していた場合の結果です。使用されたパラメーターは弧の長さではないため、例: 円の B 型スプライン近似で示された式を使用して、選択した点で ci によって与えられた曲線の曲率を計算します。容易に比較できるように、そこで使用される変数に切り替え、単にそこからのコマンドを使用します。

dspt = v(3:4,:); ddspt = v(5:6,:);
kappa = abs(dspt(1,:).*ddspt(2,:)-dspt(2,:).*ddspt(1,:))./...
   (sum(dspt.^2)).^(3/2);
max(abs(kappa-1))
ans = 2.2204e-016

数値の解から、テストしたすべての点で、曲率が丸めの範囲内で 1 であることがわかります。

参考

fnder | fndir