有理スプラインの作成と操作
有理スプラインの例: 円
以下に例を示します。
circle = rsmak('circle');
は、その基本区間の値が単位円 (原点を中心とする半径 1 の円) を描く有理スプラインを提供します。これは、コマンド
fnplt(circle), axis square
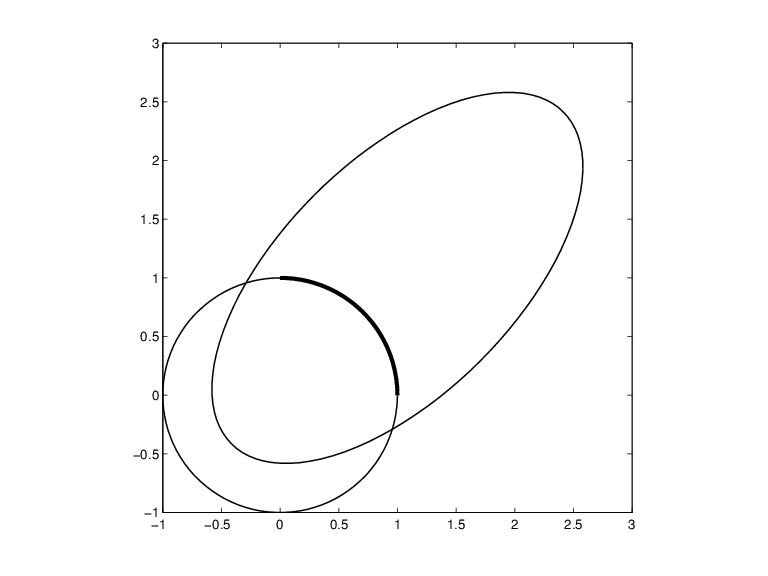
で容易にわかります。結果の出力は、Figure どちらも有理スプラインによって与えられた円と楕円の円となります。
この円を操作して、関連する形状を簡単に取得できます。たとえば、次のコマンドは円を楕円に引き延ばし、45 度回転させて、(1,1) で変換した後、円の上にプロットします。
ellipse = fncmb(circle,[2 0;0 1]); s45 = 1/sqrt(2); rtellipse = fncmb(fncmb(ellipse, [s45 -s45;s45 s45]), [1;1] ); hold on, fnplt(rtellipse), hold off
別の例として、作成された "円" は 4 つの区分から組み立てられています。1 番目の区分を強調表示するには、次のコマンドを使用します。
quarter = fnbrk(fn2fm(circle,'rp'),1); hold on, fnplt(quarter,3), hold off
1 番目のコマンドでは、fn2fm を使用して、B 型に基づく型から pp 型に基づく型へと型を変更し、その後、fnbrk を使用して 1 番目の区分を抽出しています。この区分が、それを目立たせるための線幅 3 でどちらも有理スプラインによって与えられた円と楕円内の円の上にプロットされます。
どちらも有理スプラインによって与えられた円と楕円
有理スプラインの例: 球体
面の例として、コマンド rsmak('southcap') は 3 ベクトル値の有理双三次多項式を提供します。この式が単位正方形 [-1 .. 1]^2 上にもつ値で単位球体の 1 区分が埋められます。それを 5 つの適切な回転に隣り合わせると、単位球体が正しく取得されます。説明のため、以下のコマンドは、4 次有理式の 4 つの回転により形成された球体の一部に示されるように、球体の 2/3 を生成します。
southcap = rsmak('southcap'); fnplt(southcap)
xpcap = fncmb(southcap,[0 0 -1;0 1 0;1 0 0]);
ypcap = fncmb(xpcap,[0 -1 0; 1 0 0; 0 0 1]);
northcap = fncmb(southcap,-1);
hold on, fnplt(xpcap), fnplt(ypcap), fnplt(northcap)
axis equal, shading interp, view(-115,10), axis off, hold off
4 次有理式の 4 つの回転により形成された球体の一部

有理スプラインを操作するための関数
この方法で通常のスプライン R=[s;w] によって有理スプライン r = s/w を表す方が、以下の例外を除き、すべての fn... コマンドを Curve Fitting Toolbox™ のスプライン関数で有理スプラインに簡単に適用できます。有理スプラインの積分が有理スプラインである必要はないため、fnint を有理スプラインに拡張する方法はありません。有理スプラインの微分 "は" 有理スプラインとなりますが、約 2 倍の次数となります。そのため、fnder と fndir が有理スプラインに接することはありません。代わりに、特定の関数の特定の次数までのすべての微分の特定の x における値を計算するためのコマンド fntlr があります。その関数が有理の場合、必要な計算は前出の段落に記載された考慮事項に基づいています。
コマンド r = rsmak(shape) は、'circle'、'arc'、'cylinder'、'sphere'、'cone'、'torus' などの特定の標準の幾何学的形状を正確に記述する rB 型の有理スプラインを提供します。コマンド fncmb(r,trans) を使用して、結果の形状に標準の変換を適用できます。たとえば、trans が正しい長さの列ベクトルの場合、形状はそのベクトルによって変換されますが、trans が回転などの適切な行列の場合は、形状はその行列によって変換されます。
コマンド r = rscvn(p) は、平面状の点の特定のシーケンス p を通過し、円弧で構成された 2 次 rB 型の接線連続曲線を作成します。
NURBS と呼ばれる特殊な有理スプライン型は、CAGD における標準ツールとなっています。NURBS は、定義では、s と w の両方が同じ B 型の有理スプラインで、s の各係数は w の対応する係数を因子として明示的に含んでいます。
分子スプラインの正規化された係数 a(:,i) は、rB 型で使用されている非正規化係数 v(i)a(:,i) より、制御点としてより容易に使用できます。しかしながら、このツールボックスは特殊な NURBS 型は提供しておらず、より一般的な有理スプラインのみを B 型 (内部では rBform と呼ばれる) と pp 型 (内部では rpform と呼ばれる) の両方で提供しています。
以前に使用されていた有理スプライン circle は、次のようなコードによって rsmak に組み込まれています。
x = [1 1 0 -1 -1 -1 0 1 1]; y = [0 1 1 1 0 -1 -1 -1 0]; s45 = 1/sqrt(2); w =[1 s45 1 s45 1 s45 1 s45 1]; circle = rsmak(augknt(0:4,3,2), [w.*x;w.*y;w]);
最後の成分としての分母スプラインが出現していることに注意してください。また、分母スプラインの係数が、分子スプラインの対応する係数の因子として、ここでどのように明示的に出現するかにも注意してください。正規化された係数シーケンス [x;y] は非常にシンプルです。適切な順序で "単位正方形" の頂点と中間点から構成されています。生成される制御多角形は、円を形成する 4 つの 2 次区分が接する場所で、円に対する正接となります。
NURBS の詳細については、[G. Farin, NURBS, 2nd ed., AKPeters Ltd, 1999] または [Les Piegl and Wayne Tiller, The NURBS Book, 2nd ed., Springer-Verlag, 1997] を参照してください。