pp 型スプラインの作成と操作

pp 型の作成

区分的多項式は、通常、何らかのコマンドによって、内挿または近似のプロセスを通じて、または一部の他の形式 (B 型など) からの変換によって作成され、変数として出力されます。ただし、ステートメントを使用してゼロから構成することもできます。

pp
= ppmak(breaks,coefs)

たとえば、pp=ppmak(-5:-1,-22:-11) を入力するとします。より明確には、以下を入力した場合、

breaks = -5:-1;
coefs = -22:-11; pp = ppmak(breaks,coefs);

一様のブレークシーケンス -5:-1 と係数シーケンス -22:-11 を指定します。このブレークシーケンスは 5 エントリであるため、4 つのブレーク区間があり、係数シーケンスは 12 エントリであるため、実際には、次数 3 (= 12/4) の区分的多項式を指定したことになります。以下のコマンドを入力します。

fnbrk(pp)

次のようにこの区分的多項式のすべての構成要素が出力されます。

breaks(1:l+1)
    -5 -4 -3 -2 -1  
coefficients(d*l,k)
     -22 -21 -20
     -19 -18 -17
     -16 -15 -14 
     -13 -12 -11
  pieces number l
    4 
order k 
  3 
dimension d of target
    1

さらに、fnbrk を使用すると、これらの各構成要素を個別に指定できます。ただし、Curve Fitting Toolbox™ スプライン機能では、通常、これらの詳細を指定する必要はありません。pp をコマンドの引数として使用するだけで、区分的多項式の評価、微分、積分、変換またはプロットを行うことができます。詳細については、pp を参照してください。

pp 型スプラインの操作

以下に、区分的多項式で実行できる操作用の関数をいくつか示します。

`v = fnval(pp,x)`	評価する
`dpp = fnder(pp)`	微分
`dirpp = fndir(pp,dir)`	`dir` 方向に微分する
`ipp = fnint(pp)`	積分する
`fnmin(pp,[a,b])`	指定した区間での最小値を求める
`fnzeros(pp,[a,b])`	指定した区間での 0 を求める
`pj = fnbrk(pp,j)`	`j` 番目の多項式区分を示す
`pc = fnbrk(pp,[a b])`	区間 [`a`..`b`] に制限/拡張する
`po = fnxtr(pp,order)`	指定された次数の多項式により基本区間外に拡張する
`fnplt(pp,[a,b])`	与えられた区間でプロットする
`sp = fn2fm(pp,'B-')`	B 型に変換する
`pr = fnrfn(pp,morebreaks)`	追加のブレークを挿入する

追加のブレークを挿入すると、コマンド fncmb のように、異なるブレークをもつ 2 つの区分的多項式を追加する場合に役立ちます。

pp 型の例

pp 型の作成で説明した特定の区分的多項式 (pp 型) を作成し、プロットするには、以下のコマンドを実行します。

ブレークシーケンス -5:-1 と係数シーケンス -22:-11 をもつ区分的多項式を作成します。
```
pp=ppmak(-5:-1,-22:-11)
```

基本プロットを作成します。

x = linspace(-5.5,-.5,101);
plot(x, fnval(pp,x),'x')

プロットにブレーク線を追加します。

breaks=fnbrk(pp,'b'); yy=axis; hold on
for j=1:fnbrk(pp,'l')+1
   plot(breaks([j j]),yy(3:4))
end

3 番目の多項式区分を提供する多項式のプロットを重ね合わせます。
```
plot(x,fnval(fnbrk(pp,3),x),'linew',1.3)
set(gca,'ylim',[-60 -10]), hold off 
```

区分的多項式関数、そのブレーク、およびその 3 番目の区分を提供する多項式

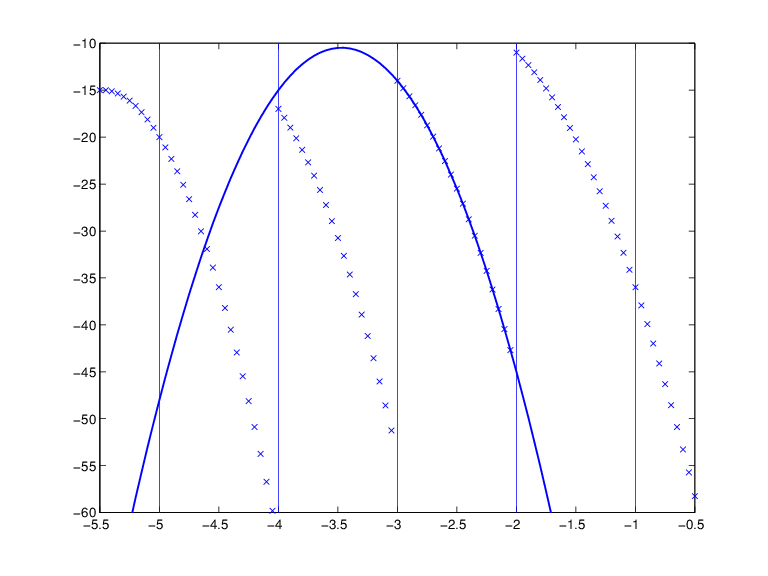
The plot shows a concave down parabola and five vertical lines. Between each pair of vertical lines, a different segment of the parabola is plotted with crosses.

上の Figure は最終の図です。区分的多項式は点のシーケンスとして示され、その最上位から連続して、3 番目の多項式区分の取得元となる多項式が示されています。ブレークの区分的多項式の値が "右" からの極限であり、基本区間外の区分的多項式の値はそれぞれ多項式区分の左端、右端を拡張することで取得されていることは明らかです。

pp 型の区分的多項式により効率的に評価できますが、通常は、最初に "B 型"、つまり B スプラインの線形結合の表現を決定することで、あるデータからの区分的多項式の "作成" はより効率的に処理されます。