テンソル積スプラインによる近似
ツールボックスは "ベクトル" 係数と共にスプラインを処理できるため、以降の説明でわかるように、テンソル積スプラインによるグリッド データへの内挿または近似の実装は容易です。また、"二変量テンソル積スプライン" の例を実行できます。
確かに、グリッド データへのテンソル積スプライン近似のほとんどは、この例で説明する詳細を考慮することなく、このツールボックスの spapi や csape などのスプライン作成コマンドのいずれかを使用して直接取得できます。むしろ、この例はテンソル積作成の背後にある理論を示すための手段であり、このツールボックスの作成コマンドが対応していない状況で役立ちます。
このセクションでは、テンソル積スプラインの問題の次の点について説明します。
サイトとノットの選択
たとえば、与えられたデータ z(i,j)=f(x(i),y(j)),i=1:Nx,j=1:Ny への最小二乗近似を考えてみます。曲面近似のスキーマをテストするためのフランケによって広く使用されている関数からデータを取得します (R. Franke, "A critical comparison of some methods for interpolation of scattered data", Naval Postgraduate School Techn. Rep. NPS-53-79-003, March 1979 を参照)。領域は単位正方形です。y 方向よりも、x 方向で少し多くデータ サイトを選択します。また、より明確に定義するには、境界の近くでデータ密度が高くなるようにします。
x = sort([(0:10)/10,.03 .07, .93 .97]); y = sort([(0:6)/6,.03 .07, .93 .97]); [xx,yy] = ndgrid(x,y); z = franke(xx,yy);
y の関数としての最小二乗近似
これらのデータは、ベクトル値関数、つまり、y(j) における値がベクトル z(:,j) (すべての j について) になる関数 y から得られたデータとして扱います。特に理由はありませんが、この関数を、等間隔の 3 つの内部ノットをもつベクトル値放物線スプラインによって近似することを選択してください。つまり、このベクトル値スプラインのスプラインの次数とノット シーケンスを次のように選択します。
ky = 3; knotsy = augknt([0,.25,.5,.75,1],ky);
その後、spap2 を使用して、データへの最小二乗近似を提供します。
sp = spap2(knotsy,ky,y,z);
実際には、Sky,knotsy から各 Nx データ セットへの離散最小二乗近似を同時に求めていることになります。
特に、ステートメント
yy = -.1:.05:1.1; vals = fnval(sp,yy);
は、配列 vals を提供します。この配列のエントリ vals(i,j) はメッシュポイント x(i),yy(j) における基礎関数 f の値 f(x(i),yy(j)) と見なすことができます。これは、vals(:,j) が、sp での近似スプライン曲線の yy(j) における値であるためです。
これは、次のコマンドで取得される以下の Figure で明らかです。
mesh(x,yy,vals.'), view(150,50)
mesh コマンドで vals.' を使用している点に注意してください。配列をプロットする際の MATLAB® 行列指向の表示であるため必要となります。これは、二変量近似で深刻な問題となることがあります。なぜなら、一般的に z(i, j) は点 (x(i), y(j)) における関数値として見なされますが、MATLAB では z(i, j) を、点 (x(j), y(i)) における関数値と見なすためです。
曲面のように見える一連の滑らかな曲線
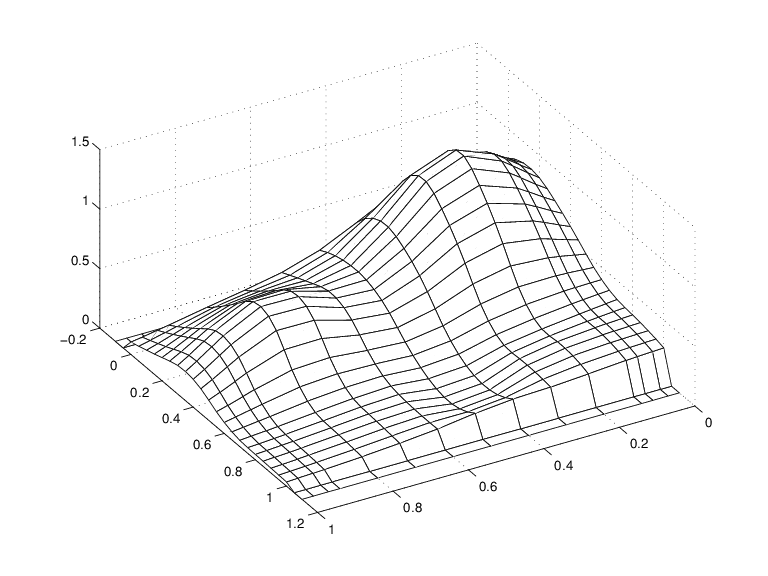
それぞれの滑らかな曲線の最初の 2 つの値と最後の 2 つの値は実際には 0 である点に注意してください。これは、yy の最初の 2 つのサイトと最後の 2 つのサイトがどちらも、sp 型スプラインの基本区間外であるためです。
また、リッジにも注意してください。これで、滑らかな曲線が一方向のみでプロットされていることが確認できます。
x の関数としての係数への近似
実際の曲面を得るには、さらに 1 ステップを実行する必要があります。以下は、sp のスプラインの係数 coefsy です。
coefsy = fnbrk(sp,'coefs');
抽象的に、sp のスプラインは関数として考えることができます。
ベクトル係数 coefsy(:,r) の i 番目のエントリ coefsy(i,r) は x(i) (すべての i について) に対応します。これは、同じ次数 kx および同じ適切なノット シーケンス knotsx のスプラインによる各係数ベクトル coefsy(q,:) の近似を示しています。特に理由はありませんが、今回は等間隔の "4" つの内部ノットをもつ "3 次" スプラインを使用します。
kx = 4; knotsx = augknt([0:.2:1],kx); sp2 = spap2(knotsx,kx,x,coefsy.');
spap2(knots,k,x,fx) は、fx(:,j) が x(j) におけるデータとなると想定している点に注意してください。つまり、fx の各 "列" が関数値になると想定しています。x(q) (すべての q について) におけるデータ coefsy(q, :) に当てはめるには、coefsy の "転置" と共に spap2 を提供します。
二変量近似
ここでは、得られたスプライン "曲線" の係数 cxy の転置について検討します。
coefs = fnbrk(sp2,'coefs').';
以下の "二変量" スプライン近似が提供されます。
元のデータは、以下のとおりです。
このスプライン曲面をグリッド (以下に例を示します) 上にプロットするために
xv = 0:.025:1; yv = 0:.025:1;
以下を実行できます。
values = spcol(knotsx,kx,xv)*coefs*spcol(knotsy,ky,yv).'; mesh(xv,yv,values.'), view(150,50);
これにより以下の Figure が得られます。
フランケ関数へのスプライン近似

これは有意義です。なぜなら、spcol(knotsx,kx,xv) が行列であり、この行列の (i,q) 番目のエントリが、ノット シーケンス knotsx では、次数 kx の q 番目の B スプラインの xv(i) における値 Bq,kx(xv(i)) に等しいためです。
行列 spcol(knotsx,kx,xv) と spcol(knotsy,ky,yv) は帯状のため、次のように "大きな" xv と yv の場合に fnval を使用すると、効率が向上する場合がありますが、おそらくメモリ消費量が増加します。
value2 = ... fnval(spmak(knotsx,fnval(spmak(knotsy,coefs),yv).'),xv).';
これは実際に、以下のように fnval がテンソル積スプラインによって直接呼び出されたときに、内部で起こっていることです。
value2 = fnval(spmak({knotsx,knotsy},coefs),{xv,yv});
以下は、相対誤差の計算です。相対誤差とは、与えられたデータの大きさを基準とする、与えられたデータとそれらデータ サイトでの近似の値との差です。
errors = z - spcol(knotsx,kx,x)*coefs*spcol(knotsy,ky,y).'; disp( max(max(abs(errors)))/max(max(abs(z))) )
出力は 0.0539 で、おそらくそれほど大きいわけではありません。ただし、係数配列はサイズ 8 6 のみでした。
disp(size(coefs))
サイズ 15 11 のデータ配列を近似するには、次のようになります。
disp(size(z))
次数の切り替え
ここで従うアプローチは、次のように "偏っている" ように見えます。まず、与えられたデータ z を y のベクトル値関数を記述しているものと考え、その後、近似曲線のベクトル係数によって形成される行列を x のベクトル値関数を記述しているものとして扱います。
逆の順序で考えた場合、つまり、z を x のベクトル値関数を記述するものと考え、その後、近似曲線のベクトル係数から構成される行列を y のベクトル値関数を記述するものとして扱うと、何が起こるでしょうか。
驚くかもしれませんが、最終近似は同じ (丸めを除く) になります。ここでは数値実験を行います。
x の関数としての最小二乗近似
最初にスプライン曲線をデータに近似しますが、今回は、x を独立変数として使用するため、データ値になるのは z の "行" です。それに応じて、z ではなく、z.' を spap2 に提供しなければなりません。
spb = spap2(knotsx,kx,x,z.');
これで、すべての曲線 (x ; z (:, j)) へのスプライン近似が得られます。特に、ステートメント
valsb = fnval(spb,xv).';
は、行列 valsb を提供します。この行列のエントリ valsb(i, j) は、メッシュポイント (xv(i),y(j)) における基礎関数 f の値 f(xv(i),y(j)) への近似と見なすことができます。これは、mesh を使用して valsb をプロットする場合に明らかです。
mesh(xv,y,valsb.'), view(150,50)
曲面のように見える別の一連の滑らかな曲線
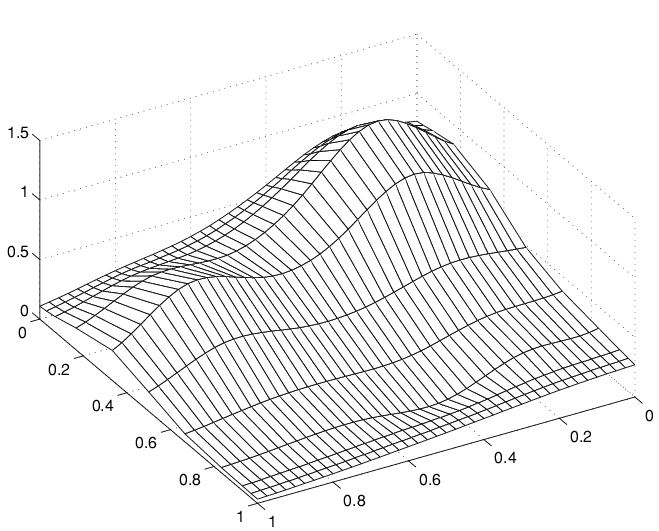
リッジに注意してください。これで、やはり、滑らかな曲線が一方向のみでプロットされていることが確認できます。ただし、今回は、曲線が逆方向に向かっています。
y の関数としての係数への近似
ここで 2 番目のステップで、実際の曲面を取得します。まず、係数を抽出します。
coefsx = fnbrk(spb,'coefs');
その後、同じ次数 ky および適切な同じノット シーケンス knotsy のスプラインによって各係数ベクトル coefsx(r,:) に当てはめます。
spb2 = spap2(knotsy,ky,y,coefsx.');
ここでも、spb からの係数配列を転置する必要がある点に注意してください。これは、spap2 が最終入力引数の列をデータ値として使用するためです。
それに応じて、得られた "曲線" の係数配列 coefsb を転置する必要がなくなります。
coefsb = fnbrk(spb2,'coefs');
二変量近似
coefsb は前出の係数配列 coefs と等しい (丸めを除く) と主張されています。以下はテストです。
disp( max(max(abs(coefs - coefsb))) )
出力は 1.4433e-15 です。
説明は簡単です。sp = spap2(knots,k,x,y) に含まれるスプライン s の係数 c は、入力値 y に "線形" に依存します。これは、c と y が両方とも 1 行の行列の場合に、A=Aknots,k,x のような行列が存在することを意味します。これにより、
が、任意のデータ y で成り立ちます。このステートメントは y が "行列" でサイズが d 行 N 列などの場合でも成り立ちます。この場合は、各データ y(:,j) が Rd 内の点と見なされ、得られたスプラインは、それに応じて d ベクトル値となります。したがって、係数配列 c はサイズ d 行n 列 (n = length(knots)-k) となります。
特に、ステートメント
sp = spap2(knotsy,ky,y,z); coefsy =fnbrk(sp,'coefs');
は、次を満たす行列 coefsy を提供します。
後続の計算
sp2 = spap2(knotsx,kx,x,coefsy.'); coefs = fnbrk(sp2,'coefs').';
によって係数配列 coefs が生成されます。この配列は 2 つの転置を考慮して次を満たします。
代替の 2 番目の計算では、最初に次を計算しました。
spb = spap2(knotsx,kx,x,z.'); coefsx = fnbrk(spb,'coefs');
そのため、coefsx=z'.Aknotsx,kx,x です。後続の計算
spb2 = spap2(knotsy,ky,y,coefsx.'); coefsb = fnbrk(spb,'coefs');
によって次が提供されます。
その結果、coefsb = coefs となります。
比較と拡張
2 番目のアプローチは、spap2 が呼び出されるたびに転置が実行され、ほかでは実行されないという点で、1 番目のアプローチより対称的です。このアプローチは、任意の数の変数でグリッド データに近似するために使用できます。
たとえば、"3" 次元グリッド上の特定のデータが、サイズ [Nx,Ny,Nz] の 3 次元配列 v に含まれ、v(i,j,k) が値 f(x(i),y(j),z(k)) を含む場合は、次から開始します。
coefs = reshape(v,Nx,Ny*Nz);
nj = knotsj - kj (j = x,y,z の場合) と仮定して、次のように進めます。
sp = spap2(knotsx,kx,x,coefs.'); coefs = reshape(fnbrk(sp,'coefs'),Ny,Nz*nx); sp = spap2(knotsy,ky,y,coefs.'); coefs = reshape(fnbrk(sp,'coefs'),Nz,nx*ny); sp = spap2(knotsz,kz,z,coefs.'); coefs = reshape(fnbrk(sp,'coefs'),nx,ny*nz);
詳細については、PGS の第 17 章または [C. de Boor, "Efficient computer manipulation of tensor products," ACM Trans.Math.Software 5 (1979), 173–182; Corrigenda, 525] を参照してください。同じ参考文献により、最小二乗近似の使用について、ここでは特に特別なことがないことも明らかです。得られる近似が特定のデータに線形に依存する係数をもつ近似プロセス (スプライン内挿を含む) はいずれも、同じ方法で、グリッド データへの多変量近似プロセスに拡張できます。
これはまさに、グリッド データを近似する際に、スプライン作成コマンド csapi、csape、spapi、spaps、および spap2 で使用されている方法です。また、テンソル積スプラインがグリッド上で評価されるときに、fnval でも使用されます。