熱交換器での温度制御

この例では、フィードバック補償器およびフィードフォワード補償器を設計し、熱交換器により化学反応器の温度を調整する方法を示します。

熱交換器のプロセス

以下に、"攪拌タンク" と呼ばれる化学反応器を示しています。上部の入口からは、水槽内で混合する液体が送られます。水槽の液体は、制御バルブを経由して熱交換器 (下部のパイプ) に供給される流量を調節することで、一定の温度を維持しなければなりません。入口の流れの温度の変動は、このプロセスの外乱の主な原因となります。

測定データを使用した熱交換器ダイナミクスのモデル化

デッドタイムを付加した 1 次モデルを熱交換器の特性から導出するには、バルブ電圧 V にステップ外乱を加え、水槽の温度 T に対する影響を時間経過に沿って記録します。実験データを読み込んでプロットします。

load("step_data.mat","tData","yData")

plot(tData,yData,"r*-")
xlim([0 200])
ylim([0 1.2])
ylabel("Tank temperature (normalized)")
xlabel ("Time (seconds)")
grid on;
title("Measured Step Response");

hold on
t1 = 23;
t2 = 36;
plot([t1 t1],[0 0.283],"b--",LineWidth=2)
plot([0 t1],[0.283 0.283],"b--",LineWidth=2)
annotation("textbox",[0.22 0.26 0.1 0.1], ...
    String="t1",Color="b",EdgeColor="none")
plot([t2 t2],[0 0.632],"b--",LineWidth=2)
plot([0 t2],[0.632 0.632],"b--",LineWidth=2)
annotation("textbox",[0.28 0.48 0.1 0.1], ...
    String="t2",Color="b",EdgeColor="none")

Figure contains an axes object. The axes object with title Measured Step Response, xlabel Time (seconds), ylabel Tank temperature (normalized) contains 5 objects of type line.

値 t1 および t2 は、応答が最終値の 28.3% および 63.2% に到達した時間です。これらの値を使用すると、熱交換器の時定数 tau とデッドタイム theta を推定できます。

tau = 3/2 * ( t2 - t1 )

tau = 
19.5000

theta = t2 - tau

theta = 
16.5000

デッドタイムを付加した 1 次応答を測定した応答と比較して、これらの計算を検証します。

s = tf("s");
Gp = exp(-theta*s)/(1+tau*s);

Gp のステップ応答を実験データと同じ座標軸上にプロットします。

sp = stepplot(Gp,0:1:200);
xlim([0 200])
ylim([0 1.2])
ylabel("Tank temperature (normalized)")
title("Experimental and Simulated Step Response")
grid on

MATLAB figure

モデル応答と実験データは非常によく一致しています。流入温度のステップ外乱に対する 1 次応答を推定するには、似たようなバンプテスト実験を実施できます。熱交換器と流入外乱に対するモデルを用意したので、これで制御アルゴリズムを設計する準備が整いました。

フィードバック制御

次の図は開ループプロセスのブロック線図を示しています。

次の伝達関数

$G_{p} (s) = \frac{e^{- 14.7 s}}{21.3 s + 1}$

は、蒸気バルブを開く電圧 V の変化が水槽の温度 T にどのように影響を及ぼすかをモデル化したもので、次の伝達関数

$G_{d} (s) = \frac{e^{- 35 s}}{25 s + 1}$

は、流入温度の変化 d が T に及ぼす影響をモデル化したものです。与えられた設定点 Tsp 付近の水槽の温度 T を調節するには、次のフィードバックアーキテクチャを使用してバルブの開口 (電圧 V) を制御できます。

この設定では、比例積分 (PI) コントローラー

$C (s) = K_{c} (1 + \frac{1}{τ_{c} s})$

が、望ましい温度と測定温度間のギャップ Tsp-T に基づいて電圧 V を計算します。コントローラーのパラメーターに適した値を選択するには、ITAE 式を使用できます。

$K_{c} = 0.859 (θ / τ)^{- 0.977}, τ_{c} = (θ / τ)^{0.680} τ / 0.674$

Kc = 0.859 * (theta / tau)^(-0.977)

Kc = 
1.0113

tauc = ( tau / 0.674 ) * ( theta / tau )^0.680

tauc = 
25.8250

C = Kc * (1 + 1/(tauc*s));

ITAE コントローラーの動作を確認するには、フィードバックループを閉じ、設定点の変化に対する応答をシミュレートします。

figure
Tfb = feedback(ss(Gp*C),1);
stepplot(Tfb,0:1:200)
hold on
plot(tData,yData,"r*-")
title("Response to Step Change in Temperature Setpoint")
ylabel("Tank temperature (normalized)")
grid on

MATLAB figure

応答は比較的速く、一部にオーバーシュートが見られます。安定余裕を見てみると、ゲイン余裕が弱いことがわかります。

figure
margin(Gp*C)
grid on

MATLAB figure

比例ゲイン Kc を減らすと性能は低下しますが、安定性は強化されます。

C1 = 0.9 * (1 + 1/(tauc*s));  % reduce Kc from 1.23 to 0.9
margin(Gp*C1)
grid on

MATLAB figure

figure
stepplot(Tfb,"r",feedback(ss(Gp*C1),1),"b",0:1:200)
title("Response to Step Change in Temperature Setpoint")
ylabel("Tank temperature (normalized)")
legend("Kc = 1.23","Kc = 0.9");
grid on

MATLAB figure

フィードフォワード制御

流入温度の変化は水槽内の温度が変動する主な原因であることを思い出してください。このような外乱を避けるために、フィードバック制御に代わるものとして、以下に示すフィードフォワードアーキテクチャがあります。

この構成では、フィードフォワードコントローラー F は流入温度の測定値を使用して蒸気バルブの開口 (電圧 V) を調整します。したがって、フィードフォワード制御では流入温度の変化の影響を予期し、事前に回避します。

簡単な計算により、温度の外乱 d は水槽の温度 T に次のように総合的に伝達されることが示されます。

$T = (G_{p} F + G_{d}) d$

完全に外乱を抑制するには以下が必要です。

$G_{p} F + G_{d} = 0 \to F = - \frac{G_{d}}{G_{p}} = - \frac{21.3 s + 1}{25 s + 1} e^{- 20.3 s}$

実際には、モデル化が不正確であると外乱を正確に抑制できなくなりますが、フィードフォワード制御を行うと、流入外乱による温度の変動を最小限に抑えることができます。フィードフォワード方法がどのように機能するかを詳しく理解するには、理想的なフィードフォワードの遅れを 5 秒増加し、流入温度のステップ変化に対する応答をシミュレートします。

Gd = exp(-35*s)/(25*s+1);
F = -(21.3*s+1)/(25*s+1) * exp(-25*s);
Tff = Gp * ss(F) + Gd;   % d->T transfer with feedforward control

figure
stepplot(Tff)
title("Effect of Step Disturbance in Inflow Temperature")
ylabel("Tank temperature (normalized)")
grid on

MATLAB figure

フィードフォワード/フィードバック結合型制御

フィードバック制御は一般的に設定点の追従に適しています。一方、フィードフォワード制御は測定された外乱の抑制に役立ちます。次に、両方の方法を組み合わせることの利点を見ていきます。対応する制御アーキテクチャを次の図に示します。

connect を使用して、Tsp,d から T への対応する閉ループモデルを作成します。まず、各ブロックの入力チャネルと出力チャネルに名前を付け、次に connect を使用してブロック線図の線をつなぎます。

Gd.u = "d";
Gd.y = "Td";
Gp.u = "V";
Gp.y = "Tp";
F.u = "d";
F.y = "Vf";
C.u = "e";
C.y = "Vc";
Sum1 = sumblk("e = Tsp - T");
Sum2 = sumblk("V = Vf + Vc");
Sum3 = sumblk("T = Tp + Td");
Tffb = connect(Gp,Gd,C,F,Sum1,Sum2,Sum3,{"Tsp","d"},"T");

フィードフォワード制御を使用した閉ループ応答と使用しない閉ループ応答を比較するために、フィードバックのみの設定に対し、対応する閉ループ伝達関数を計算します。

C.u = "e";
C.y = "V";
Tfb = connect(Gp,Gd,C,Sum1,Sum3,{"Tsp","d"},"T");

2 つの設計を比較します。

stepplot(Tfb,"b",Tffb,"r--");
title("Closed-loop Step Response to Setpoint and Disturbance Change");
ylabel("Tank temperature (normalized)")
legend("Feedback only","Feedforward + feedback");
grid on

MATLAB figure

設定点の追従性能は 2 つの設計で同じですが、フィードフォワード制御を追加すると外乱の抑制が向上します。この結果は、閉ループボード線図を見ても明確です。

figure
bodemag(Tfb,"b",Tffb,"r--",{1e-3,1e1})
legend("Feedback only","Feedforward + feedback",Location="SouthEast");

MATLAB figure

対話型シミュレーション

HeatExchanger アプリを使用して、熱交換器システムの制御戦略を対話的に調べることができます。このアプリは App Designer を使用して開発されたものであり、heatex_sim Simulink® モデルを使用して熱交換器をシミュレートします。

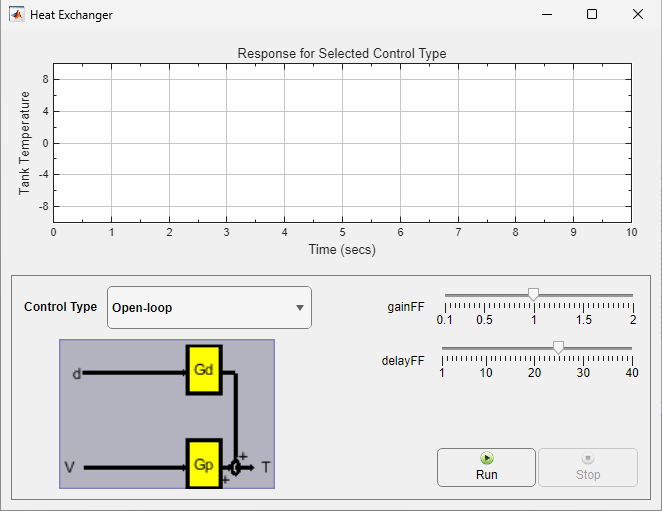
このアプリを使用すると、開ループ、フィードフォワード、フィードバック、およびフィードフォワード/フィードバック結合型制御を使用して熱交換器をシミュレートできます。フィードフォワードコントローラーのゲインと遅延のパラメーターを調整することもできます。

アプリを実行するには次のコマンドを使用します。

HeatExchanger