設定点の追従と外乱の抑制の PID 調整
この例では、systune を使用して、PID コントローラーを調整する際の設定点の追従と外乱の抑制間におけるトレードオフを調べます。
PID 調整のトレードオフ
1-DOF PID コントローラーを調整する場合は、適切な追従と迅速な外乱の抑制を同時に実現できないことがよくあります。制御帯域幅が固定されていると仮定すると、外乱の抑制を迅速化するためには帯域幅内により多くのゲインが必要です。これは、交差周波数に近い傾きを増やすことでのみ実現できます。傾きが大きくなることは位相余裕が小さくなることを意味するため、通常は設定点の変化に対する応答でオーバーシュートが増えます。

図 1: 1-DOF PID 調整でのトレードオフ。
この例では、systune を使用してこのトレードオフを調べ、アプリケーションに適した妥協点を見つけます。このようなトレードオフは PID 調整器アプリでも可能です。詳細については、設定値追従と外乱の抑制のいずれかを優先するための PID コントローラーの調整 (PID 調整器)を参照してください。
調整の設定
プラント入力に負荷外乱がある図 2 の PID ループについて考えます。

図 2: PID 制御ループ
この例では、プラント モデルを使用します。
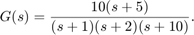
ターゲットの制御帯域幅は 10 rad/s です。調整可能な PID コントローラーを作成し、その微分フィルター時定数を  (帯域幅の 10 倍) に設定して、3 つのゲイン (比例ゲイン、積分ゲイン、微分ゲイン) のみを調整するようにします。
(帯域幅の 10 倍) に設定して、3 つのゲイン (比例ゲイン、積分ゲイン、微分ゲイン) のみを調整するようにします。
G = zpk(-5,[-1 -2 -10],10); C = tunablePID('C','pid'); C.Tf.Value = 0.01; C.Tf.Free = false; % fix Tf=0.01
r から y への閉ループ伝達の調整可能なモデル T0 を構成します。"解析ポイント" ブロックを使用して、外乱が入る位置 u をマークします。
LS = AnalysisPoint('u'); T0 = feedback(G*LS*C,1); T0.u = 'r'; T0.y = 'y';
開ループ応答 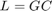 のゲインは、フィードバック ループ動作の重要なインジケーターです。開ループ ゲインは、良好な外乱の抑制を実現するためには制御帯域幅内で高い値 (1 を超える) でなければならず、測定ノイズとモデル化されていないプラント ダイナミクスの影響を受けないようにするには制御帯域幅外では低い値 (1 未満) でなければなりません。したがって、次の 3 つの要件を使用して制御目的を表します。
のゲインは、フィードバック ループ動作の重要なインジケーターです。開ループ ゲインは、良好な外乱の抑制を実現するためには制御帯域幅内で高い値 (1 を超える) でなければならず、測定ノイズとモデル化されていないプラント ダイナミクスの影響を受けないようにするには制御帯域幅外では低い値 (1 未満) でなければなりません。したがって、次の 3 つの要件を使用して制御目的を表します。
rでのステップ変化に対する約 0.2 秒の応答時間を指定する "Tracking" 要件交差周波数 10 rad/s を超えて -20 dB/decade のロールオフを強制する "MaxLoopGain" 要件
0.1 rad/s を下回る周波数で積分ゲインを調整する "MinLoopGain" 要件
s = tf('s'); wc = 10; % target crossover frequency % Tracking R1 = TuningGoal.Tracking('r','y',2/wc); % Bandwidth and roll-off R2 = TuningGoal.MaxLoopGain('u',wc/s); % Disturbance rejection R3 = TuningGoal.MinLoopGain('u',wc/s); R3.Focus = [0 0.1];
1-DOF PID コントローラーの調整
systune を使用して、これらの要件に合うように PID ゲインを調整します。帯域幅と外乱の抑制の目標を厳密な制約として扱い、これらの制約に従って追従を最適化します。
T1 = systune(T0,R1,[R2 R3]);
Final: Soft = 1.12, Hard = 0.99979, Iterations = 156
3 つのすべての要件がほぼ満たされていることを確認します。青い曲線は達成した値、黄色の部分は要件に違反している領域を強調表示しています。
figure('Position',[100,100,560,580])
viewGoal([R1 R2 R3],T1)

追従と抑制
追従と外乱の抑制間のトレードオフの詳細を得るには、周波数帯域 [0,0.1] rad/s 内の最小ループ ゲインを  倍に増やします。値
倍に増やします。値 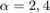 に対して PID ゲインを再調整します。
に対して PID ゲインを再調整します。
% Increase loop gain by factor 2
alpha = 2;
R3.MinGain = alpha*wc/s;
T2 = systune(T0,R1,[R2 R3]);
Final: Soft = 1.17, Hard = 0.99954, Iterations = 115
% Increase loop gain by factor 4
alpha = 4;
R3.MinGain = alpha*wc/s;
T3 = systune(T0,R1,[R2 R3]);
Final: Soft = 1.25, Hard = 0.99994, Iterations = 166
ステップ コマンド r に対する応答を、プラント入力 u で入るステップ外乱 d に対する応答と比較します。
figure, step(T1,T2,T3,3) title('Setpoint tracking') legend('\alpha = 1','\alpha = 2','\alpha = 4')

% Compute closed-loop transfer from u to y D1 = getIOTransfer(T1,'u','y'); D2 = getIOTransfer(T2,'u','y'); D3 = getIOTransfer(T3,'u','y'); step(D1,D2,D3,10) title('Disturbance rejection') legend('\alpha = 1','\alpha = 2','\alpha = 4')

alpha の増加とともに外乱の抑制は改善されますが、設定点の追従のオーバーシュートは大きくなることに注意してください。3 つの設計の開ループ応答をプロットし、alpha により交差 (0 dB) の前の傾きがいかに増えるかに注目します。
L1 = getLoopTransfer(T1,'u'); L2 = getLoopTransfer(T2,'u'); L3 = getLoopTransfer(T3,'u'); bodemag(L1,L2,L3,{1e-2,1e2}), grid title('Open-loop response') legend('\alpha = 1','\alpha = 2','\alpha = 4')
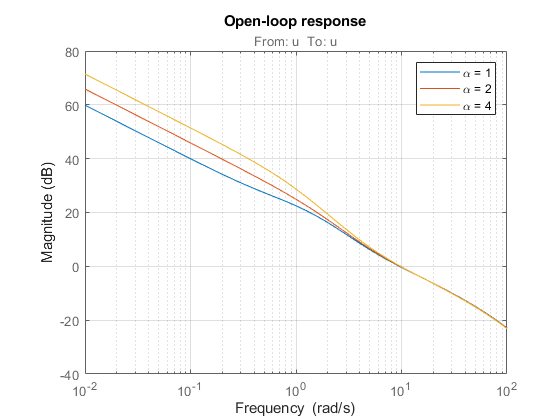
最適な設計は、調整しているフィードバック ループの主要な目的によって異なります。
2-DOF PID コントローラーの調整
追従を低下させてまで外乱の抑制を向上させることができない場合は、代わりに 2-DOF アーキテクチャの使用を検討してください。2-DOF PID コントローラーでは、外乱の抑制を、設定点の追従におけるオーバーシュートを大きく増加させることなく迅速に実行できます。
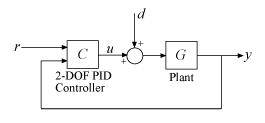
図 3: 2-DOF PID 制御ループ
tunablePID2 オブジェクトを使用して 2-DOF PID コントローラーをパラメーター化し、図 3 の閉ループ システムの調整可能なモデル T0 を構成します。
C = tunablePID2('C','pid'); C.Tf.Value = 0.01; C.Tf.Free = false; % fix Tf=0.01 T0 = feedback(G*LS*C,1,2,1,+1); T0 = T0(:,1); T0.u = 'r'; T0.y = 'y';
次に、前に試した最大ループ ゲイン (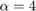 ) 用に 2-DOF PI コントローラーを調整します。
) 用に 2-DOF PI コントローラーを調整します。
% Minimum loop gain inside bandwidth (for disturbance rejection) alpha = 4; R3.MinGain = alpha*wc/s; % Tune 2-DOF PI controller T4 = systune(T0,R1,[R2 R3]);
Final: Soft = 1.09, Hard = 0.81139, Iterations = 78
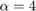 に対する 1-DOF 設計および 2-DOF 設計の設定点の追従プロパティと外乱の抑制プロパティを比較します。
に対する 1-DOF 設計および 2-DOF 設計の設定点の追従プロパティと外乱の抑制プロパティを比較します。
clf, step(T3,'b',T4,'g--',4) title('Setpoint tracking') legend('1-DOF','2-DOF')

D4 = getIOTransfer(T4,'u','y'); step(D3,'b',D4,'g--',4) title('Disturbance rejection') legend('1-DOF','2-DOF')
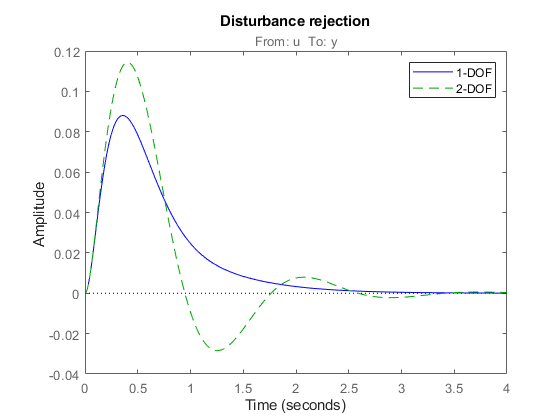
ステップ外乱への応答は似ていますが、2-DOF コントローラーでは設定点の変化への応答でオーバーシュートが除去されます。showTunable を使用して 1-DOF コントローラーと 2-DOF コントローラーの調整されたゲインを比較できます。
showTunable(T3) % 1-DOF PI
C =
1 s
Kp + Ki * --- + Kd * --------
s Tf*s+1
with Kp = 9.51, Ki = 14.9, Kd = 0.89, Tf = 0.01
Name: C
Continuous-time PIDF controller in parallel form.
showTunable(T4) % 2-DOF PI
C =
1 s
u = Kp (b*r-y) + Ki --- (r-y) + Kd -------- (c*r-y)
s Tf*s+1
with Kp = 5.25, Ki = 20, Kd = 0.799, Tf = 0.01, b = 0.66, c = 1.38
Name: C
Continuous-time 2-DOF PIDF controller in parallel form.