このページは機械翻訳を使用して翻訳されました。最新版の英語を参照するには、ここをクリックします。
飛行データのG力を推定する
この例では、飛行データを読み込み、飛行中の G 力を推定する方法を示します。
記録された飛行データを分析用に読み込む
記録されたデータには、次の飛行パラメータが含まれます。
迎え角(アルファ)(ラジアン)
横滑り角(ベータ)(ラジアン)
指示対気速度(IAS)(ノット)
体の角速度(オメガ)ラジアン/秒、
ダウンレンジとクロスレンジの位置(フィート単位)
高度(alt)をフィートで表します。
load('astflight.mat');読み込まれたデータから飛行パラメータを抽出する
記録されたデータから、迎え角 (アルファ)、横滑り角 (ベータ)、機体角速度 (オメガ)、高度 (alt) の MATLAB ® 変数が作成されます。convangvel 関数は、体の角速度をラジアン/秒 (rad/s) から度/秒 (deg/s) に変換するために使用されます。
alpha = fltdata(:,2); beta = fltdata(:,3); omega = convangvel( fltdata(:,5:7), 'rad/s', 'deg/s' ); alt = fltdata(:,10);
指示対気速度から真対気速度を計算する
この飛行データセットには、示対気速度 (IAS) が記録されています。指示対気速度(IAS)はコックピットの計器に表示されます。計算を実行するには、通常、測定誤差のない対気速度である真対気速度 (TAS) が使用されます。
測定誤差は、対気速度を決定するために使用されるパイロットの静的対気速度計によって発生します。これらの測定誤差は、密度誤差、圧縮率誤差、および較正誤差です。これらの誤差を実際の対気速度に適用すると、指示対気速度が得られます。
密度エラーは、高度が高いほど空気の密度が低くなるため発生します。その結果、高高度では対気速度計の指示値が実際の対気速度よりも低くなります。高度における空気密度と海面での標準日の空気密度の差または誤差を真対気速度に適用すると、等価対気速度 (EAS) が得られます。等価対気速度は、対気速度計に影響を及ぼす大気密度の変化によって修正された実際の対気速度です。
圧縮性エラーは、空気の圧縮抵抗能力が限られているために発生します。この能力は、高度の増加、速度の増加、または音量の制限によって低下します。対気速度計内には一定量の空気が閉じ込められています。高高度および高対気速度で飛行する場合、較正対気速度 (CAS) は常に同等の対気速度よりも高くなります。校正された対気速度は、対気速度計に影響を及ぼす空気の圧縮効果を考慮して修正された等価対気速度です。
キャリブレーション エラー は、特定の航空機の設計に固有のものです。校正誤差は、対気速度計内の大気圧と等しい圧力を維持するための静的通気口の位置と配置の結果です。静的通気口の位置と配置、および航空機の迎え角と速度によって、対気速度計内の圧力が決まり、それによって対気速度計の校正誤差の量も決まります。校正表は通常、パイロット操作ハンドブック (POH) またはその他の航空機仕様書に記載されています。この校正表を使用して、校正された対気速度から対気速度計の校正誤差を修正することで、指示対気速度 (IAS) が決定されます。
以下のデータは、フラップ偏向がゼロの航空機の対気速度計の対気速度校正表です。対気速度校正テーブルは、校正誤差を除去して指示対気速度 (IAS) を校正対気速度 (CAS) に変換します。
flaps0IAS = 40:10:140; flaps0CAS = [43 51 59 68 77 87 98 108 118 129 140];
飛行からの指示対気速度 (IAS) と対気速度校正表を使用して、飛行の校正対気速度 (CAS) を決定します。
CAS = interp1( flaps0IAS, flaps0CAS, fltdata(:,4) );
大気の特性、温度 (T)、音速 (a)、圧力 (P)、密度 (rho) は、atmoscoesa 関数を使用して標準日の高度で決定されます。
[T, a, P, rho]= atmoscoesa( alt );
較正対気速度 (CAS) と大気の特性が決定されると、correctairspeed 関数を使用して真対気速度 (Vt) を計算できます。
Vt = correctairspeed( CAS, a, P, 'CAS', 'TAS' );
航空機用デジタルDATCOMデータのインポート
datcomimport 関数を使用して、デジタル DATCOM データを MATLAB に取り込みます。この空気力学情報の単位はフィートと度です。
data = datcomimport( 'astflight.out', true, 0 );これはデジタルDATCOM出力ファイルで確認でき、インポートされたデータを調べると、
と
最初のアルファ値にのみデータがあります。デフォルトでは、欠落しているデータ ポイントは 99999 に設定され、fillmissing の「前の」方法を使用して埋められます。欠落しているデータ ポイントは、最初のアルファの値で埋められます。これらのデータ ポイントはすべてのアルファ値に使用されるためです。
data{1}.cyb = fillmissing(data{1}.cyb, "previous", "MissingLocations", data{1}.cyb == 99999);
data{1}.cnb = fillmissing(data{1}.cnb, "previous", "MissingLocations", data{1}.cnb == 99999);
data{1}.clq = fillmissing(data{1}.clq, "previous", "MissingLocations", data{1}.clq == 99999);
data{1}.cmq = fillmissing(data{1}.cmq, "previous", "MissingLocations", data{1}.cmq == 99999);飛行条件における安定性と動的微分係数の補間
デジタル DATCOM 構造の安定性と動的導関数は、マッハ数、迎え角(度)、高度(フィート)の関数である 3D テーブルです。3D 線形補間 (griddedInterpolant) を実行するには、導関数テーブルのインデックスが点の単調な完全グリッドである必要があります。この形式のインデックスは、nd grid 関数によって生成されます。
[mnum, alp, h] = ndgrid( data{1}.mach, data{1}.alpha, data{1}.alt );導関数の角度単位は度であるため、迎え角 (アルファ) の単位は関数 convang によってラジアンから度に変換されます。
alphadeg = convang( alpha, 'rad', 'deg' );
飛行のマッハ数は、音速 (a) と対気速度 (Vt) を使用して関数 machnumber によって計算されます。
Mach = machnumber( convvel( [Vt zeros(size(Vt,1),2)], 'kts', 'm/s' ), a );
GriddedInterpolant を使用すると、微分表を線形補間して、飛行条件での静的および動的微分を見つけることができます。
F = griddedInterpolant( mnum, alp, h, pagetranspose(data{1}.cd), 'linear');
cd = F(Mach, alphadeg, alt);
F = griddedInterpolant( mnum, alp, h, pagetranspose(data{1}.cyb), 'linear');
cyb = F(Mach, alphadeg, alt);
F = griddedInterpolant( mnum, alp, h, pagetranspose(data{1}.cl), 'linear');
cl = F(Mach, alphadeg, alt);
F = griddedInterpolant( mnum, alp, h, pagetranspose(data{1}.cyp), 'linear');
cyp = F(Mach, alphadeg, alt);
F = griddedInterpolant( mnum, alp, h, pagetranspose(data{1}.clad), 'linear');
clad = F(Mach, alphadeg, alt);空気力学係数を計算する
飛行条件の導関数が見つかると、空力係数を計算できます。
空力係数の計算に使用される基準長さと面積は、デジタル DATCOM 構造から抽出されます。
cbar = data{1}.cbar;
Sref = data{1}.sref;
bref = data{1}.blref;導関数の角度単位は度なので、横滑り角 (ベータ) の単位は関数 convang によってラジアンから度に変換されます。
betadeg = convang( beta, 'rad', 'deg' );
空力係数を計算するには、導関数と同様に、安定軸に機体の角速度 (オメガ) を指定する必要があります。関数 dcmbody2stability は、横滑り角 (ベータ) がゼロに設定されている場合に、ボディ軸から安定軸 (Tsb) への方向余弦行列を生成します。
Tsb = dcmbody2stability( alpha );
安定軸 (omega_stab) の角速度を見つけるには、迎え角の変化率 (alpha_dot) も必要です。関数 diff は、度単位のアルファをデータ サンプル時間 (0.50 秒) で割って、迎え角の変化率 (alpha_dot) を概算するために使用されます。
alpha_dot = diff( alphadeg/0.50 );
この計算では、alpha_dot の長さを他の配列と一致させるために、alpha_dot の最後の値が保持されます。これは、diff 関数が入力より 1 つ短い配列を返すために必要です。
alpha_dot = [alpha_dot; alpha_dot(end)];
飛行データに対して、安定軸 (omega_stab) の角速度が計算されます。角速度は 3 次元行列に再構成され、ボディ軸から安定軸 (Tsb) への方向余弦行列の 3 次元行列と乗算されます。
omega_temp = reshape((omega - [zeros(size(alpha)) alpha_dot zeros(size(alpha))])',3,1,length(omega)); for k = length(omega):-1:1 omega_stab(k,:) = (Tsb(:,:,k)*omega_temp(:,:,k))'; end
抗力係数 (CD)、横力係数 (CY)、揚力係数 (CL) を計算します。convvel 関数は、対気速度 (Vt) の単位を導関数の単位と一致させるために使用されます。
CD = cd; CY = ( cyb.*betadeg ) + ((( cyp.*omega_stab(:,1) )*bref )/( 2./convvel(Vt, 'kts', 'ft/s') )); CL = cl + ((( clad.*alpha_dot )*cbar )/( 2./convvel(Vt, 'kts', 'ft/s') ));
計算力
空気力を計算するには、抗力、横力、揚力の空気力係数が使用されます。
空気力学の力を計算するには動圧が必要です。関数 dpressure は、空気速度 (Vt) と密度 (rho) から動圧を計算します。convvel 関数は、密度 (rho) の単位と一致する対気速度 (Vt) の単位を取得するために使用されます。
qbar = dpressure( convvel( [Vt zeros(size(Vt,1),2)], 'kts', 'm/s' ), rho );
ボディ軸の力を求めるには、安定軸からボディ軸への方向余弦行列 (Tbs) が必要です。安定軸からボディ軸への方向余弦行列 (Tbs) は、ボディ軸から安定軸への方向余弦行列 (Tsb) の転置です。3D 配列の転置を取るには、pagetranspose 関数を使用します。
Tbs = pagetranspose(Tsb);
飛行データ ポイントをループして、空気力が計算され、安定性からボディ軸に変換されます。convpres 関数は、参照領域 (Sref) の単位と一致する動圧 (qbar) の単位を取得するために使用されます。
for k = length(qbar):-1:1 forces_lbs(k,:) = Tbs(:,:,k)*(convpres(qbar(k),'Pa','psf')*Sref*[-CD(k); CY(k); -CL(k)]); end
ボディ軸には一定の推力が推定されます。
thrust = ones(length(forces_lbs),1)*[200 0 0];
一定推力推定値が空気力に追加され、単位がメートル法に変換されます。
forces = convforce((forces_lbs + thrust),'lbf','N');
G力を推定する
計算された力を使用して、飛行中の G 力を推定します。
加速度は計算された力と、convmass を使用してキログラムに変換された質量を使用して推定されます。加速度は convacc を使用して G 力に変換されます。
N = convacc(( forces/convmass(84.2,'slug','kg') ),'m/s^2',"G's"); N = N .* [1,1,-1];
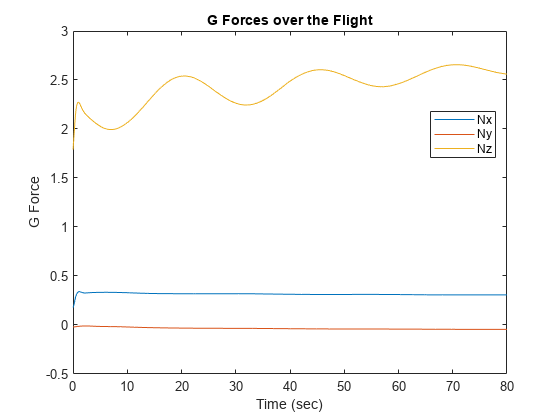
G 力は飛行中にプロットされます。
h1 = figure; plot(fltdata(:,1), N); xlabel('Time (sec)') ylabel('G Force') title('G Forces over the Flight') legend('Nx','Ny','Nz','Location','Best')
close(h1);
参考
atmoscoesa | convacc | convvel | correctairspeed | datcomimport | dpressure