このページは機械翻訳を使用して翻訳されました。最新版の英語を参照するには、ここをクリックします。
Simulink Control Design による機体のトリムと線形化
この例では、Simulink ® Control Design™ ソフトウェアを使用して機体をトリミングおよび線形化する方法を示します。
従来の設計手法で自動操縦装置を設計するには、いくつかの調整された飛行条件に対する機体のピッチダイナミクスの線形モデルが必要です。MATLAB ® テクニカル コンピューティング環境では、トリム条件を決定し、非線形 Simulink ® および Aerospace Blockset ™ モデルから直接線形状態空間モデルを導出できます。このステップにより時間が節約され、モデルの検証に役立ちます。Simulink Control Design 関数を使用すると、オープンループ周波数または時間応答の観点から機体の動きを視覚化できます。
誘導モデルの初期化
最初の問題は、昇降舵の偏差と、結果として得られる平衡化した本体比 (q) を見つけることです。これにより、ミサイルが設定速度で飛行しているときの所定の入射角値が生成されます。平衡化条件が見つかると、その平衡化条件周りの状態での摂動のダイナミクスに対する線形モデルを導出できます。
open_system('aeroblk_guidance_airframe');

状態値の定義
トリミングの状態値を定義します。
高さ [m]
マッハ数
発生率 [rad]
飛行経路角度 [rad]
総速度 [m/s]
初期ピッチボディレート [rad/sec]
heightIC = 10000/m2ft; machIC = 3; alphaIC = -10*d2r; thetaIC = 0*d2r; velocityIC = machIC*(340+(295-340)*heightIC/11000); pitchRateIC = 0;
操作点と状態仕様の設定
最初の状態仕様は位置状態です。2 番目の状態指定は Theta です。どちらも既知のものですが、定常状態にはありません。3 番目の状態の仕様は、変数 w が定常状態にあるボディ軸の角速度です。
opspec = operspec('aeroblk_guidance_airframe');
opspec.States(1).Known = [1;1];
opspec.States(1).SteadyState = [0;0];
opspec.States(2).Known = 1;
opspec.States(2).SteadyState = 0;
opspec.States(3).Known = [1 1];
opspec.States(3).SteadyState = [0 1];
操作点の検索、I/O の設定、線形化
状態仕様を満たす動作点を見つけ、指定された入力と出力を使用して線形モデルを導出します。
op = findop('aeroblk_guidance_airframe',opspec); io(1) = linio('aeroblk_guidance_airframe/Fin Deflection',1,'input'); io(2) = linio('aeroblk_guidance_airframe/Selector',1,'output'); io(3) = linio(sprintf(['aeroblk_guidance_airframe/Aerodynamics &\n', ... 'Equations of Motion']),3,'output'); sys = linearize('aeroblk_guidance_airframe',op,io);
Operating point search report:
---------------------------------
opreport =
Operating point search report for the Model aeroblk_guidance_airframe.
(Time-Varying Components Evaluated at time t=0)
Operating point specifications were successfully met.
States:
----------
Min x Max dxMin dx dxMax
__________ __________ __________ __________ __________ __________
(1.) aeroblk_guidance_airframe/Aerodynamics & Equations of Motion/3DOF (Body Axes)/Position
0 0 0 -Inf 967.6649 Inf
-3047.9999 -3047.9999 -3047.9999 -Inf -170.6254 Inf
(2.) aeroblk_guidance_airframe/Aerodynamics & Equations of Motion/3DOF (Body Axes)/Theta
0 0 0 -Inf -0.21604 Inf
(3.) aeroblk_guidance_airframe/Aerodynamics & Equations of Motion/3DOF (Body Axes)/U,w
967.6649 967.6649 967.6649 -Inf -14.0977 Inf
-170.6254 -170.6254 -170.6254 0 -7.439e-08 0
(4.) aeroblk_guidance_airframe/Aerodynamics & Equations of Motion/3DOF (Body Axes)/q
-Inf -0.21604 Inf 0 3.3582e-08 0
Inputs:
----------
Min u Max
_______ _______ _______
(1.) aeroblk_guidance_airframe/Fin Deflection
-Inf 0.13615 Inf
Outputs:
----------
Min y Max
__________ __________ __________
(1.) aeroblk_guidance_airframe/q
-Inf -0.21604 Inf
(2.) aeroblk_guidance_airframe/az
-Inf -7.439e-08 Inf
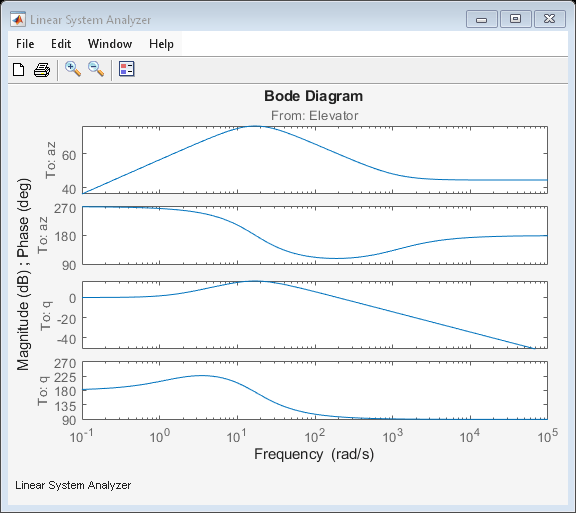
平衡化した状態の選択、LTI オブジェクトの作成、ボード応答のプロット
状態ベクトル内の目的の状態のインデックスを見つけます。次に、LTI オブジェクトを作成し、周波数応答をボード線図として表示します。
names = sys.StateName; q_idx = find(strcmp('q',names)); az_idx = find(strcmp('U,w(2)',names)); airframe = ss(sys.A([az_idx q_idx],[az_idx q_idx]),sys.B([az_idx q_idx],:),sys.C(:,[az_idx q_idx]),sys.D); set(airframe,'inputname',{'Elevator'}, ... 'outputname',[{'az'} {'q'}]); linearSystemAnalyzer('bode',airframe);
著作権 1990-2023 The MathWorks, Inc.