最小 p ノルム最適 IIR フィルターの設計
この例では、制約なし最小 P 次最適化アルゴリズムを使用する、任意の振幅応答をもつ最適 IIR フィルターの設計方法を示します。
IIRLPNORM の基本
iirlpnorm アルゴリズムは、以下のように、いくつかの側面で従来的な IIR 設計アルゴリズムとは異なります。
設計が z-領域で直接行われる。双一次変換が不要である。
分子と分母の次数が異なる可能性がある。
基本的なローパス、ハイパス、バンドパス、およびバンドストップ フィルターに加えて、任意の振幅応答をもつ IIR フィルターを設計できる。
ローパス設計
ローパスやハイパスなどの簡単な設計では、通過帯域周波数および阻止帯域周波数を指定します。遷移帯域は、アルゴリズムによって don't-care 領域と見なされます。
hiirlpnorm = designfilt("lowpassiir",FilterOrder=8,PassbandFrequency=.4,StopbandFrequency=.5, ... DesignMethod="lpnorm",SystemObject=true)
hiirlpnorm =
dsp.SOSFilter with properties:
Structure: 'Direct form II'
CoefficientSource: 'Property'
Numerator: [4×3 double]
Denominator: [4×3 double]
HasScaleValues: true
ScaleValues: [0.5146 1 1 1 1]
Show all properties
比較のために、以下の楕円フィルター設計を検証します。
hellip = designfilt("lowpassiir",FilterOrder=8,PassbandFrequency=.4,PassbandRipple=.0084,StopbandAttenuation=66.25, ... DesignMethod="ellip",SystemObject=true)
hellip =
dsp.SOSFilter with properties:
Structure: 'Direct form II'
CoefficientSource: 'Property'
Numerator: [4×3 double]
Denominator: [4×3 double]
HasScaleValues: true
ScaleValues: [0.7442 0.7330 1.4088 0.0154 1]
Show all properties
FA = filterAnalyzer(hiirlpnorm,hellip,FilterNames=["iirlpnormDesign","ellipDesign"]);

2 つのフィルターの応答は非常によく似ています。通過帯域にズームすると、その点が強調されます。ただし、iirlpnorm を使用して設計されたフィルターの振幅は、0 dB 未満となるようには制約されません。
zoom(FA,"xy",[0 .44 -.0092 .0052]);
異なる分子次数と分母次数
iirlpnorm アルゴリズムでは、楕円フィルターと非常によく似た設計を得られるだけでなく、高度な柔軟性を得られます。たとえば、分母と分子を別々に設定できます。
hiirlpnorm = designfilt("lowpassiir",NumeratorOrder=8,DenominatorOrder=6,PassbandFrequency=.4,StopbandFrequency=.5, ... DesignMethod="lpnorm",SystemObject=true)
hiirlpnorm =
dsp.SOSFilter with properties:
Structure: 'Direct form II'
CoefficientSource: 'Property'
Numerator: [4×3 double]
Denominator: [4×3 double]
HasScaleValues: true
ScaleValues: [0.6771 1 1 1 1]
Show all properties
楕円フィルター (およびその他の従来的な IIR 設計) を使用する場合、分子と分母の次数を両方変更しなければなりません。
hellip = designfilt("lowpassiir",FilterOrder=6,PassbandFrequency=.4,PassbandRipple=.0084,StopbandAttenuation=58.36, ... DesignMethod="ellip",SystemObject=true)
hellip =
dsp.SOSFilter with properties:
Structure: 'Direct form II'
CoefficientSource: 'Property'
Numerator: [3×3 double]
Denominator: [3×3 double]
HasScaleValues: true
ScaleValues: [0.7281 1.6472 0.0251 1]
Show all properties
filterAnalyzer(hiirlpnorm,hellip,FilterNames=["iirlpnormDesignDiffOrder","ellipDesignDiffOrder"]);
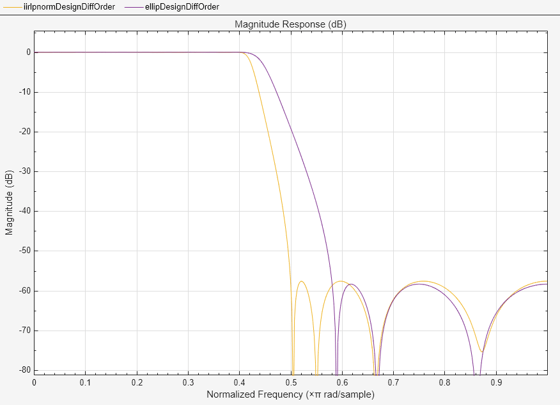
楕円設計 (緑色で表示) の遷移幅が明らかに広がったことがわかります。
設計の重み付け
等リップル設計または最小二乗設計と同様に、最適化基準に重み付けして設計を近似するように変更できます。ただし、等リップル設計と異なる点は、その高度な柔軟性のため、各周波数帯域ではなく各周波数点に対して異なる重みを付けられる点です。
以下の 2 つのハイパス フィルターを検討してください。
h1 = designfilt("highpassiir",NumeratorOrder=6,DenominatorOrder=4,StopbandFrequency=.6,PassbandFrequency=.7, ... DesignMethod="lpnorm",PassbandWeight=1,StopbandWeight=10,SystemObject=true)
h1 =
dsp.SOSFilter with properties:
Structure: 'Direct form II'
CoefficientSource: 'Property'
Numerator: [3×3 double]
Denominator: [3×3 double]
HasScaleValues: false
Show all properties
h2 = designfilt("highpassiir",NumeratorOrder=6,DenominatorOrder=4,StopbandFrequency=.6,PassbandFrequency=.7, ... DesignMethod="lpnorm",PassbandWeight=1,StopbandWeight=[100 10],SystemObject=true)
h2 =
dsp.SOSFilter with properties:
Structure: 'Direct form II'
CoefficientSource: 'Property'
Numerator: [3×3 double]
Denominator: [3×3 double]
HasScaleValues: false
Show all properties
filterAnalyzer(h1,h2,FilterNames=["SameWeightEntireBand","DifferentWeightsStopband"]);
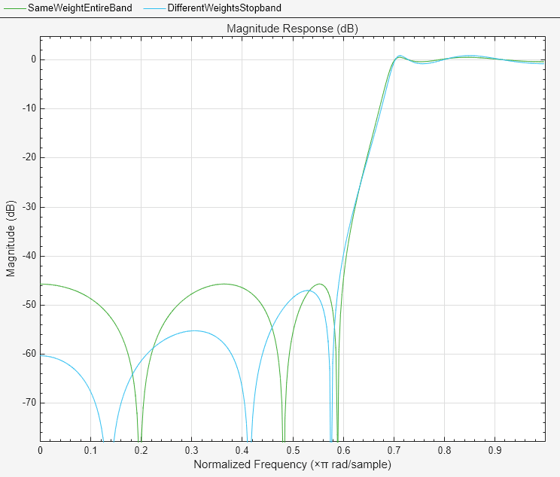
最初の設計は、帯域ごとに同じ重み (阻止帯域で 10、通過帯域で 1) を使用しています。2 番目の設計では、周波数点ごとに異なる重みが使用されています。これによって、一部のアプリケーションで必要となる傾斜阻止帯域を簡単に得られます。阻止帯域の部分での追加の減衰は、通過帯域リップルと遷移幅が大きくなることによって発生します。
p ノルム
簡潔に説明すると、最適な設計は、実際に設計されたフィルターと理想的なフィルターの間の p ノルムでの誤差を最小化することによって得られます。ノルムに異なる値がある場合、結果として異なる設計が得られます。P のノルムを指定する場合、実際には、'InitNorm' と 'Norm' という 2 つの値を指定します。'InitNorm' はアルゴリズムが使用するノルムの開始値であり、'Norm' は設計を最適化する目標値となる最終 (実際) 値です。低い開始値を使用して最適化を開始すると、アルゴリズムが収束しやすくなります。
既定の設定では、アルゴリズムは、2 ノルム的に設計の最適化を開始しますが、最終的には 128 ノルム的に最適化します。128 ノルムを使用すると、無限大ノルムの良好な近似が得られます。したがって、設計は、等リップルになる傾向があります。最小二乗設計には、ノルムを 2 に設定しなければなりません。たとえば、以下のローパス フィルターを検討してください。
pthnormFilt = designfilt("lowpassiir",NumeratorOrder=10,DenominatorOrder=7,PassbandFrequency=.25,StopbandFrequency=.35, ... DesignMethod="lpnorm",Norm=2,SystemObject=true); filterAnalyzer(pthnormFilt)
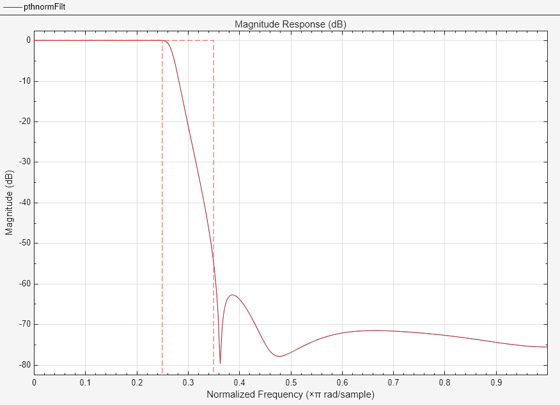
任意の整形済み振幅
iirlpnorm のもう 1 つの重要な機能は、基本的なローパス、ハイパス、バンドパス、およびバンドストップ フィルター以外のフィルターを設計できることです。詳細については、任意の振幅フィルター設計の例を参照してください。ここで、いくつかの例を示します。レイリー フェージング チャネルとルビジウム 87 原子蒸気の光吸収です。
レイリー フェージング チャネル
以下に、レイリー フェージング無線通信チャネルをシミュレーションする場合のノイズ整形のためのフィルターを示します。
F1 = 0:0.01:0.4; A1 = 1.0 ./ (1 - (F1./0.42).^2).^0.25; F2 = [0.45 1]; A2 = [0 0]; rayleighFilt = designfilt("arbmagiir",NumeratorOrder=4,DenominatorOrder=6,NumBands=2, ... BandFrequencies1=F1,BandAmplitudes1=A1, ... BandFrequencies2=F2,BandAmplitudes2=A2, ... DesignMethod="lpnorm",SystemObject=true)
rayleighFilt =
dsp.SOSFilter with properties:
Structure: 'Direct form II'
CoefficientSource: 'Property'
Numerator: [3×3 double]
Denominator: [3×3 double]
HasScaleValues: true
ScaleValues: [0.3358 1 1 1]
Show all properties
filterAnalyzer(rayleighFilt)
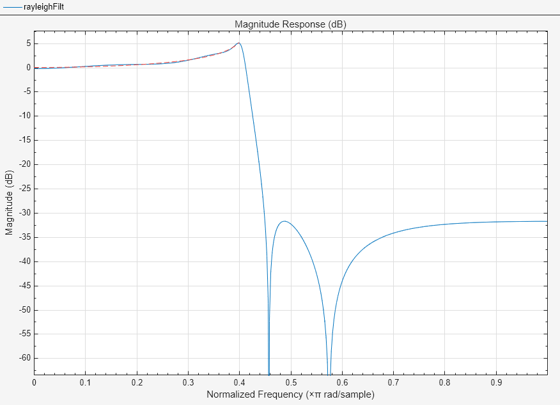
ルビジウム 87 原子蒸気の光吸収
以下の設計は、特定のガス内での光吸収のモデルを作成します。結果として得られるフィルターは、線形位相に非常に近似したフィルターとなります。
Nb = 12; Na = 10; F = linspace(0,1,100); As = ones(1,100)-F*0.2; Absorb = [ones(1,30),(1-0.6*bohmanwin(10))', ... ones(1,5), (1-0.5*bohmanwin(8))',ones(1,47)]; A = As.*Absorb; W = [ones(1,30) ones(1,10)*.2 ones(1,60)]; rubidiumFilt = designfilt("arbmagiir",NumeratorOrder=Nb,DenominatorOrder=Na, ... Frequencies=F,Amplitudes=A, ... Weights=W,Norm=2,DensityFactor=30, ... DesignMethod="lpnorm",SystemObject=true)
rubidiumFilt =
dsp.SOSFilter with properties:
Structure: 'Direct form II'
CoefficientSource: 'Property'
Numerator: [6×3 double]
Denominator: [6×3 double]
HasScaleValues: true
ScaleValues: [0.1407 1 1 1 1 1 1.6379]
Show all properties
filterAnalyzer(rubidiumFilt)
