イメージ フュージョン
このツールボックスで、イメージ フュージョンのために必要な関数は、wfusimg 1 つだけです。この関数の詳細については、リファレンス ページを参照してください。フュージョン手法の詳細については、wfusmat 関数を参照してください。
この節では、次のことを行う方法について学習します。
分解構造からのイメージのマージ
分解構造からのイメージの復元
ウェーブレットを使用したイメージ フュージョンの基本原理は、フュージョン手法を Approximation 係数と Detail 係数に適用し、元の 2 つのイメージのウェーブレット分解構造をマージすることです (参考文献 の [MisMOP03] および [Zee98] を参照)。
その 2 つのイメージは同じサイズでなければならず、共通のカラーマップをもつインデックス付きイメージに関連付けられている必要があります (イメージのリサイズについては、wextend を参照)。
2 つの例を見ていきます。1 つ目の例では、2 つの異なるイメージをマージして 1 つの新しいイメージを生成します。2 つ目の例では、あるイメージの 2 つの不鮮明なバージョンから元のイメージを復元します。
2 つのイメージの融合
この例では、2 つのイメージを融合して新しいイメージを作成する方法を示します。
能面と胸像のイメージを読み込みます。
load mask x1 = X; load bust x2 = X;
db2 ウェーブレットを使用して、レベル 5 ウェーブレット分解からの 2 つのイメージをマージします。Approximation と Detail の両方の平均値を取って融合を実行します。
wv = 'db2'; lv = 5; xfusmean = wfusimg(x1,x2,wv,lv,'mean','mean');
2 つのイメージを再度マージしますが、今度は Approximation の最大値と Detail の最小値を取って融合を実行します。
xfusmaxmin = wfusimg(x1,x2,wv,lv,'max','min');
元のイメージおよび融合したイメージをプロットします。
subplot(2,2,1) image(x1) axis square title('Mask') subplot(2,2,2) image(x2) axis square title('Bust') subplot(2,2,3) image(xfusmean) axis square title('Synthesized Image: mean-mean') subplot(2,2,4) image(xfusmaxmin) axis square title('Synthesized Image: max-min') colormap(map)

2 つの不鮮明なバージョンからのイメージの復元
この例では、元のイメージの 2 つの不鮮明なバージョンからイメージを復元する方法を示します。
1 つの元イメージの 2 つの不鮮明なバージョンを読み込みます。
load cathe_1 x1 = X; load cathe_2 x2 = X;
smy4 ウェーブレットを使用して、レベル 5 ウェーブレット分解からの 2 つのイメージをマージします。Approximation と Detail の両方の係数の絶対値の最大値を取って、融合を実行します。
wv = 'sym4'; lv = 5; xfus = wfusimg(x1,x2,wv,lv,'max','max');
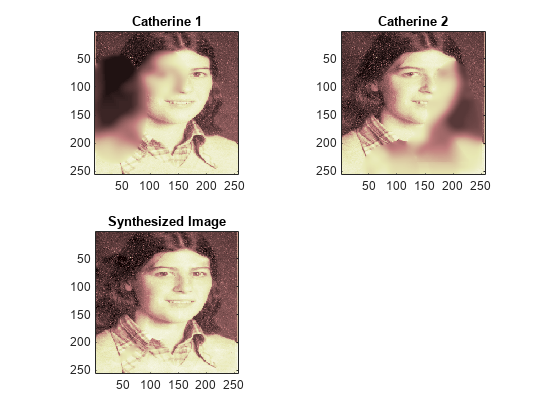
元のイメージおよび融合したイメージをプロットします。
subplot(2,2,1) image(x1) axis square title('Catherine 1') subplot(2,2,2) image(x2) axis square title('Catherine 2') subplot(2,2,3) image(xfus) axis square title('Synthesized Image') colormap(map)