bernoulli
ベルヌーイ数とベルヌーイ多項式
説明
例
偶数項と奇数項のベルヌーイ数
0 番目のベルヌーイ数は 1 です。次のベルヌーイ数は、定義に応じて -1/2 または 1/2 になります。関数 bernoulli は、-1/2 を使用します。偶数項 n > 1 のベルヌーイ数では、正の数と負の数が交互に並びます。奇数項 n > 2 のベルヌーイ数は、0 となります。
0 から 10 までの偶数項のベルヌーイ数を計算します。これらの項はシンボリック オブジェクトではないため、bernoulli は浮動小数点の結果を返します。
bernoulli(0:2:10)
ans =
1.0000 0.1667 -0.0333 0.0238 -0.0333 0.0758項をシンボリック オブジェクトに変換して同じベルヌーイ数を計算します。
bernoulli(sym(0:2:10))
ans = [ 1, 1/6, -1/30, 1/42, -1/30, 5/66]
1 から 11 までの奇数項のベルヌーイ数を計算します。
bernoulli(sym(1:2:11))
ans = [ -1/2, 0, 0, 0, 0, 0]
ベルヌーイ多項式
ベルヌーイ多項式では、2 つの入力引数で bernoulli を使用します。
ベルヌーイ多項式の変数 x、y および z について、それぞれの 1 次、2 次および 3 次導関数を計算します。
syms x y z bernoulli(1, x) bernoulli(2, y) bernoulli(3, z)
ans = x - 1/2 ans = y^2 - y + 1/6 ans = z^3 - (3*z^2)/2 + z/2
2 番目の引数が数値である場合、bernoulli はその数について多項式を評価します。ここでは、入力引数はシンボリック数ではないので結果は浮動小数点数になります。
bernoulli(2, 1/3)
ans = -0.0556
シンボリック厳密解の結果を取得するためには、少なくとも 1 つの数値をシンボリック オブジェクトに変換します。
bernoulli(2, sym(1/3))
ans = -1/18
ベルヌーイ多項式のプロット
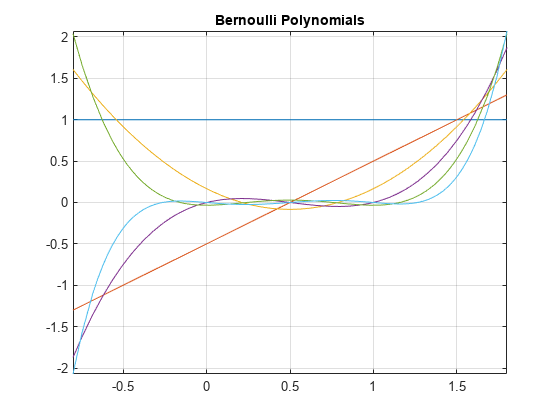
最初の 6 つのベルヌーイ多項式をプロットします。
syms x fplot(bernoulli(0:5, x), [-0.8 1.8]) title('Bernoulli Polynomials') grid on
ベルヌーイ多項式を含む式の処理
diff および expand などの多くの関数は bernoulli を含む式を処理することができます。
ベルヌーイ多項式の 1 次および 2 次導関数を求めます。
syms n x diff(bernoulli(n,x^2), x)
ans = 2*n*x*bernoulli(n - 1, x^2)
diff(bernoulli(n,x^2), x, x)
ans = 2*n*bernoulli(n - 1, x^2) +... 4*n*x^2*bernoulli(n - 2, x^2)*(n - 1)
ベルヌーイ多項式を含む式を展開します。
expand(bernoulli(n, x + 3))
ans = bernoulli(n, x) + (n*(x + 1)^n)/(x + 1) +... (n*(x + 2)^n)/(x + 2) + (n*x^n)/x
expand(bernoulli(n, 3*x))
ans = (3^n*bernoulli(n, x))/3 + (3^n*bernoulli(n, x + 1/3))/3 +... (3^n*bernoulli(n, x + 2/3))/3
入力引数
詳細
バージョン履歴
R2014a で導入