最大値、最小値、変曲点
この例では、Symbolic Math Toolbox™ を使った解析的および数値的な技法により関数の極値を求める方法を説明します。
1 次導関数:関数の局所的最小値および局所的最大値を求める
2 次導関数:関数の変曲点を求める
範囲: 上限をもつ関数
1 次導関数:局所的な最小値および最大値を求める
式の 1 次導関数を計算すると、その式の局所的な最小と最大を求めることができます。たとえば、分子と分母が多項式の有理式を作成します。
syms x
f = (3 * x^3 + 17 * x^2 + 6 * x + 1)/(2 * x^3 + x * -1 + 3)f =
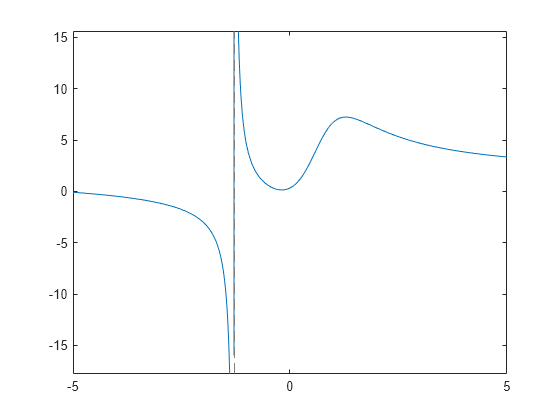
この式をプロットすると、水平方向および垂直方向の漸近線、-1 ~ 0 の間の局所的最小値、1 ~ 2 の間の局所的最大値があることが示されます。
fplot(f)
既定の設定では、この式を操作すると、結果に実数と虚数が含まれる可能性があります。実数部のみを対象とする場合は、x が一連の実数に属するという恒久的な仮定を設定できます。これにより、解に複素数が含まれなくなり、パフォーマンスも向上します。
assume(x, 'real')水平方向の漸近線を求めるには、正および負の無限大に近づく x について の極限を計算します。水平方向の漸近線は です。
[limit(f, x, sym(inf)), limit(f, x, -sym(inf))]
ans =
の垂直方向の漸近線を求めるには、 の分母を表す多項式の根を求めます。
solve(2 * x^3 + x * -1 + 3 == sym(0), x)
ans =
このような方程式の陽的な解を得るには、ソルバーをオプション MaxDegree と共に呼び出してください。このオプションでは、ソルバーで陽的な解が返されるように、多項式の最大次数が指定されます。既定では、MaxDegree = 2 です。この値を増やすと、より高階数の多項式の陽的な解を得ることができます。たとえば、MaxDegree = 3 と指定すると、陽的な解が得られます。
solve(2 * x^3 + x * -1 + 3 == 0, x, 'MaxDegree', 3)ans =
関数 vpa を使用すると、厳密解を数値的に近似できます。
vpa(ans,6)
ans =
ここで、式 f の局所的最小値と局所的最大値を求めます。点が極値 (最小または最大) である場合、その点における式の 1 次導関数はゼロになります。式の微分を計算するには、関数 diff を使用します。
g = diff(f, x)
g =
f の局所的極値を求めるには、方程式 g = 0 を解きます。MaxDegree オプションを使用する場合、ソルバーは長い陽的な解を返します。これは関数 vpa を使って近似できます。
solve(g == 0, x, 'MaxDegree', 4);
extrema = vpa(ans, 6)extrema =
式 f のプロットは、式の局所的最小値が x = -0.189、局所的最大値が x = 1.286 であることを示しています。
fplot(f) hold on plot(extrema, subs(f,extrema), '*') hold off

2 次導関数:変曲点を求める
2 次導関数を計算すると、式の変曲点を求めることができます。
h(x) = simplify(diff(f, x, 2))
h(x) =
の変曲点を求めるには、方程式 h = 0 の解を求めます。この方程式では、MaxDegree オプションを使用しても、シンボリック ソルバーは複雑な結果を返します。
solve(h == 0, x, 'MaxDegree', 4)ans =
より単純な数値結果を得るために、vpasolve を使用して方程式を数値的に解き、返される結果が式のすべての実数解に限定されるように検索範囲を指定します。
inflection = vpasolve(h == 0, x, [-inf, inf])
inflection =
式 f の変曲点は x = 0.579 と x = 1.865 の 2 つです。
fplot(f) hold on plot(extrema, subs(f,extrema), '*') plot(inflection, subs(f,inflection), '*') hold off

上限
解析的に処理できない関数もあります。関数
は、原点では非常にフラットで、多くの場合、 の付近で無限に振動し、0 に近づくと線形になり、 の付近で再び振動します。
f = @(x) tan(sin(x))-sin(tan(x))
f = function_handle with value:
@(x)tan(sin(x))-sin(tan(x))
fplot(f, [-pi , pi])
fplot で y 軸上の極限が以下のように示されたことは、ここでの目的にとって非常に重要です。
ylim
ans = 1×2
-2.5573 2.5572
で起きている現象とは
MATLAB® では倍精度の演算を使用するため、 の結果は一種の振動になります。
pi/2
ans = 1.5708
f(pi/2)
ans = 2.5161
厳密な演算を使用する Symbolic Math Toolbox は、この関数が不定であることを示します。
syms x
sym(pi/2)ans =
F = sym(f)
F =
subs(F,x,sym(pi/2))
ans =
テイラー級数
テイラー級数で値を調べることもできます。
T = taylor(F,x,'Order',10,'ExpansionPoint',0)
T =
vpa(subs(T,x,pi/2))
ans =
hold on fplot(T) ylim ([-3 3]) hold off
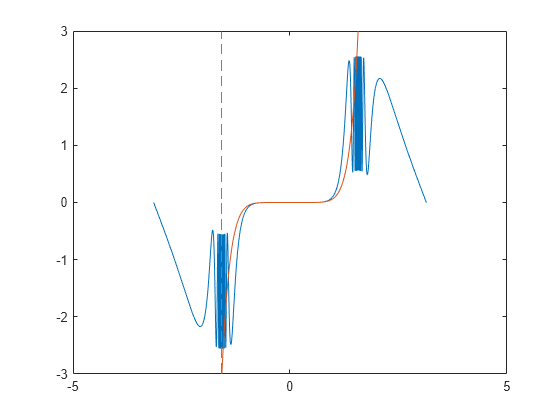
微積分
微積分により、導関数の零点で最大値になることは知られています。ただし、この関数は の近傍では微分することはできません。Symbolic Math Toolbox を使用すると、 を解析的に微分することができます。
diff(F)
ans =
fplot(diff(F), [-pi , pi])

サンプリング
の近くで関数を N 回サンプリングすると、最大値の数値近似が得られます。これで十分でしょうか。
N = 100; xValues = 3*pi/8 + pi/4*rand(1,N)
xValues = 1×100
1.8180 1.8895 1.2778 1.8955 1.6748 1.2547 1.3968 1.6076 1.9301 1.9359 1.3019 1.9404 1.9299 1.5593 1.8066 1.2895 1.5093 1.8973 1.8003 1.9317 1.6931 1.2061 1.8450 1.9117 1.7112 1.7732 1.7618 1.4862 1.6929 1.3125 1.7326 1.2031 1.3956 1.2144 1.2544 1.8248 1.7238 1.4271 1.9244 1.2052 1.5227 1.4778 1.7793 1.8026 1.3249 1.5628 1.5281 1.6857 1.7352 1.7708
ySoln = f(xValues)
ySoln = 1×100
0.7260 1.5080 1.5932 1.5614 1.3796 1.3158 2.0658 2.4586 1.8194 1.8541 1.9088 1.8793 1.8178 2.3439 0.6145 1.7447 2.0697 1.5775 0.5629 1.8290 2.4930 0.8543 1.0347 1.6931 2.2371 0.5024 0.6011 2.2489 2.4891 2.0499 1.3564 0.8308 2.0986 0.9208 1.3122 0.8011 1.7177 0.9333 1.7830 0.8466 0.6138 2.5047 0.4857 0.5809 2.2051 2.5133 2.5387 2.2247 1.2583 0.5153
max(ySoln)
ans = 2.5387
証明
数学的証明から最大値を決定します。
したがって、 と は結果として以下を意味します。
になると、 は振動し、ブローアップします。したがって、上で示したように は、この点では事実上まったく定義されません。
ここで、数値を確認することができます。
format long
1 + tan(1) ans = 2.557407724654902