fibonacci

フィボナッチ数

ページ内をすべて折りたたむ

構文

fibonacci(n)

説明

例

fibonacci(n) は n^thフィボナッチ数を返します。

例

フィボナッチ数を求める

fibonacci を使用して 6 番目のフィボナッチ数を求めます。

fibonacci(6)

ans =
     8

フィボナッチ数の最初の 10 個を求めます。

n = 1:10;
fibonacci(n)

ans =
     1     1     2     3     5     8    13    21    34    55

フィボナッチ数列で黄金比を近似する

隣接するフィボナッチ数の比は黄金比 $1.61803 . . .$ に収束します。最初の 10 個のフィボナッチ数について、この比を黄金比に対しプロットすることで収束の様子を示します。

n = 2:10;
ratio = fibonacci(n)./fibonacci(n-1);

plot(n,ratio,'--o')
hold on

line(xlim,[1.618 1.618])
hold off

Figure contains an axes object. The axes object contains 2 objects of type line.

フィボナッチ数をシンボリックに表現する

フィボナッチ数をシンボリックな入力により表現することで、シンボリック演算の中で使用します。fibonacci が入力を返します。

n 番目のフィボナッチ数を表現します。

syms n
fibonacci(n)

ans =
fibonacci(n)

大きなフィボナッチ数を求める

sym により入力をシンボリックに指定することで、大きなフィボナッチ数を求めます。シンボリックな入力は、double 型の出力の代わりにシンボリック厳密解の出力を返します。関数 double を使用してシンボリック数を double 型に変換します。

300 番目のフィボナッチ数を求めます。

num = sym(300);
fib300 = fibonacci(num)

fib300 =
222232244629420445529739893461909967206666939096499764990979600

fib300 を double に変換します。結果は浮動小数点数近似です。

double(fib300)

ans =
   2.2223e+62

シンボリック演算および倍精度演算の詳細は、数値演算またはシンボリック演算の選択を参照してください。

フィボナッチ数を用いたゴールデンスパイラル

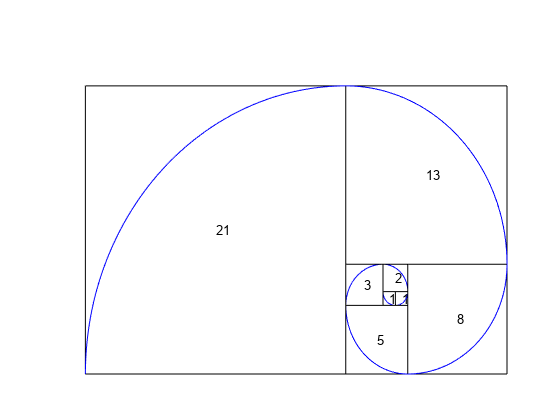
フィボナッチ数は一般的に、フィボナッチスパイラルをプロットすることで可視化されます。フィボナッチスパイラルはゴールデンスパイラルを近似します。

最初の 8 つのフィボナッチ数を用いてゴールデンスパイラルを近似します。switch ステートメントを使用して、プロット内の右、上、左、下の正方形それぞれに対応する 4 つの場合分けを定義します。eqnArc の各正方形を通過する弧の方程式を定義して、スパイラルを形にします。rectangle と fimplicit をそれぞれ使用して、正方形と弧を描画します。

x = 0;
y = 1;
syms v u

axis off
hold on

for n = 1:8

    a = fibonacci(n);

    % Define squares and arcs
    switch mod(n,4)
        case 0
            y = y - fibonacci(n-2);
            x = x - a;
            eqnArc = (u-(x+a))^2 + (v-y)^2 == a^2;
        case 1
            y = y - a;
            eqnArc = (u-(x+a))^2 + (v-(y+a))^2 == a^2;
        case 2
            x = x + fibonacci(n-1);
            eqnArc = (u-x)^2 + (v-(y+a))^2 == a^2;
        case 3
            x = x - fibonacci(n-2);
            y = y + fibonacci(n-1);
            eqnArc = (u-x)^2 + (v-y)^2 == a^2;
    end

    % Draw square
    pos = [x y a a];
    rectangle('Position', pos)

    % Add Fibonacci number
    xText = (x+x+a)/2;
    yText = (y+y+a)/2;
    text(xText, yText, num2str(a))

    % Draw arc
    interval = [x x+a y y+a];
    fimplicit(eqnArc, interval, 'b')

end