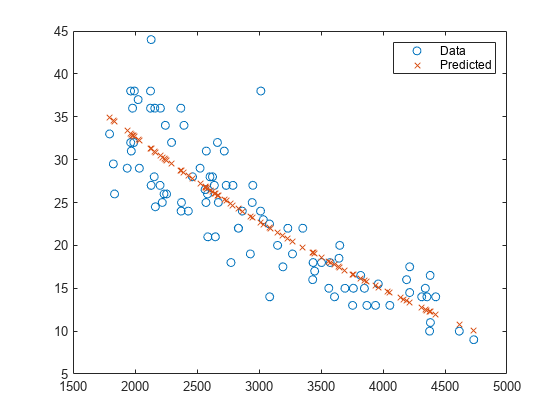
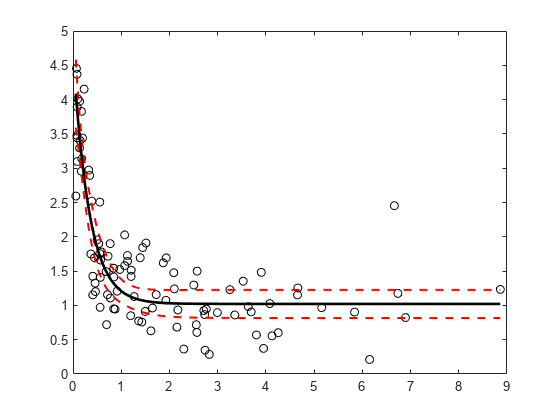
predict

クラス: NonLinearModel

非線形回帰モデルの応答予測

このページをすべて展開する

構文

ypred = predict(mdl,Xnew) [ypred,yci] = predict(mdl,Xnew) [ypred,yci] = predict(mdl,Xnew,Name,Value)

説明

ypred = predict(mdl,Xnew) は mdl 非線形回帰モデルの予測応答を Xnew 内の点に返します。

[ypred,yci] = predict(mdl,Xnew) は、真の平均応答の信頼区間を返します。

[ypred,yci] = predict(mdl,Xnew,Name,Value) では、1 つまたは複数の Name,Value の引数ペアで指定された追加オプションを使用して、応答を予測します。

入力引数

mdl

fitnlm で構築される非線形回帰モデル。

Xnew

mdl が応答を予測する点。

Xnew がテーブルまたはデータセット配列の場合、mdl に予測子名が含まれていなければなりません。
Xnew が数値行列の場合、mdl の作成に使用されたのと同じ数の変数 (列) をもたなければなりません。さらに、mdl の作成に使用された変数は、すべて数値でなければなりません。

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで Name は引数名、Value は対応する値です。名前と値の引数は他の引数の後ろにする必要がありますが、ペアの順序は関係ありません。

R2021a より前では、名前と値をそれぞれコンマを使って区切り、Name を引用符で囲みます。

`Alpha`	`0` から `1` までの正のスカラー値。`yci` の信頼度は 100(1 – `alpha`)% です。既定値: `0.05`、つまり 95% 信頼区間を意味します。
`Prediction`	予測のタイプ `'curve'` — `predict` は、近似された平均値の信頼限界を予測します。 `'observation'` — `predict` は、新しい観測値の信頼限界を予測します。この場合、新しい観測値の誤差が推定平均値の誤差と等しいことに加え、真の平均からの観測値のばらつきのため、限界値の範囲は広くなります。詳細については、`polyconf` を参照してください。既定値: `'curve'`
`Simultaneous`	信頼限界がすべての予測値を同時に対象としているか (`true`) または個別の予測子を保持しているか (`false`) を指定する論理値。1 つの予測値における曲線が範囲内であればよいのではなく、曲線全体が範囲内であることが厳密に要求されるため、同時の限界は個別の限界より広くなります。詳細については、`polyconf` を参照してください。既定値: `false`
`Weights`	正の実数値の重みのベクトルまたは関数ハンドル。ベクトルを指定する場合、`Xnew` にある観測値 (行) の数と同じ数の要素を指定しなければなりません。関数ハンドルを指定する場合、関数は予測される応答値のベクトルを入力として受け入れ、正の実数重みのベクトルを出力として返さなければなりません。重み `W` に対して `predict` は観測 `i` における誤差分散を `MSE(1/W(i))` により推定します。MSE は平均二乗誤差です。既定値:* 重み付けなし

出力引数

`ypred`	`Xnew` で予測された平均値。`ypred` は `Xnew` の各コンポーネントと同じサイズです。
`yci`	信頼区間、各行が 1 つの区間を指定する 2 列の行列。信頼区間の意味は、名前と値のペアの設定によって異なります。

例

すべて展開する

応答予測

ライブスクリプトを開く

自動車の燃費の非線形モデルを重量の関数として作成し、応答を予測します。

carsmall データから、重量の関数として自動車の燃費の指数モデルを作成します。すべての変数がほぼ同じサイズになるように、1000 のファクタで重み付けをスケーリングします。

load carsmall
X = Weight;
y = MPG;
modelfun = 'y ~ b1 + b2*exp(-b3*x/1000)';
beta0 = [1 1 1];
mdl = fitnlm(X,y,modelfun,beta0);

データに対する予測された応答を作成します。

Xnew = X;
ypred = predict(mdl,Xnew);

元の応答と予測された応答をプロットして、相違点を確認します。

plot(X,y,'o',X,ypred,'x')
legend('Data','Predicted')

Figure contains an axes object. The axes object contains 2 objects of type line. These objects represent Data, Predicted.

予測の信頼区間

ライブスクリプトを開く

自動車の燃費の非線形モデルを重量の関数として作成し、いくつかの応答の信頼区間を調べます。

load carsmall
X = Weight;
y = MPG;
modelfun = 'y ~ b1 + b2*exp(-b3*x/1000)';
beta0 = [1 1 1];
mdl = fitnlm(X,y,modelfun,beta0);

最小、平均および最大のデータ点の予測応答を作成します。

Xnew = [min(X);mean(X);max(X)];
[ypred,yci] = predict(mdl,Xnew)

ypred = 3×1

   34.9469
   22.6868
   10.0617

yci = 3×2

   32.5212   37.3726
   21.4061   23.9674
    7.0148   13.1086

ロバスト近似曲線の同時信頼区間

ライブスクリプトを開く

次の非線形回帰モデルから標本データを生成します。

$y = b_{1} + b_{2} \exp (- b_{3} x) + ϵ$

ここで、 $b_{1}$ 、 $b_{2}$ および $b_{3}$ は係数です。誤差項 $ϵ$ は平均 0 および標準偏差 0.5 の正規分布に従います。

modelfun = @(b,x)(b(1)+b(2)*exp(-b(3)*x));

rng('default') % For reproducibility
b = [1;3;2];
x = exprnd(2,100,1);
y = modelfun(b,x) + normrnd(0,0.5,100,1);

ロバスト近似オプションを使用して非線形モデルを近似します。

opts = statset('nlinfit');
opts.RobustWgtFun = 'bisquare';
b0 = [2;2;2];
mdl = fitnlm(x,y,modelfun,b0,'Options',opts);

近似した回帰モデルと 95% の同時信頼限界をプロットします。

xrange = [min(x):.01:max(x)]';
[ypred,yci] = predict(mdl,xrange,'Simultaneous',true);

figure()
plot(x,y,'ko') % observed data
hold on
plot(xrange,ypred,'k','LineWidth',2)
plot(xrange,yci','r--','LineWidth',1.5)

Figure contains an axes object. The axes object contains 4 objects of type line.

観測の重みを使用した信頼区間

ライブスクリプトを開く

標本データを読み込みます。

S = load('reaction');
X = S.reactants;
y = S.rate;
beta0 = S.beta;

観測の重みの関数ハンドルを指定した後、指定した観測の重み関数を使用してレートデータに Hougen-Watson モデルを近似します。

a = 1; b = 1;
weights = @(yhat) 1./((a + b*abs(yhat)).^2);
mdl = fitnlm(X,y,@hougen,beta0,'Weights',weights);

観測値の重みの関数を使用して、反応物レベル [100,100,100] で新しい観測値について 95% の予測区間を計算します。

[ypred,yci] = predict(mdl,[100,100,100],'Prediction','observation', ...
    'Weights',weights)

ypred = 1.8149

yci = 1×2

    1.5264    2.1033

ヒント

ノイズが追加された予測では、random を使用します。
テーブルまたはデータセット配列から作成されたモデルで使いやすい構文にするには、feval を試みてください。

参照

[1] Lane, T. P. and W. H. DuMouchel. “Simultaneous Confidence Intervals in Multiple Regression.” The American Statistician. Vol. 48, No. 4, 1994, pp. 315–321.

[2] Seber, G. A. F., and C. J. Wild. Nonlinear Regression. Hoboken, NJ: Wiley-Interscience, 2003.