スーパーコンデンサのパラメーターの特定

ライブスクリプトを開く

この例では、スーパーコンデンサのパラメーターの特定方法を説明します。実際のスーパーコンデンサから電圧と電流の波形を収集する代わりに、この例では、既知のパラメーター値を使用してスーパーコンデンサのシミュレーションを実行することによって、電圧と電流の波形を生成します。その後、例においてパラメーター特定の方法論 [1] を波形に適用します。

方法論の正確性を評価するため、この例では、特定されたパラメーターを既知のパラメーター値と比較します。この例ではまた、Simulink® Design Optimization™ ツールボックスのパラメーター推定アプリを使用して、パラメーター値の精度をさらに高める方法も説明します。

実際のスーパーコンデンサのパラメーターを経験的に特定するには、次が可能です。

電圧と電流の波形をスーパーコンデンサから収集します。
波形データと [1] の方法論を使用してパラメーター値を特定します。

モデル化されたスーパーコンデンサのパラメーターを特定するために、この例は

スーパーコンデンサのパラメーターの既知の値を使用し、モデルをシミュレートすることによって、電圧と電流の波形を生成します。
生成された波形データと [1] の方法論を使用して、スーパーコンデンサのパラメーター値を特定します。
特定されたスーパーコンデンサのパラメーター値を使用してスーパーコンデンサを設定し、シミュレーションを実行します。

このアプローチが実際のスーパーコンデンサでどのように機能するかを確認するには、以下を比較して、特定のための方法論の正確性を評価します。

既知のパラメーター値を使用して生成したデータと、特定されたパラメーター値を使用して生成したデータ。
既知のパラメーター値と特定されたパラメーター値。

正確性が十分でない場合には、Simulink Design Optimization のパラメーター推定アプリを使用して改善します。特定されたパラメーター値を最適化の開始値として使用してください。

データの生成

スーパーコンデンサの固定抵抗パラメーター、固定静電容量パラメーター、電圧依存コンデンサゲインパラメーターの既知の値を使用してモデルを設定し、シミュレートすることによって、電圧と電流の波形を生成します。入力電流をモデル化し、現実的な値を使用してスーパーコンデンサの物理特性と自己放電抵抗を構成します。

modelName = 'SupercapacitorFromData';
open_system(modelName);

既知のパラメーター値を使用してスーパーコンデンサを設定します。

SupercapacitorFromDataParameterConfiguration;

次の異なる 3 つのフェーズにおけるスーパーコンデンサの動作を観察します。

定電流による充電
即時分岐から遅延分岐への電荷再分配
即時分岐および遅延分岐から長期分岐への電荷再分配

sim(modelName)

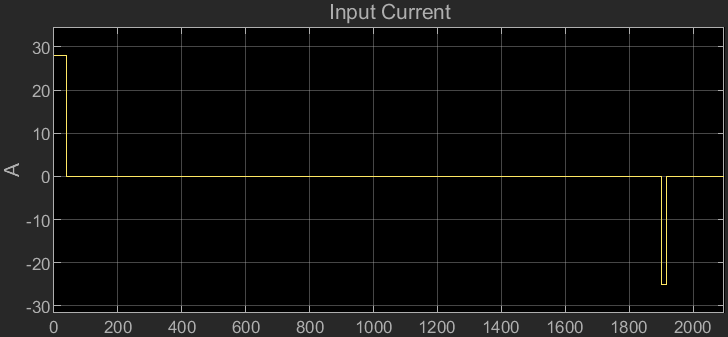
パラメーターの特定の実行

シミュレーションからの波形データを使用し、[1] で説明されている方法論を適用します。

即時分岐パラメーターの特定

特定を行う最初の段階で、完全に放電済みのスーパーコンデンサが定電流で充電されます。この方法では、即時分岐の時定数が比較的小さいため、すべての初期電荷が即時分岐に蓄積されると仮定します。

即時分岐パラメーターを計算するには、電荷特性を測定します。充電電流が $t_{1} = 20 e^{- 3} s$ で定常状態に達したら、 $v_{1}$ を測定し、次の方程式を使用して即時分岐の固定抵抗を計算します。

$R_{i} = \frac{v_{1}}{i_{1}}$

ここで、

$t_{1}$ はパラメーター特定イベント $n = 1$ の時間 (秒)。
$v_{1}$ は $t_{1}$ での端子電圧 (ボルト)。
$i_{1}$ は $t_{1}$ での充電電流 (アンペア)。
$R_{i}$ は即時分岐の固定抵抗 (オーム)。

電圧が $v_{1}$ から約 $50 e^{- 3} V$ 上昇したら、 $t_{2}$ と $v_{2}$ を測定し、次の方程式を使用して即時分岐の固定静電容量を計算します。

$C_{i 0} = i_{1} \frac{t_{2} - t_{1}}{v_{2} - v_{1}}$

ここで、

$t_{2}$ はパラメーター特定イベント $n = 2$ の時間 (秒)。
$v_{2}$ は $t_{2}$ での端子電圧 (ボルト)。
$C_{i 0}$ は即時分岐の固定静電容量 (ファラド)。

電圧が定格電圧に達したら、 $v_{3}$ と $t_{3}$ を測定し、充電電流をオフにします。 $20 e^{- 3} s$ 後、充電電流が定常値 $0 A$ に達したら、 $t_{4}$ と $v_{4}$ を測定し、次の方程式を使用して電圧依存の静電容量係数を計算します。

$t_{4} = t_{3} + 20 e^{- 3}$

$C_{i 1} = \frac{2}{v_{4}} (\frac{i_{1} (t_{4} - t_{1})}{v_{4}} - C_{i 0})$

ここで、

$t_{3}$ はパラメーター特定イベント $n = 3$ の時間 (秒)。
$v_{3}$ は $t_{3}$ での端子電圧 (ボルト)。
$t_{4}$ はパラメーター特定イベント $n = 4$ の時間 (秒)。
$v_{4}$ は $t_{4}$ での端子電圧 (ボルト)。
$C_{i 1}$ は電圧依存の静電容量係数 (電圧あたりのファラド)。

これらの計算を実行するには、次のスクリプトを実行します。

SupercapacitorFromDataParameterImmediateIdentification;

遅延分岐パラメーターの特定

第 2 段階の特定で、電荷は即時分岐から遅延分岐に再分配されます。

遅延分岐パラメーターを計算するには、電荷保持特性を測定します。

電圧が $v_{4}$ から約 $50 e^{- 3} V$ 低下したら、 $t_{5}$ と $v_{5}$ を測定し、次の方程式を使用して遅延分岐の抵抗を計算します。

$Δ v = v_{4} - v_{5}$

$V_{c i} = v_{4} - \frac{Δ V}{2}$

$C_{d i f f} = C_{i 0} + C_{i 1} V_{c i}$

$R_{d} = \frac{(v_{4} - \frac{Δ V}{2}) (t_{5} - t_{4})}{C_{d i f f} Δ V}$

ここで、

$t_{5}$ はパラメーター特定イベント $n = 5$ の時間 (秒)。
$v_{5}$ は $t_{5}$ での端子電圧 (ボルト)。
$V_{c i}$ は合計即時静電容量が計算される際の電圧 (ボルト)。
$C_{d i f f}$ は $V_{c i}$ での合計即時静電容量 (ファラド)。
$R_{d}$ は遅延分岐の抵抗 (オーム)。

300 秒間待機してから $t_{6}$ と $v_{6}$ を測定し、次の方程式を使用して遅延分岐の静電容量を計算します。

$Q_{t o t a l} = i_{1} (t_{4} - t_{1})$

$C_{d} = \frac{Q_{t o t a l}}{v_{6}} - (C_{i 0} + \frac{C_{i 1}}{2} v_{6})$

ここで、

$t_{6}$ はパラメーター特定イベント $n = 6$ の時間 (秒)。
$v_{6}$ は $t_{6}$ での端子電圧 (ボルト)。
$Q_{t o t a l}$ はスーパーコンデンサに供給された合計電荷 (クーロン)。
$C_{d}$ は遅延分岐の静電容量 (ファラド)。

これらの計算を実行するには、次のスクリプトを実行します。

SupercapacitorFromDataParameterDelayedIdentification;

長期分岐パラメーターの特定

第 3 (最終) 段階の特定で、電荷は即時分岐と遅延分岐から長期分岐に再分配されます。

長期分岐パラメーターを計算するには、電荷保持特性を測定します。

電圧が $v_{6}$ から約 $50 e^{- 3} V$ 低下したら、 $t_{7}$ と $v_{7}$ を測定し、次の方程式を使用して長期分岐の抵抗を計算します。

$Δ v = v_{6} - v_{7}$

$R_{l} = \frac{(v_{6} - \frac{Δ V}{2}) (t 7 - t_{6})}{C_{d i f f} Δ V}$

ここで、

$t_{7}$ はパラメーター特定イベント $n = 7$ の時間 (秒)。
$v_{7}$ は $t_{7}$ での端子電圧 (ボルト)。
$R_{l}$ は長期分岐の抵抗 (オーム)。

充放電処理の開始から 30 分後に $t_{8}$ と $v_{8}$ を測定し、次の方程式を使用して長期分岐の静電容量を計算します。

$C_{l} = \frac{Q_{t o t a l}}{v_{8}} - (C_{i 0} + \frac{C_{i 1}}{2} v_{8}) - C_{d}$

ここで、

$t_{8}$ はパラメーター特定イベント $n = 8$ の時間 (秒)。
$v_{8}$ は $t_{8}$ での端子電圧 (ボルト)。
$C_{l}$ は長期分岐の静電容量 (ファラド)。

これらの計算を実行するには、次のスクリプトを実行します。

SupercapacitorFromDataParameterLongTermIdentification;

時間と電圧のデータの照合

各パラメーター特定イベントの時間と電圧のデータを MATLAB® の table で照合します。

DataTable = table((1:8)',...
    [t1 t2 t3 t4 t5 t6 t7 t8]',...
    [v1 v2 v3 v4 v5 v6 v7 v8]',...
    'VariableNames',{'Event','Time','Voltage'})

DataTable=8×3 table
    Event     Time      Voltage 
    _____    _______    ________

      1         0.02    0.071799
      2      0.51803      0.1218
      3           40      2.2717
      4        40.02      2.2019
      5       56.675      2.1519
      6       356.67      1.8473
      7       499.28      1.7973
      8         1800      1.5865

SupercapacitorFromDataPlotVoltage;

Figure contains an axes object. The axes object with title Identified and Known Supercapacitor Voltages, xlabel Time [s], ylabel Voltage [V] contains 10 objects of type line, text. One or more of the lines displays its values using only markers These objects represent Known parameters simulation, Measurements for parameter identification.

特定されたパラメーターの精度の評価

特定されたスーパーコンデンサのパラメーターを使用してモデルを設定し、シミュレートします。次に、特定されたパラメーター値の精度を評価するために、波形出力を、既知のパラメーターを使用したシミュレーションを実行して生成したデータと比較します。

SupercapacitorFromDataParameterSimulateIdentifiedParameters;

Figure contains an axes object. The axes object with title Identified and Known Supercapacitor Voltages, xlabel Time [s], ylabel Voltage [V] contains 3 objects of type line. One or more of the lines displays its values using only markers These objects represent Known parameters simulation, Measurements for parameter identification, Identified parameters simulation.

パラメーター推定アプリを使用したパラメーターの最適化

スーパーコンデンサのパラメーターの最適化を実行するには、Simulink Design Optimization ツールボックスがインストールされている必要があります。

トレースの類似性が要件に満たない場合には、特定されたパラメーター値を、Simulink Design Optimization のパラメーター推定アプリで初期パラメーター値として使用できます。

スーパーコンデンサのパラメーターを最適化するには、MATLAB コマンドウィンドウで次のように入力します。

spetool('SupercapacitorSDOParameterEstimatorSession');

最適化の結果の表示

残差平方和のコスト関数と非線形最小二乗の最適化手法を使用して作成されたパラメーターの軌跡を表示します。

openfig('SupercapacitorSDOParameterEstimatorResults');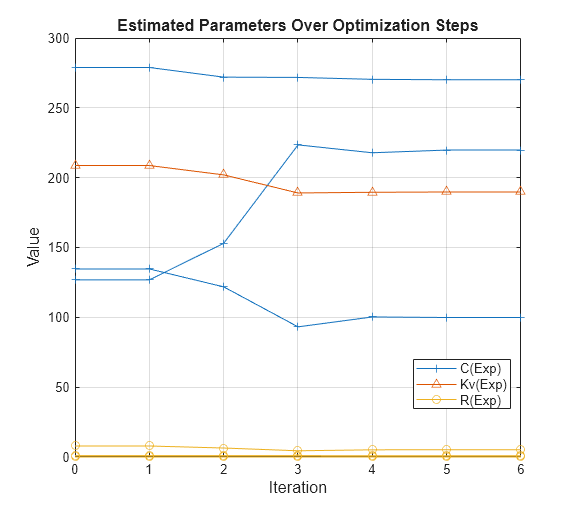

Figure contains an axes object. The axes object with title Estimated Parameters Over Optimization Steps, xlabel Iteration, ylabel Value contains 3 objects of type line. These objects represent C(Exp), Kv(Exp), R(Exp).

リアルタイムシミュレーションの結果

このモデルは、Intel® 3.5 GHz i7 マルチコア CPU を搭載した Speedgoat Performance リアルタイムターゲットマシンでテストされました。このモデルは、50 マイクロ秒のステップサイズでリアルタイム実行できます。

参考文献

[1] Zubieta, L. and R. Bonert. "Characterization of Double-Layer Capacitors for Power Electronics Applications." IEEE Transactions on Industry Applications, Vol. 36, No. 1, 2000, pp. 199-205.

スーパーコンデンサのパラメーターの特定

データの生成

パラメーターの特定の実行

即時分岐パラメーターの特定

遅延分岐パラメーターの特定

長期分岐パラメーターの特定

時間と電圧のデータの照合

特定されたパラメーターの精度の評価

パラメーター推定アプリを使用したパラメーターの最適化

最適化の結果の表示

リアルタイム シミュレーションの結果

参考文献

リアルタイムシミュレーションの結果