Clarke to Park Angle Transform
αβ0 から dq0 への変換を実装
ライブラリ:
Simscape /
Electrical /
Control /
Mathematical Transforms
説明
Clarke to Park Angle Transform ブロックは、静止基準座標系の alpha、beta、ゼロの成分を回転基準座標系の直軸、横軸、ゼロの成分に変換します。
このブロックは次の入力を受け入れます。
静止基準座標系における α-β 軸成分または多重化された成分 αβ0。[入力の数] パラメーターを使用して、2 つの入力または 3 つの入力を使用します。
変換の対応する角度の正弦値と余弦値。
平衡三相システムの場合、ゼロ成分はゼロに等しくなります。
このブロックでは、三相システムの a 相の軸を時間 t = 0 において回転基準座標系の q 軸または d 軸のいずれかに揃えるように構成できます。次の図は、三相システム、静止 αβ0 基準座標系、および回転 dq0 基準座標系における固定子巻線の磁気軸の向きを示しています。
a 軸と q 軸が最初に揃っています。
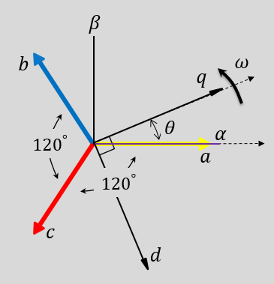
a 軸と d 軸が最初に揃っています。

どちらの場合も、角度は θ = ωt です。
θ は、q 軸に揃える場合は a 軸と q 軸の間の角度、d 軸に揃える場合は a 軸と d 軸の間の角度です。
ω は、d-q 基準座標系の回転速度です。
t は、最初の配置からの時間 (秒数) です。
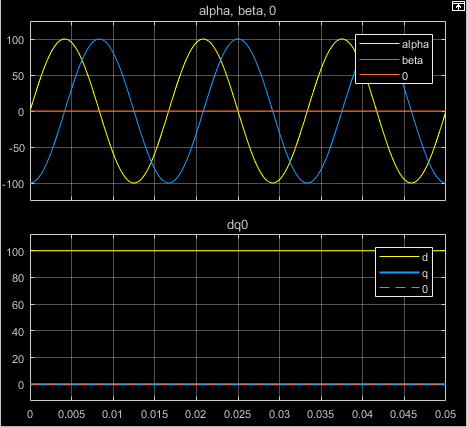
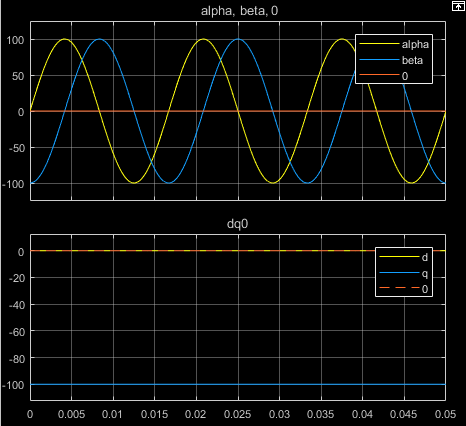
次の図は、同等の平衡な αβ0 と dq0 の各成分の時間応答を示しています。
a 相のベクトルを q 軸に揃える
a 相のベクトルを d 軸に揃える
方程式
Clarke to Park Angle Transform ブロックは、a 相を q 軸に揃える変換を次のように実装します。
ここで、
α と β は、静止基準座標系における二相システムの alpha 軸成分と beta 軸成分です。
0 は、ゼロ成分です。
d と q は、回転基準座標系における 2 軸システムの直軸成分と横軸成分です。
a 相を d 軸に揃える場合、ブロックは次の方程式を使用して変換を実装します。
端子
入力
出力
パラメーター
参照
[1] Krause, P., O. Wasynczuk, S. D. Sudhoff, and S. Pekarek. Analysis of Electric Machinery and Drive Systems. Piscatawy, NJ: Wiley-IEEE Press, 2013.