このページは前リリースの情報です。該当の英語のページはこのリリースで削除されています。

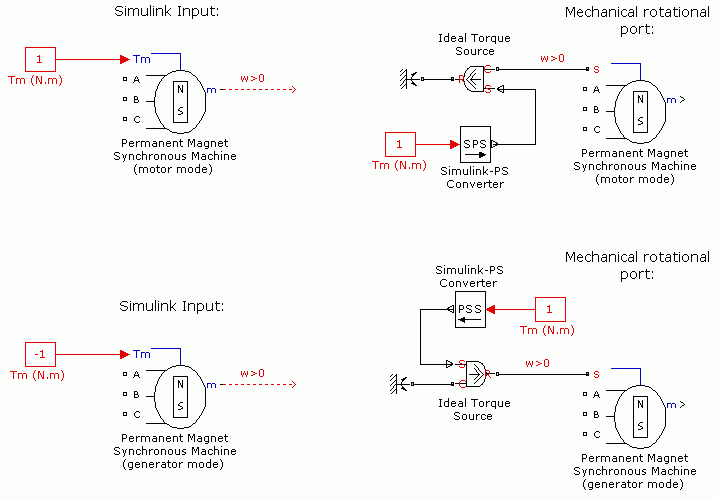
Permanent Magnet Synchronous Machine

正弦波または台形波の逆起電力をもつ三相永久磁石同期機、正弦波の逆起電力をもつ五相永久磁石同期機

• 

ライブラリ:
Simscape / Electrical / Specialized Power Systems / Electrical Machines

説明

Permanent Magnet Synchronous Machine ブロックは、三相または五相の永久磁石同期機を実装します。固定子巻線は内部の中性点に Y 結線されます。

三相電動機では、逆起電力の波形は正弦波または台形波になります。回転子は、正弦波の電動機では円筒形または突極形になります。電動機が台形波の場合は、回転子は円筒形です。正弦波の逆起電力をもつ電動機用にプリセット モデルが用意されています。

五相電動機では、逆起電力の波形は正弦波、回転子は円筒形です。

Permanent Magnet Synchronous Machine ブロックは、発電機モードまたはモーター モードのいずれかで動作します。動作モードは機械トルクの符号によって決まります (モーター モードは正、発電機モードは負)。電動機の電気的な部分と機械的な部分は、それぞれ 2 次状態空間モデルで表されます。

正弦波モデルでは、固定子の永久磁石による磁束が正弦波であると仮定されます。これは、起電力が正弦波であることを意味します。

台形モデルでは、巻線配電と永久磁石による磁束によって 3 つの台形波の逆起電力波形が生成されると仮定されます。

三相正弦波モデルの電気システム

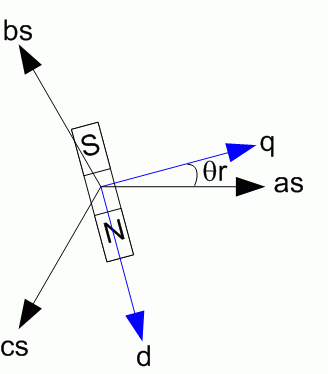
以下の方程式は、回転子の基準座標系 (qd 座標系) で表されています。回転子の基準座標系のすべての数量は固定子に関するものです。

$$\frac{d}{dt}{i}_d=\frac{1}{L_d}{v}_d-\frac{R}{L_d}{i}_d+\frac{L_q}{L_d}p{\omega }_m{i}_q$$

$$\frac{d}{dt}{i}_q=\frac{1}{L_q}{v}_q-\frac{R}{L_q}{i}_q-\frac{L_d}{L_q}p{\omega }_m{i}_d-\frac{\lambda p{\omega }_m}{L_q}$$

$$T_e=1.5p[\lambda i_q+(L_d-L_q)i_d{i}_q]$$

Lq、Ld	q 軸と d 軸のインダクタンス
R	固定子巻線の抵抗
iq、id	q 軸と d 軸の電流
vq、vd	q 軸と d 軸の電圧
ωm	回転子の角速度
λ	回転子の永久磁石による固定子相での誘起磁束の振幅
p	極対数
Te	電磁トルク

L_q インダクタンスと L_d インダクタンスは、回転子の突極性による相のインダクタンスと回転子の位置の関係を表します。たとえば、A 相と B 相の間 (C 相は開いたまま) で測定されるインダクタンスは以下で与えられます。

$$L_{ab}=L_d+L_q+\left(L_q-L_d\right)\cos \left(2{\theta }_e+\frac{\pi }{3}\right),$$

ここで、Θ_e は電気角を表します。

次の図は、相間インダクタンスの変動を回転子の電気角の関数で示したものです。

• 円筒形回転子の場合、相のインダクタンスに変動はありません。

  $$L_d=L_q=\frac{L_{ab}}{2}.$$

• 突極形回転子の場合、dq インダクタンスは以下で与えられます。

  $$L_d=\frac{\max (L_{ab})}{2}$$

  $$L_q=\frac{\min (L_{ab})}{2}$$

五相正弦波モデルの電気システム

以下の方程式は、拡張 Park 変換を使用した回転子の基準座標系 (q1d1 座標系と q2d2 座標系) で表されています。回転子の基準座標系のすべての数量は固定子に関するものです。

$$\frac{d}{dt}{i}_{d1}=\frac{1}{L}{v}_{d1}-\frac{R}{L}{i}_{d1}+\frac{L_q}{L}p{\omega }_m{i}_{q1}$$

$$\frac{d}{dt}{i}_{q1}=\frac{1}{L}{v}_{q1}-\frac{R}{L}{i}_{q1}-\frac{L_d}{L}p{\omega }_m{i}_{d1}-\frac{\lambda p{\omega }_m}{L}$$

$$\frac{d}{dt}{i}_{d2}=\frac{1}{L}{v}_{d2}-\frac{R}{L}{i}_{d2}$$

$$\frac{d}{dt}{i}_{q2}=\frac{1}{L}{v}_{q2}-\frac{R}{L}{i}_{q2}$$

$$T_e=2.5p\lambda i_{q1}$$

L	電機子のインダクタンス
R	固定子巻線の抵抗
iq1、id1	q1 軸と d1 軸の電流
vq1、vd1	q1 軸と d1 軸の電圧
iq2、id2	q2 軸と d2 軸の電流
vq2、vd2	q2 軸と d2 軸の電圧
ωm	回転子の角速度
λ	回転子の永久磁石による固定子相での誘起磁束の振幅
p	極対数
Te	電磁トルク

三相台形波モデルの電気システム

以下の方程式は、相の基準座標系 (abc 座標系) で表されています。相のインダクタンス L_s は一定であると仮定され、回転子の位置によって変動しないことに注意してください。

$$\begin{array}{c}\frac{d}{dt}{i}_a=\frac{1}{3L_s}\left(2v_{ab}+v_{bc}-3R_s{i}_a+\lambda p{\omega }_m\left(-2{\Phi }_a^{\prime }+{\Phi }_b^{\prime }+{\Phi }_c^{\prime }\right)\right)\\ \frac{d}{dt}{i}_b=\frac{1}{3L_s}\left(-v_{ab}+v_{bc}-3R_s{i}_b+\lambda p{\omega }_m\left({\Phi }_a^{\prime }-2{\Phi }_b^{\prime }+{\Phi }_c^{\prime }\right)\right)\\ \frac{d}{dt}{i}_c=-\left(\frac{d}{dt}{i}_a+\frac{d}{dt}{i}_b\right)\\ T_e=p\lambda \left({\Phi }_a^{\prime }\cdot i_a+{\Phi }_b^{\prime }\cdot i_b+{\Phi }_c^{\prime }\cdot i_c\right)\end{array}$$

Ls	固定子巻線のインダクタンス
R	固定子巻線の抵抗
ia、ib、ic	a 相、b 相、c 相の電流
Φa'、Φb'、Φc'	a 相、b 相、c 相の起電力 (磁束 λ の振幅に対する pu 値)
vab、vbc	ab と bc の相関の電圧
ωm	回転子の角速度
λ	回転子の永久磁石による固定子相での誘起磁束の振幅
p	極対数
Te	電磁トルク

起電力 Φ^' は以下で表されます。

機械システム

$$\begin{array}{c}\frac{d}{dt}{\omega }_m=\frac{1}{J}\left(T_e-T_f-F{\omega }_m-T_m\right)\\ \frac{d\theta }{dt}={\omega }_m\end{array}$$

J	回転子と負荷を合わせた慣性
F	回転子と負荷を合わせた粘性摩擦
θ	回転子の角度位置
Tm	シャフトの機械トルク
Tf	シャフトの静止摩擦トルク
ωm	回転子の角速度 (機械速度)

例

6 ステップ インバーターによって電力が供給されるブラシレス DC モーター

この例では、定格値が 1 kW 3000 rpm で、速度が制御される台形波 PMSM モーターの 6 ステップ スイッチ オン モードの使用法を示します。

• モデルを開く

制限と仮定

離散システムで Permanent Magnet Synchronous Machine ブロックを使用する場合、小さな寄生抵抗負荷 (電動機の端子に接続) を使用して数値振動の発生を避ける必要が生じることがあります。サンプル時間が大きいと、必要な負荷が大きくなります。最小抵抗負荷はサンプル時間に比例します。最小負荷は、60 Hz のシステムでタイム ステップが 25 μs の場合に電動機のノミナル電力の約 2.5% と覚えておいてください。たとえば、50 μs のサンプル時間で離散化された電力システムの 200 MVA の永久磁石同期機には、約 5% にあたる 10 MW の抵抗負荷が必要です。サンプル時間を 20 μs に減らせば、抵抗負荷は 4 MW で十分です。

Permanent Magnet Synchronous Machine ブロックでは、固定子と回転子に鉄の飽和がない線形磁気回路を仮定しています。この仮定は、永久磁石同期機でよく見られる大きなエア ギャップによるものです。

端子

入力

Tm — 機械トルク

スカラー

電動機のシャフトの機械トルク。Permanent Magnet Synchronous Machine ブロックは一般にモーターとして使用されるため、この入力端子は通常は正です。ブロックを発電機モードで使用する場合は、負のトルク入力を適用できます。

依存関係

この端子を有効にするには、[Mechanical input] を [Torque Tm] に設定します。

w — 電動機の速度

スカラー

電動機の速度 (rad/s)。

依存関係

この端子を有効にするには、[Mechanical input] を [Speed w] に設定します。

出力

m — 電動機の内部の測定値

13 要素ベクトル | 16 要素ベクトル

測定信号を含むベクトル。ブロックは [Number of phases] が 3 に設定されている場合は 13 要素ベクトル、[Number of phases] が 5 に設定されている場合は 16 要素ベクトルを返します。使用できる信号は、選択したモデルによって異なります。Simulink^® ライブラリで提供される Bus Selector ブロックを使用して、これらの信号を逆多重化できます。信号には以下が含まれます。

名前	定義	単位	モデル
ias	固定子電流 is_a	A	すべて
ibs	固定子電流 is_b	A	すべて
ics	固定子電流 is_c	A	すべて
ids	固定子電流 is_d	A	五相正弦波
ies	固定子電流 is_e	A	五相正弦波
iqs	固定子電流 is_q	A	三相正弦波
ids	固定子電流 is_d	A	三相正弦波
iqs1	固定子電流 is_q1	A	五相正弦波
ids1	固定子電流 is_d1	A	五相正弦波
iqs2	固定子電流 is_q2	A	五相正弦波
ids2	固定子電流 is_d2	A	五相正弦波
vqs	固定子電圧 Vs_q	V	三相正弦波
vds	固定子電圧 Vs_d	V	三相正弦波
vqs1	固定子電圧 Vs_q1	V	五相正弦波
vds1	固定子電圧 Vs_d1	V	五相正弦波
vqs2	固定子電圧 Vs_q2	V	五相正弦波
vds2	固定子電圧 Vs_d2	V	五相正弦波
ea	位相逆起電力 e_a	V	三相台形波
eb	位相逆起電力 e_b	V	三相台形波
ec	位相逆起電力 e_c	V	三相台形波
ha	ホール効果信号 h_a*	論理 (0 または 1)	三相の正弦波と台形波
hb	ホール効果信号 h_b*	論理 (0 または 1)	三相の正弦波と台形波
hc	ホール効果信号 h_c*	論理 (0 または 1)	三相の正弦波と台形波
w	回転子速度 wm	rad/s	すべて
theta	回転子角度 thetam	rad	すべて
Te	電磁トルク Te	N.m	すべて

ホール効果信号は、逆起電力の位置の論理指標を提供します。この信号は、電源スイッチを直接制御するのに非常に便利です。線間電圧のゼロクロッシングのたびに状態が変化します。これらの信号は、スイッチに適用する前に復号化する必要があります。

保存

S — 電動機の回転シャフト

機械回転

機械回転端子。電動機の回転シャフトを表します。

依存関係

この端子を有効にするには、[Mechanical input] を [Mechanical rotational port] に設定します。

A — A 相の電気端子

特定用途向けの電気

A 相の電気端子に関連付けられた特定用途向けの電気量保存端子。

B — B 相の電気端子

特定用途向けの電気

B 相の電気端子に関連付けられた特定用途向けの電気量保存端子。

C — C 相の電気端子

特定用途向けの電気

C 相の電気端子に関連付けられた特定用途向けの電気量保存端子。

パラメーター

Configuration

Number of phases — 電動機モデルの相数

3 (既定値) | 5

三相電動機モデルまたは五相電動機モデルのいずれかを選択します。

Back EMF waveform — 起電力

Sinusoidal (既定値) | Trapezoidal

起電力を [Sinusoidal] と [Trapezoidal] から選択します。

依存関係

このパラメーターを有効にするには、[Number of phases] を [3] に設定します。

Rotor type — 回転子タイプ

Round (既定値) | Salient-pole

回転子を [Salient-pole] と [Round] から選択します。

依存関係

このパラメーターを有効にするには、[Number of phases] を [3] に設定し、[Back EMF waveform] を [Sinusoidal] に設定します。

Mechanical input — 入力のタイプ

Torque Tm (既定値) | Speed w | Mechanical rotational port

シャフトに加えられるトルク、回転子の速度、または Simscape™ 機械回転端子で表される電動機のシャフトのいずれによって入力が供給されるかを選択します。

トルク入力 (N.m) を指定して Tm 端子を表示するには、[Torque Tm] を選択します。電動機の慣性 J、および加えられる機械トルク Tm と内部の電磁トルク Te の差によって、電動機の速度が決まります。機械トルクの符号の規則は、速度が正のときのものです。正のトルク信号はモーター モードを示し、負の信号は発電機モードを示します。

速度入力 (rad/s) を指定して w 端子を表示するには、[Speed w] を選択します。電動機の速度が課され、モデルの機械部分 (慣性 J) は無視されます。速度を機械入力として使用することで、2 つの電動機間の機械的な接続をモデル化できます。

次の図は、スティッフなシャフトの相互接続をモーターと発電機のセットでモデル化する方法を示しています。ここでは、電動機 2 の摩擦トルクが無視されています。電動機 1 (モーター) の速度出力が電動機 2 (発電機) の速度入力に接続され、電動機 2 の電磁トルク出力 Te が電動機 1 の機械トルク Tm に加えられます。係数 Kw で両方の電動機の速度の単位 (pu または rad/s) とギア ボックス比 w2/w1 が考慮されます。係数 KT で両方の電動機のトルクの単位 (pu または N.m) と電動機の定格が考慮されます。また、電動機 2 では慣性 J2 が無視されるため、電動機 1 の慣性 J1 に J2 が加算されています。

Simscape 機械回転端子を表示して、機械回転端子をもつ他の Simscape ブロックに電動機のシャフトを接続できるようにするには、[Mechanical rotational port] を選択します。

次の図は、Simscape ライブラリの Ideal Torque Source ブロックを電動機のシャフトに接続してモーター モードまたは発電機モードで電動機を表す方法を示しています。

Preset model — 電気と機械のパラメーター

No (既定値) | 01: 0.8 Nm 300 Vdc 3000 RPM - 0.8 Nm | 02: 1.7 Nm 300 Vdc 3750 RPM - 1.7 Nm | ...

さまざまな永久磁石同期モーターのトルク (N.m)、DC 母線電圧 (V)、定格速度 (rpm)、連続停動トルク (N.m) の定格について、あらかじめ決められた電気と機械のパラメーター。

いずれかのプリセット モデルを選択すると、対応する電気と機械のパラメーターがダイアログ ボックスのエントリに読み込まれます。プリセット モデルを使用しない場合やプリセット モデルのパラメーターの一部を変更する場合は、[No] (既定の設定) を選択します。

使用できるプリセット モデルは次のとおりです。

• No

• 01: 0.8 Nm 300 Vdc 3000 RPM - 0.8 Nm

• 02: 1.7 Nm 300 Vdc 3750 RPM - 1.7 Nm

• 03: 2.8 Nm 300 Vdc 4250 RPM - 3.2 Nm

• 04: 6 Nm 300 Vdc 4500 RPM - 6 Nm

• 05: 8 Nm 300 Vdc 2000 RPM - 10 Nm

• 06: 10 Nm 300 Vdc 2300 RPM - 14.2 Nm

• 07: 20 Nm 300 Vdc 2200 RPM - 33.9 Nm

• 08: 24 Nm 300 Vdc 2300 RPM - 41.4 Nm

• 09: 7.14 Nm 560 Vdc 5000 RPM - 8.3 Nm

• 10: 7.71 Nm 560 Vdc 5000 RPM - 10.2 Nm

• 11: 26.13 Nm 560 Vdc 3000 RPM - 27.3 Nm

• 12: 35.17 Nm 560 Vdc 3000 RPM - 37.4 Nm

• 13: 42.09 Nm 560 Vdc 3000 RPM - 45.6 Nm

• 14: 67.27 Nm 560 Vdc 1700 RPM - 70.2 Nm

• 15: 87.75 Nm 560 Vdc 3000 RPM - 97.96 Nm

• 16: 111 Nm 560 Vdc 3000 RPM - 126 Nm

プリセット モデルを選択すると、ダイアログ ボックスの [Parameters] タブにある電気と機械のパラメーターは無効になります。特定のプリセット モデルから始めて電動機のパラメーターを変更するには、次のようにします。

1. パラメーターを初期化するプリセット モデルを選択します。

2. [Preset model] を [No] に変更します。このとき、[Parameters] タブの電動機のパラメーターは変わりません。

3. 電動機のパラメーターを変更し、[Apply] をクリックします。

依存関係

このパラメーターを有効にするには、[Number of phases] を 5 に設定するか、[Number of phases] を 3、[Back EMF waveform] を [Sinusoidal] に設定します。

Use signal names to identify bus labels — 信号名または信号定義で識別

off (既定値) | on

オンの場合、母線のラベルの識別に測定出力で信号名が使用されます。母線の信号ラベルを英数字のみにする必要があるアプリケーションでは、このオプションをオンにします。

オフの場合、母線のラベルの識別に測定出力で信号定義が使用されます。一部の Simulink アプリケーションと互換性がない英数字以外の文字がラベルに含まれます。

パラメーター

Stator phase resistance Rs (Ohm) — 固定子相抵抗

0.0485 (既定値) | 正のスカラー

固定子相抵抗 Rs (Ω)。

Stator phase inductance Ls (H) — 固定子相-中性点間インダクタンス

8.5e-3 (既定値) | 正のスカラー

台形波モデルの固定子相-中性点間インダクタンス Ls (H)。

依存関係

このパラメーターを有効にするには、[Number of phases] を 3、[Back EMF waveform] を [Trapezoidal] に設定します。

Inductances [ Ld(H) Lq(H) ] — 相-中性点間インダクタンス

[8.5e-3,8.5e-3] (既定値) | 2 要素ベクトル

突極形回転子をもつ正弦波モデルの d 軸と q 軸の相-中性点間インダクタンス Ld (H) と Lq (H)。

依存関係

このパラメーターを有効にするには、[Number of phases] を 3、[Back EMF waveform] を [Sinusoidal]、[Rotor type] を [Salient-pole] に設定します。

Armature inductance (H) — 正弦波モデルの電機子インダクタンス

0.000395 (既定値) | 正のスカラー

円筒形回転子をもつ正弦波モデルの電機子インダクタンス。Ld は Lq と等しくなります。

依存関係

このパラメーターを有効にするには、[Number of phases] を 3、[Back EMF waveform] を [Sinusoidal]、[Rotor type] を [Round] に設定します。

Specify — 電動機定数

Flux linkage established by magnets (V.s) (既定値) | Voltage Constant (V_peak L-L / krpm) | Torque Constant (N.m / A_peak)

ブロック パラメーター化の電動機定数。定数を選択したら、その値を該当するパラメーターのフィールドに入力できます。他の 2 つのパラメーターは無効になります。

Flux linkage — 一定磁束

0.1194 (既定値) | 正のスカラー

磁石によって固定子巻線で誘起される極対ごとの一定磁束 λ (Wb)。

依存関係

このパラメーターを有効にするには、[Specify] を [Flux linkage established by magnets (V.s)] に設定します。

Voltage constant — ピーク線間電圧

86.6271 (既定値) | 正のスカラー

1000 rpm あたりのピーク線間電圧。この電圧は、電動機が発電機として 1000 rpm で駆動されたときのピーク開回路電圧を表します。

依存関係

このパラメーターを有効にするには、[Specify] を [Voltage Constant (V_peak L-L / krpm)] に設定します。

トルク定数 — アンペアあたりのトルク定数

0.7164 (既定値) | 正のスカラー

アンペアあたりのトルク定数。この定数は、電流と逆起電力の間の完全な同期を提供するインバーターによって電動機が駆動されると仮定したものです。

• 正弦波モデル: 正弦波電流が仮定されます。

• 台形波モデル: 矩形波電流が仮定されます。

依存関係

このパラメーターを有効にするには、[Specify] を [Torque Constant (N.m / A_peak)] に設定します。

Back EMF flat area (degrees) — フラット トップの幅

120 (既定値) | 正のスカラー

台形波電動機の起電力の半分の周期におけるフラット トップの幅 Φ^' (度)。

依存関係

このパラメーターを有効にするには、[Number of phases] を 3、[Back EMF waveform] を [Trapezoidal] に設定します。

Inertia, viscous damping, pole pairs, static friction [ J(kg.m^2) F(N.m.s) p() Tf(N.m)] — 機械パラメーター

[0.0027 0.0004924 4 0] (既定値) | 3 要素ベクトル | 4 要素ベクトル

電動機と負荷を合わせた慣性係数 J (kg.m²)、複合の粘性摩擦係数 F (N.m.s)、極対数 p、シャフトの静止摩擦 T_f (N.m)。ベクトルの 4 番目の値 (静止摩擦) が指定されていない場合、ブロックはこの値を 0 であると見なします。

依存関係

このパラメーターを有効にするには、[Mechanical input] を [Torque Tm] または [Mechanical rotational port] に設定します。

Pole pairs p () — 極対数

4 (既定値) | 正のスカラー

極対数 p。

依存関係

このパラメーターを有効にするには、[Mechanical input] を [Speed w] に設定します。

Initial conditions [ wm(rad/s) thetam(deg) ia,ib(A) ] — 三相電動機の初期状態

[0,0, 0,0] (既定値) | 4 要素ベクトル

三相電動機の機械速度 (rad/s)、機械的角度 Θ_m (度)、瞬時固定子電流 (A) [w_m, Θ_m, i_a, i_b]。

固定子は Y 結線であり、中性点が絶縁されているため、三相電動機の電流 i_c は i_c = -i_a-i_b で与えられます。

依存関係

このパラメーターを有効にするには、[Number of phases] を [3] に設定します。

Initial conditions [ wm(rad/s) thetam(deg) ia,ib,ic,id(A) ] — 五相電動機の初期状態

[0 0 0 0 0 0] (既定値) | 6 要素ベクトル

五相電動機の機械速度 (rad/s)、機械的角度 Θ_m (度)、瞬時固定子電流 (A) [w_m, Θ_m, i_a, i_b, i_c, i_d]。

固定子は Y 結線であり、中性点が絶縁されているため、五相電動機の電流 i_e は i_e = -i_a -i_b -i_c -i_d で与えられます。

依存関係

このパラメーターを有効にするには、[Number of phases] を [5] に設定します。

Rotor flux position when theta = 0 — 回転子磁束の基準位置

90 degrees behind phase A axis (modified Park) (既定値) | Aligned with phase A axis (original Park)

A 相の軸を基準とした回転子磁束の基準位置。

以下で表される回転子の基準位置を選択するには、[90 degrees behind phase A axis (modified Park)] を選択します。

相誘導が theta = 0 で最大になるため、ベクトル制御には修正された Park 変換 [4] の方が便利です。

以下で表される回転子の基準位置を選択するには、[Aligned with phase A axis (original Park)] を選択します。

Advanced

[Advanced] タブを有効にするには、powergui ブロックの [Simulation type] パラメーターを [Discrete] に設定し、[Preferences] タブで [Automatically handle discrete solver and Advanced tab solver settings of blocks] パラメーターをオフにします。

Discrete solver model — 積分法

Trapezoidal non iterative (既定値) | Trapezoidal robust | Backward Euler robust

ブロックで使用される積分法。

powergui ブロックで [Automatically handle discrete solver and Advanced tab solver settings of blocks] パラメーターをオンにすると、離散ソルバー モデルは自動的に [Trapezoidal robust] に設定されます。

[Trapezoidal non iterative] では、シミュレーションの安定性を維持するために、無視できないシャント負荷を電動機の端子に追加する必要があり、モデルで電動機の数が増えるとシミュレーションが収束せずに停止することがあります。

[Trapezoidal robust] と [Backward Euler robust] では、寄生負荷を使用する必要はありません。誘導性回路 (電動機と直列に接続された回路ブレーカーなど) に接続された電動機の位相的な誤りをなくすには、ノミナル電力の 0.01% のごくわずかな内部負荷を電動機でモデル化します。

[Trapezoidal robust] は、特に大きなサンプル時間でモデルをシミュレーションする場合に [Backward Euler robust] より少しだけ精度が高くなります。[Trapezoidal robust] では、無負荷状態において、電動機の電圧にわずかな減衰数値振動が生じる可能性がありますが、[Backward Euler robust] では振動は生じず、精度が維持されます。

ご利用の用途で使用する手法の詳細については、電気回路の離散化によるシミュレーションを参照してください。

サンプル時間 (継承は -1) — ブロックで使用されるサンプル時間

-1 (既定値) | スカラー

ブロックで使用されるサンプル時間。powergui ブロックで指定されたサンプル時間を継承するには、このパラメーターを -1 (既定の設定) に設定します。

参照

[1] Grenier, D., L.-A. Dessaint, O. Akhrif, Y. Bonnassieux, and B. LePioufle. “Experimental Nonlinear Torque Control of a Permanent Magnet Synchronous Motor Using Saliency.” IEEE^® Transactions on Industrial Electronics, Vol. 44, No. 5, October 1997, pp. 680-687.

[2] Toliyat, H.A. “Analysis and Simulation of Multi-Phase Variable Speed Induction Motor Drives Under Asymmetrical Connections.” Applied Power Electronics Conference and Exposition, Vol. 2, March 1996, pp. 586-592.

[3] Beaudart, F., F. Labrique, E. Matagne, D. Telteux, and P. Alexandre. “Control under normal and fault tolerant operation of multiphase SMPM synchronous machines with mechanically and magnetically decoupled phases.” International Conference on Power Engineering, Energy and Electrical Drives, March 2009, pp. 461-466.

[4] Krause, P.C., O. Wasynczuk, and S.D. Sudhoff. Analysis of Electric Machinery and Drive Systems. IEEE Press, 2002.

拡張機能

C/C++ コード生成
Simulink® Coder™ を使用して C および C++ コードを生成します。

バージョン履歴

R2006a より前に導入