Main Content

パラメーター コンフィギュレーション ファイルの使用

解析用にパラメーターを変数として指定する場合、パラメーター テーブルを使用することも、MATLAB® コード ファイルでパラメーター コンフィギュレーションを定義することもできます。また、パラメーター テーブルからパラメーター コンフィギュレーション ファイルをエクスポートすることもできます。詳細は、パラメーター制約の MATLAB コード ファイルへの格納を参照してください。

この例では、MATLAB コード ファイルでパラメーター コンフィギュレーションを定義する方法を説明します。パラメーター テーブルを使用してこれらのパラメーター コンフィギュレーションを定義する方法を説明する例は、パラメーター テーブルの使用を参照してください。

パラメーター コンフィギュレーション ファイルのテンプレート

Simulink® Design Verifier™ ソフトウェアでは、開始点として役立つ注釈付きテンプレートを提供しています。

matlabroot/toolbox/sldv/sldv/sldv_params_template.m

パラメーター コンフィギュレーション ファイルを作成するには、テンプレートをコピーしてそのコピーを編集します。テンプレートではコメントにより、パラメーター コンフィギュレーションを定義するための構文が説明されています。

モデルを解析する前にパラメーター コンフィギュレーション ファイルをモデルと関連付けるには、[コンフィギュレーション パラメーター] ダイアログ ボックスの [Design Verifier] 、 [パラメーターとバリアント] ペインで、[パラメーター コンフィギュレーション ファイル] フィールドにファイル名を入力します。

パラメーター コンフィギュレーション ファイル内の構文

入力変数として扱うパラメーターと同じ名前をもつ複数のフィールドを含む構造体を使用して、パラメーター コンフィギュレーションを指定します。

たとえば、[ゲイン] パラメーターおよび [定数値] パラメーターである、m と b を制約するとします。これを次のモデルで示します。

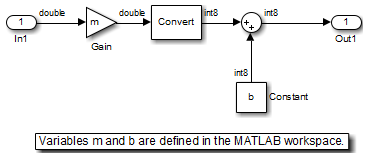
モデルを開くと、コールバック関数 PreLoadFcn が MATLAB ワークスペースで m および b を定義します。

  • m は 5 に設定されます。

  • b は値が 5 の int8 型の Simulink.Parameter オブジェクトとして設定されます。

パラメーター コンフィギュレーション ファイルで、m および b の制約を指定します。

params.b = int8([4 10]);
params.m = {};

このファイルでは次が指定されています。

  • b は 4 ～ 10 の 8 ビット符号付き整数です。制約タイプは、MATLAB ワークスペースのパラメーター b のタイプと一致しなければなりません。この例では int8 です。

  • m はどの値にも制約されません。

Sldv.Point コンストラクターを使用して点を指定します。これは引数として単一値を受け入れます。Sldv.Interval コンストラクターを使用して間隔を指定します。2 つの引数 (間隔の上限と下限) が必要です。オプションで、間隔の端点を含めるか排除するかを指定する 3 番目の入力引数として次のいずれかの値を指定できます。

  • '()' — 開区間を定義します。

  • '[]' — 閉区間を定義します。

  • '(]' — 左開右閉区間を定義します。

  • '[)' — 左閉右開区間を定義します。

メモ

既定では、この引数を省略すると、Simulink Design Verifier は閉区間であるとみなします。

次の例では、m を 3 に、b を閉区間 [0, 10] 内の任意の値に制約します。

params.m = Sldv.Point(3);
params.b = Sldv.Interval(0, 10);

パラメーターがスカラーの場合、コンストラクターを省略して代わりに単一値または 2 要素ベクトルを指定することができます。たとえば、前の例は次のように指定できます。

params.m = 3;
params.b = [0 10];

メモ

入力パラメーターに制約がないことを示すには、params.m = {} または params.m = [] を指定します。解析ではこのパラメーターを任意の入力として処理します。

cell 配列を使用して単一のパラメーターに複数の制約を指定することができます。この場合、解析では制約が論理 OR 演算を使用して組み合わされます。

次の例では、m を 3 または 5 に制約し、b を閉区間 [0, 10] 内の任意の値に制約します。

params.m = {3, 5};
params.b = [0 10];

構造体のサイズを拡張して、複数のパラメーター セットを指定できます。たとえば、次の例では 1 行 2 列の構造体を使用して2 つのパラメーターのセットを定義します。

params(1).m = {3, 5};
params(1).b = [0 10];

params(2).m = {12, 15, Sldv.Interval(50, 60, '()')};
params(2).b = 5;

最初のパラメーターのセットは、m を 3 または 5 に制約し、b を閉区間 [0, 10] 内の任意の値に制約します。2 番目のパラメーターのセットは、m を 12、15、または開区間 (50, 60) 内の任意の値に制約し、b を 5 に制約します。