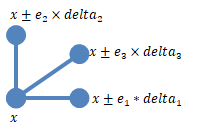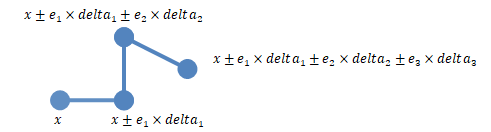sbioelementaryeffects
Perform global sensitivity analysis (GSA) by computing elementary effects (requires Statistics and Machine Learning Toolbox)
Since R2021b
Syntax
Description
elementaryEffectsResults = sbioelementaryeffects(modelObj,params,observables)modelObj
by computing elementary effects of observables with respect to
individual model quantities or parameters specified in params.
elementaryEffectsResults = sbioelementaryeffects(modelObj,params,observables,Name=Value)
Examples
Load the tumor growth model.
sbioloadproject tumor_growth_vpop_sa.sbprojGet a variant with estimated parameters and the dose to apply to the model.
v = getvariant(m1);
d = getdose(m1,'interval_dose');Get the active configset and set the tumor weight as the response.
cs = getconfigset(m1);
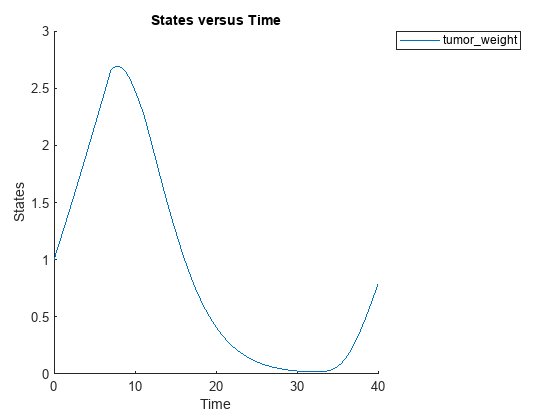
cs.RuntimeOptions.StatesToLog = 'tumor_weight';Simulate the model and plot the tumor growth profile.
sbioplot(sbiosimulate(m1,cs,v,d));
Perform global sensitivity analysis (GSA) on the model to find the model parameters that the tumor growth is sensitive to.
First, define model parameters of interest, which are involved in the pharmacodynamics of the tumor growth. Define the model response as the tumor weight.
modelParamNames = {'L0','L1','w0','k1'};
outputName = 'tumor_weight';Then perform GSA by computing the elementary effects using sbioelementaryeffects. Use 100 as the number of samples and set ShowWaitBar to true to show the simulation progress.
rng('default');
eeResults = sbioelementaryeffects(m1,modelParamNames,outputName,Variants=v,Doses=d,NumberSamples=100,ShowWaitbar=true);Show the median model response, the simulation results, and a shaded region covering 90% of the simulation results.
plotData(eeResults,ShowMedian=true,ShowMean=false);
![Figure contains an axes object. The axes object with xlabel time, ylabel [Tumor Growth].tumor indexOf w baseline eight contains 12 objects of type line, patch. These objects represent model simulation, 90.0% region, median value.](../../examples/simbio/win64/PerformGSAByComputingElementaryEffectsExample_02.png)
You can adjust the quantile region to a different percentage by specifying Alphas for the lower and upper quantiles of all model responses. For instance, an alpha value of 0.1 plots a shaded region between the 100*alpha and 100*(1-alpha) quantiles of all simulated model responses.
plotData(eeResults,Alphas=0.1,ShowMedian=true,ShowMean=false);
![Figure contains an axes object. The axes object with xlabel time, ylabel [Tumor Growth].tumor indexOf w baseline eight contains 12 objects of type line, patch. These objects represent model simulation, 80.0% region, median value.](../../examples/simbio/win64/PerformGSAByComputingElementaryEffectsExample_03.png)
Plot the time course of the means and standard deviations of the elementary effects.
h = plot(eeResults);
% Resize the figure.
h.Position(:) = [100 100 1280 800];![Figure contains 8 axes objects. Axes object 1 with xlabel time, ylabel std. of effects k1 contains an object of type line. Axes object 2 with xlabel time, ylabel mean of effects k1 contains an object of type line. Axes object 3 with ylabel std. of effects w0 contains an object of type line. Axes object 4 with ylabel mean of effects w0 contains an object of type line. Axes object 5 with ylabel std. of effects L1 contains an object of type line. Axes object 6 with ylabel mean of effects L1 contains an object of type line. Axes object 7 with title sensitivity output [Tumor Growth].tumor_weight, ylabel std. of effects L0 contains an object of type line. Axes object 8 with title sensitivity output [Tumor Growth].tumor_weight, ylabel mean of effects L0 contains an object of type line.](../../examples/simbio/win64/PerformGSAByComputingElementaryEffectsExample_04.png)
The mean of effects explains whether variations in input parameter values have any effect on the tumor weight response. The standard deviation of effects explains whether the sensitivity change is dependent on the location in the parameter domain.
From the mean of effects plots, parameters L1 and w0 seem to be the most sensitive parameters to the tumor weight before the dose is applied at t = 7. But, after the dose is applied, k1 and L0 become more sensitive parameters and contribute most to the after-dosing stage of the tumor weight. The plots of standard deviation of effects show more deviations for the larger parameter values in the later stage (t > 35) than for the before-dose stage of the tumor growth.
You can also display the magnitudes of the sensitivities in a bar plot. Each color shading represents a histogram representing values at different times. Darker colors mean that those values occur more often over the whole time course.
bar(eeResults);
![Figure contains an axes object. The axes object with title sensitivity output [Tumor Growth].tumor_weight, xlabel elementary effects, ylabel sensitivity input contains 18 objects of type patch, line. These objects represent mean, standard deviation.](../../examples/simbio/win64/PerformGSAByComputingElementaryEffectsExample_05.png)
You can also plot the parameter grids and samples used to compute the elementary effects.
plotGrid(eeResults)
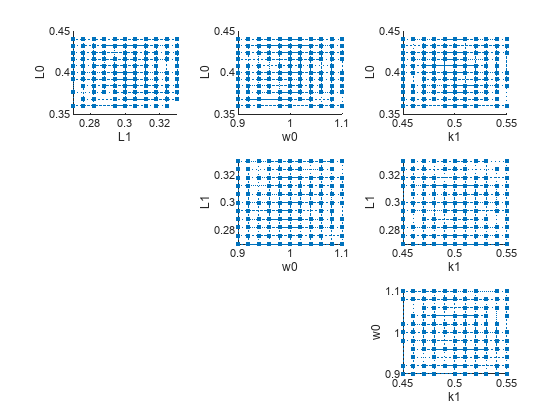
You can specify more samples to increase the accuracy of the elementary effects, but the simulation can take longer to finish. Use addsamples to add more samples.
eeResults2 = addsamples(eeResults,200);
The SimulationInfo property of the result object contains various information for computing the elementary effects. For instance, the model simulation data (SimData) for each simulation using a set of parameter samples is stored in the SimData field of the property. This field is an array of SimData objects.
eeResults2.SimulationInfo.SimData
SimBiology SimData Array : 1500-by-1 Index: Name: ModelName: DataCount: 1 - Tumor Growth Model 1 2 - Tumor Growth Model 1 3 - Tumor Growth Model 1 ... 1500 - Tumor Growth Model 1
You can find out if any model simulation failed during the computation by checking the ValidSample field of SimulationInfo. In this example, the field shows no failed simulation runs.
all(eeResults2.SimulationInfo.ValidSample)
ans = logical
1
You can add custom expressions as observables and compute the elementary effects of the added observables. For example, you can compute the effects for the maximum tumor weight by defining a custom expression as follows.
% Suppress an information warning that is issued. warnSettings = warning('off', 'SimBiology:sbservices:SB_DIMANALYSISNOTDONE_MATLABFCN_UCON'); % Add the observable expression. eeObs = addobservable(eeResults2,'Maximum tumor_weight','max(tumor_weight)','Units','gram');
Plot the computed simulation results showing the 90% quantile region.
h2 = plotData(eeObs,ShowMedian=true,ShowMean=false); h2.Position(:) = [100 100 1500 800];
![Figure contains 2 axes objects. Axes object 1 with ylabel Maximum tumor_weight contains 12 objects of type line, patch. One or more of the lines displays its values using only markers These objects represent model simulation, 90.0% region, median value. Axes object 2 with xlabel time, ylabel [Tumor Growth].tumor_weight contains 12 objects of type line, patch. These objects represent model simulation, 90.0% region, median value.](../../examples/simbio/win64/PerformGSAByComputingElementaryEffectsExample_07.png)
You can also remove the observable by specifying its name.
eeNoObs = removeobservable(eeObs,'Maximum tumor_weight');Restore the warning settings.
warning(warnSettings);
Input Arguments
SimBiology model, specified as a SimBiology model object.
Names of model parameters, species, or compartments, specified as a character vector, string, string vector, or cell array of character vectors.
Example: ["k1","k2"]
Data Types: char | string | cell
Model responses, specified as a character vector, string, string vector, or cell
array of character vectors. Specify the names of species, parameters, compartments, or
observables.
Example: "tumor_growth"
Data Types: char | string | cell
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: eeResults =
sbioelementaryeffects(modelObj,params,observables,StopTime=10) specifies to use
a stop time of 10.
Parameter bounds, specified as a numeric matrix with two columns. The first column contains
the lower bounds and the second column contains the upper
bounds. The number of rows must be equal to the number of
parameters in params.
If a parameter has a nonzero value, the default bounds are ±10% of the value. If the
parameter value is zero, the default bounds are [0 1].
Example: [0.5 5]
Data Types: double
Doses to use during model simulations, specified as a ScheduleDose or
RepeatDose object or a vector of
dose objects.
Variants to apply before model simulations, specified as a variant object or vector of variant objects.
When you specify multiple variants with duplicate specifications for a property's value, the last occurrence for the property value in the array of variants is used during simulation.
Number of samples to compute elementary effects, specified as a positive integer.
The function requires (number of input model simulations to compute the elementary effects.params + 1) *
NumberSamples
Data Types: double
Method to select sample points to compute elementary effects, specified as
"chain" or "radial". The
"chain" point selection uses the Morris method [1]. The
"radial" point selection uses the Sohier method [2]. For details, see
Elementary Effects for Global Sensitivity Analysis.
Data Types: char | string
Discretization level of the parameter domain, specified as a positive even integer. This
parameter defines a grid of equidistant points in the parameter domain, where each dimension
is discretized using Gridlevel+1

For details, see Elementary Effects for Global Sensitivity Analysis.
Data Types: double
Step size for computing elementary effects, specified as a positive integer between 1 and
GridLevel. The step size is measured in terms of grid points
between neighboring points. The following figure shows examples of different grid delta
values.

For details, see Elementary Effects for Global Sensitivity Analysis.
Data Types: double
Flag to use the absolute values of elementary effects, specified as true or
false. By default, the function uses the absolute values of
elementary effects. Using nonabsolute values can average out when calculating the mean. For
details, see Elementary Effects for Global Sensitivity Analysis.
Data Types: logical
Method to generate parameter samples, specified as one of the following:
"lhs"— Use low-discrepancy Latin hypercube samples."random"— Use uniformly distributed random samples.
The function selects generated parameter samples by sampling the grid points.
Simulation stop time, specified as a nonnegative scalar. If you specify neither
StopTime nor OutputTimes, the function uses
the stop time from the active configuration set of the model. You cannot specify both
StopTime and OutputTimes.
Data Types: double
Simulation output times, specified as a numeric vector. The function computes the
elementary effects at these output time points. You cannot specify both
StopTime and OutputTimes. By default, the
function uses the reported time points of the first model simulation.
Example: [0 1 2 3.5 4 5 5.5]
Data Types: double
Flag to run model simulations in parallel, specified as true or
false. When the value is true and Parallel Computing Toolbox™ is available, the function runs simulations in parallel.
Data Types: logical
Flag to turn on model acceleration, specified as true or
false.
Data Types: logical
Method for interpolation of model responses to a common set of output times, specified as a character vector or string. The valid options follow.
Data Types: char | string
Flag to show the progress of model simulations by displaying a wait bar, specified
as true or false. By default, no wait bar is
displayed.
Data Types: logical
Output Arguments
Results containing means and standard deviations of elementary effects, returned as
a SimBiology.gsa.ElementaryEffects object. The object includes information
such as the mean and standard deviation of elementary effects as well as parameter
samples and model simulations used to compute the elementary effects.
More About
sbioelementaryeffects lets you assess global
sensitivity of a model response with respect to variations in model parameters.
Consider a simple case with one sensitivity input parameter P. The elementary effect EE of P with respect to a model response R is defined as follows.
Here, EEP(x) is the elementary effect of
P. R(x) and R(x+delta) are model
responses at a specific time or the values of observables, evaluated for parameter values
x and
x+delta.
In the general case of k sensitivity input parameters,
x is a vector of different parameter values,
x =
[v1,v2,v3,…,vk].
The elementary effect of the ith parameter is computed as follows.
Here, ei is the ith
canonical unit vector. Thus, calculating the elementary effects of all parameters
P1,P2,P3,…,Pk
requires k+1 model simulations.
The function provides two methods ('PointSelection') to select a set of k+1
points required to compute these elementary effects.
To get the mean and standard deviation of elementary effects, the function computes
N ('NumberSamples') elementary effects per parameter, which requires
N*(k+1) simulations. By
default, the function reports the mean and standard deviation of
absolute elementary effects of each parameter
P1,P2,P3,…,Pk.
The mean of elementary effects explains whether variations in parameter P have any effect on response R on average.
The standard deviation explains whether the sensitivity change is dependent on the location in the parameter domain.
The function uses the absolute elementary effects by default
because the elementary effects can average out when calculating the mean otherwise.
Optionally, you can set the 'AbsoluteEffects' name-value argument to false to get the
means and standard deviations of nonabsolute elementary effects.
The function reports the points used to compute elementary effects in the
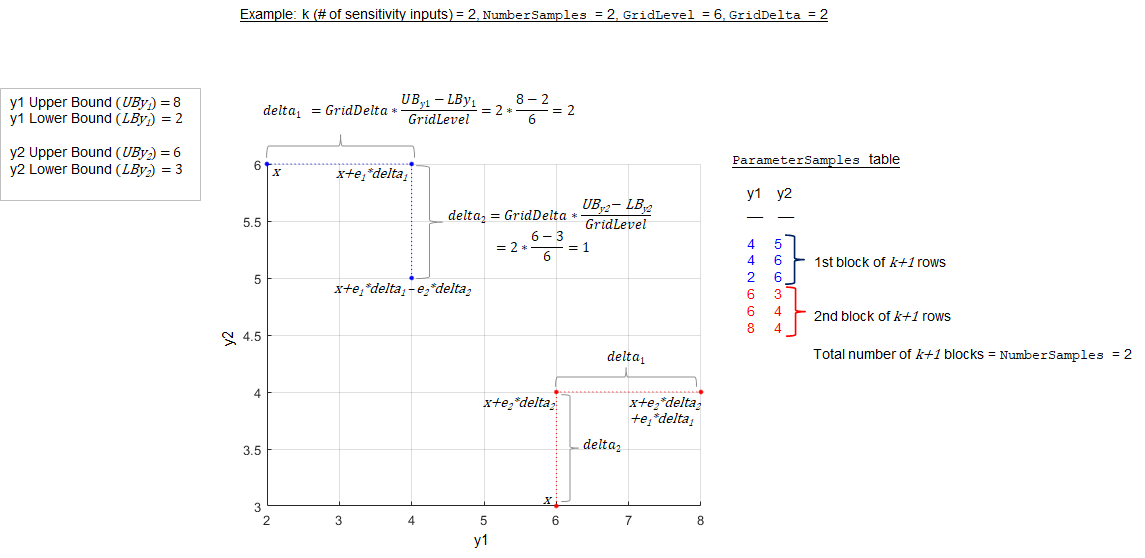
ParameterSamples property of the returned results object. Each block
of k+1 rows in the table of
ParameterSamples corresponds to the k+1 radial or chained points used
to compute the elementary effects. The SimulationInfo.SimData property
of the results object contains the corresponding model simulations. The function samples the
points from the parameter grid defined by 'GridLevel' and
'GridDelta'.
The following figure illustrates a simple case with two sensitivity inputs
(y1 and y2) with 'NumberSamples'
= 2 using the chain
'PointSelection' method.
References
[1] Morris, Max D. “Factorial Sampling Plans for Preliminary Computational Experiments.” Technometrics 33, no. 2 (May 1991): 161–74.
[2] Sohier, Henri, Jean-Loup Farges, and Helene Piet-Lahanier. “Improvement of the Representativity of the Morris Method for Air-Launch-to-Orbit Separation.” IFAC Proceedings Volumes 47, no. 3 (2014): 7954–59.
Version History
Introduced in R2021b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Web サイトの選択
Web サイトを選択すると、翻訳されたコンテンツにアクセスし、地域のイベントやサービスを確認できます。現在の位置情報に基づき、次のサイトの選択を推奨します:
また、以下のリストから Web サイトを選択することもできます。
最適なサイトパフォーマンスの取得方法
中国のサイト (中国語または英語) を選択することで、最適なサイトパフォーマンスが得られます。その他の国の MathWorks のサイトは、お客様の地域からのアクセスが最適化されていません。
南北アメリカ
- América Latina (Español)
- Canada (English)
- United States (English)
ヨーロッパ
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)