自己相関を使用した残差解析
この例では、信頼区間をもつ自己相関を使用してノイズ データの最小二乗近似の残差を解析する方法を示します。残差は近似モデルとそのデータの誤差を示します。信号とホワイト ノイズのモデルで信号に対して良い近似が得られている場合は、残差はホワイト ノイズのはずです。
加法性ホワイト ガウス ノイズを伴う 1 次の多項式 (直線) で構成されるノイズ データ セットを作成します。加法性ノイズは N(0,1) 分布に従う一連の無相関確率変数です。これは、すべての確率変数は平均 0 と分散 1 をもつことを意味します。再現性のある結果を得るために、乱数発生器を既定の状態に設定します。
x = -3:0.01:3;
rng default
y = 2*x+randn(size(x));
plot(x,y)
polyfit を使用して、ノイズ データに対する最小二乗の直線を求めます。元のデータを最小二乗近似に沿ってプロットします。
coeffs = polyfit(x,y,1); yfit = coeffs(2)+coeffs(1)*x; plot(x,y) hold on plot(x,yfit,'linewidth',2)

残差を求めます。残差の自己相関列を 50 ラグまで求めます。
residuals = y - yfit;
[xc,lags] = xcorr(residuals,50,'coeff');自己相関列の検査では自己相関の証拠があるかどうかが判断されます。言い換えると、サンプルの自己相関列がホワイト ノイズの自己相関列に似ているかどうかを判断します。残差の自己相関列がホワイト ノイズ過程の自己相関とよく似ている場合、信号が近似から外れたり残差に入ったりはしていないはずです。この例では、99% 信頼区間を使用します。信頼区間の構成には、サンプルの自己相関の値の分布を知る必要があります。また、対象分布上で、その間の確率が 0.99 になる棄却限界値を求める必要があります。この場合、分布はガウス分布なので逆相補誤差関数 erfcinv を使用することができます。この関数とガウス累積分布関数の逆関数との関係は、erfcinv のリファレンス ページで説明しています。
99% 信頼区間の棄却限界値を求めます。棄却限界値を使用して信頼限界の下限および上限を求めます。
conf99 = sqrt(2)*erfcinv(2*.01/2); lconf = -conf99/sqrt(length(x)); upconf = conf99/sqrt(length(x));
99% 信頼区間で自己相関列をプロットします。
figure stem(lags,xc,'filled') ylim([lconf-0.03 1.05]) hold on plot(lags,lconf*ones(size(lags)),'r','linewidth',2) plot(lags,upconf*ones(size(lags)),'r','linewidth',2) title('Sample Autocorrelation with 99% Confidence Intervals')

ゼロ ラグを除いて、サンプルの自己相関の値はホワイト ノイズ列の自己相関に対する 99% 信頼限界内にあります。このことから、残差がホワイト ノイズであることがわかります。より具体的には、残差がホワイト ノイズ過程の実現であることを棄却できません。
ノイズを含む正弦波で構成される信号を作成します。データは 1 kHz でサンプリングされます。正弦波の周波数は 100 Hz です。再現性のある結果を得るために、乱数発生器を既定の状態に設定します。
Fs = 1000;
t = 0:1/Fs:1-1/Fs;
rng default
x = cos(2*pi*100*t)+randn(size(t));離散フーリエ変換 (DFT) を使用して、100 Hz の正弦波の最小二乗近似を求めます。振幅の最小二乗推定は 100 Hz に対応する DFT 係数の 2/N 倍です。ここで、N は信号の長さです。実数部は 100 Hz における余弦の振幅、虚数部は 100 Hz における正弦の振幅です。最小二乗近似は、正確な振幅をもつ余弦と正弦の和です。この例では、DFT ビン 101 は 100 Hz に対応します。
xdft = fft(x); ampest = 2/length(x)*xdft(101); xfit = real(ampest)*cos(2*pi*100*t)+imag(ampest)*sin(2*pi*100*t); figure plot(t,x) hold on plot(t,xfit,'linewidth',2) axis([0 0.30 -4 4]) xlabel('Seconds') ylabel('Amplitude')

残差を求め、サンプルの自己相関列を 50 ラグまで算出します。
residuals = x-xfit;
[xc,lags] = xcorr(residuals,50,'coeff');99% の信頼区間で自己相関列をプロットします。
figure stem(lags,xc,'filled') ylim([lconf-0.03 1.05]) hold on plot(lags,lconf*ones(size(lags)),'r','linewidth',2) plot(lags,upconf*ones(size(lags)),'r','linewidth',2) title('Sample Autocorrelation with 99% Confidence Intervals')

ここでも、ゼロ ラグを除いて、サンプルの自己相関の値はホワイト ノイズ列の自己相関に対する 99% 信頼限界内にあることがわかります。このことから、残差がホワイト ノイズであることがわかります。より具体的には、残差がホワイト ノイズ過程の実現であることを棄却できません。
最後に、周波数 200 Hz、振幅 3/4 の正弦波をさらに加算します。100 Hz の正弦波の近似を求め、残差のサンプルの自己相関を求めます。
x = x+3/4*sin(2*pi*200*t);
xdft = fft(x);
ampest = 2/length(x)*xdft(101);
xfit = real(ampest)*cos(2*pi*100*t)+imag(ampest)*sin(2*pi*100*t);
residuals = x-xfit;
[xc,lags] = xcorr(residuals,50,'coeff');99% の信頼区間でサンプルの自己相関をプロットします。
figure stem(lags,xc,'filled') ylim([lconf-0.12 1.05]) hold on plot(lags,lconf*ones(size(lags)),'r','linewidth',2) plot(lags,upconf*ones(size(lags)),'r','linewidth',2) title('Sample Autocorrelation with 99% Confidence Intervals')
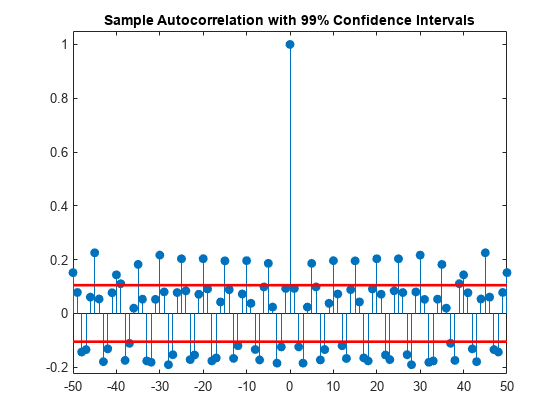
この場合、多くのラグにおいて、自己相関の値はホワイト ノイズの自己相関に対する 99% 信頼限界を明らかに超えています。ここでは、残差がホワイト ノイズ列であるという仮説を棄却できます。モデルはすべての信号を反映していないため、残差は信号とノイズで構成されていることを意味します。