このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

自己相関を使用した周期性の検出

信号での振動動作が予期される場合でも、測定の不確実性およびノイズがあると、そのような動作を検出することは困難なことがあります。

周期信号の自己相関列には、信号自体と同じ周期的特性があります。このため、自己相関はサイクルの存在を確認し、その期間を決定するのに役立ちます。

オフィス ビル内の温度計が収集した一連の温度データについて考えてみます。温度計は 4 か月間、30 分ごとに読み取りを行っています。データを読み込み、プロットします。温度の変動に集中できるよう、平均値を減算します。温度を摂氏に変換します。時間を日数で測定します。したがって、サンプル レートは 2 測定/時間 × 24 時間/日 = 48 測定/日です。

load officetemp

tempC = (temp-32)*5/9;

tempnorm = tempC-mean(tempC);

fs = 2*24;
t = (0:length(tempnorm) - 1)/fs;

plot(t,tempnorm)
xlabel('Time (days)')
ylabel('Temperature ( {}^\circC )')
axis tight

温度は振動しているように見えますが、サイクルの長さは簡単に読み取れません。

温度の自己相関を計算します。ゼロ ラグで値が 1 になるようにします。正負の遅れを 3 週間以内に制限します。この信号の二重の周期性に注意してください。

[autocor,lags] = xcorr(tempnorm,3*7*fs,'coeff');

plot(lags/fs,autocor)
xlabel('Lag (days)')
ylabel('Autocorrelation')
axis([-21 21 -0.4 1.1])

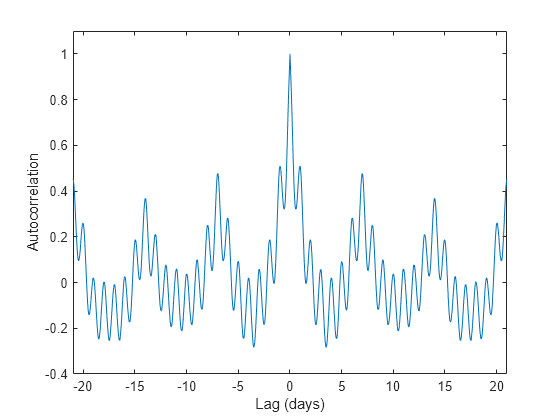
ピークの位置を検出し、これらの間の平均時間差を決定して、短い周期と長い周期を決定します。

長周期を検出するには、短周期より離れていて、高さが 0.3 以上のピークのみを検索するよう findpeaks を制限します。

[pksh,lcsh] = findpeaks(autocor);
short = mean(diff(lcsh))/fs

short = 1.0021

[pklg,lclg] = findpeaks(autocor, ...
    'MinPeakDistance',ceil(short)*fs,'MinPeakheight',0.3);
long = mean(diff(lclg))/fs

long = 6.9896

hold on
pks = plot(lags(lcsh)/fs,pksh,'or', ...
    lags(lclg)/fs,pklg+0.05,'vk');
hold off
legend(pks,[repmat('Period: ',[2 1]) num2str([short;long],0)])
axis([-21 21 -0.4 1.1])

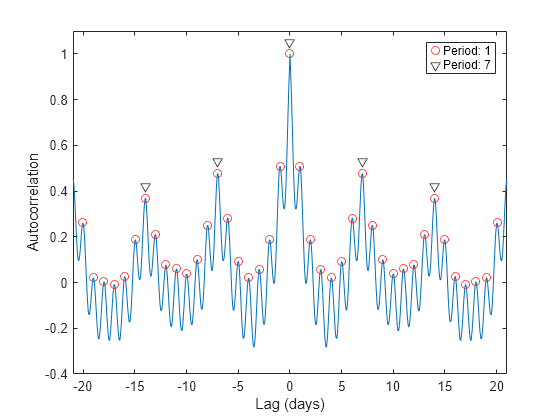
自己相関は、日次でも週次でも、非常によい近似値に収束します。これは予期できることです。ビル内の温度は、人が働いているときは高く、夜間および週末は低くなるためです。

参考

findpeaks | xcorr

関連するトピック

• 周波数解析による周期性の検出