移動平均過程の自己相関
この例では、フィルター処理によってホワイト ノイズ過程に自己相関を発生させる方法を説明します。乱数信号に自己相関を発生させる場合、乱数信号の周波数成分を操作します。移動平均フィルターでは、信号の高周波数成分が減衰されるため、信号は事実上平滑化されます。
3 点移動平均フィルターのインパルス応答を作成します。このフィルターで N(0,1) ホワイト ノイズ列をフィルター処理します。再現性のある結果を得るために、乱数発生器を既定の状態に設定します。
h = 1/3*ones(3,1);
rng default
x = randn(1000,1);
y = filter(h,1,x);サンプルのバイアス付き自己相関を 20 ラグまで求めます。サンプルの自己相関を理論上の自己相関とともにプロットします。
[xc,lags] = xcorr(y,20,'biased'); Xc = zeros(size(xc)); Xc(19:23) = [1 2 3 2 1]/9*var(x); stem(lags,xc,'filled') hold on stem(lags,Xc,'.','linewidth',2) lg = legend('Sample autocorrelation','Theoretical autocorrelation'); lg.Location = 'NorthEast'; lg.Box = 'off';

サンプルの自己相関は、詳細な部分では一致しませんが、理論上の自己相関の一般的な形式を捕らえています。
この場合、フィルターによりラグが [-2,2] の部分にだけ有意な自己相関が生じていることは明白です。シーケンスの絶対値は、この範囲の外側ではすぐにゼロに減衰します。
周波数成分が影響を受けたことを確認するには、元の信号およびフィルター処理後の信号のパワー スペクトル密度のウェルチ推定をプロットします。
[pxx,wx] = pwelch(x); [pyy,wy] = pwelch(y); figure plot(wx/pi,20*log10(pxx),wy/pi,20*log10(pyy)) lg = legend('Original sequence','Filtered sequence'); lg.Location = 'SouthWest'; xlabel('Normalized Frequency (\times\pi rad/sample)') ylabel('Power/frequency (dB/rad/sample)') title('Welch Power Spectral Density Estimate') grid
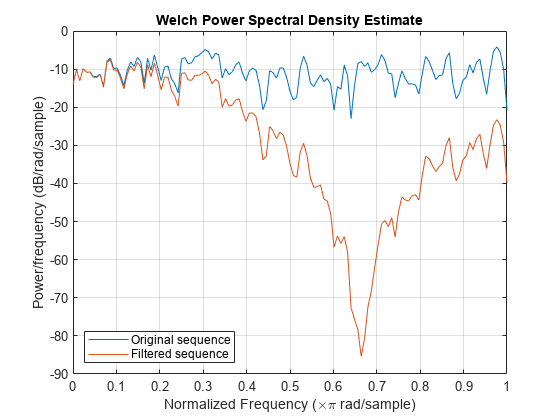
ホワイト ノイズは移動平均フィルターによって "色付け" されています。