Short-dipole Antenna Element
When you want to explicitly study the effects of polarization
in a radar or communication system, you need to specify an antenna
that can generate polarized radiation. One such antenna is the short-dipole
antenna, created by using the phased.ShortDipoleAntennaElement.
The simplest polarized antenna is the dipole antenna which consist of a split length of wire coupled at the middle to a coaxial cable. The simplest dipole, from a mathematical perspective, is the Hertzian dipole, in which the length of wire is much shorter than a wavelength. A diagram of the short dipole antenna of length L appears in the next figure. This antenna is fed by a coaxial feed which splits into two equal length wires of length L/2. The current, I, moves along the z-axis and is assumed to be the same at all points in the wire.

The electric field in the far field has the form
The next example computes the vertical and horizontal polarization components of the field. The vertical component is a function of elevation angle and is axially symmetric. The horizontal component vanishes everywhere.
Short-Dipole Polarization Components
Compute the vertical and horizontal polarization components of the field created by a short-dipole antenna pointed along the z-direction. Plot the components as a function of elevation angle from 0° to 360°.
Create the phased.ShortDipoleAntennaElement System object™.
antenna = phased.ShortDipoleAntennaElement(... 'FrequencyRange',[1,2]*1e9,'AxisDirection','Z');
Compute the antenna response. Because the elevation angle argument to antenna is restricted to ±90°, compute the responses for 0° azimuth and then for 180° azimuth. Combine the two responses in the plot. The operating frequency of the antenna is 1.5 GHz.
el = -90:90; az = zeros(size(el)); fc = 1.5e9; resp = antenna(fc,[az;el]); az = 180.0*ones(size(el)); resp1 = antenna(fc,[az;el]);
Overlay the responses in the same figure.
figure(1) subplot(121) polarplot(el*pi/180.0,abs(resp.V.'),'b') hold on polarplot((el+180)*pi/180.0,abs(resp1.V.'),'b') str = sprintf('%s\n%s','Vertical Polarization','vs Elevation Angle'); title(str) hold off subplot(122) polarplot(el*pi/180.0,abs(resp.H.'),'b') hold on polarplot((el+180)*pi/180.0,abs(resp1.H.'),'b') str = sprintf('%s\n%s','Horizontal Polarization','vs Elevation Angle'); title(str) hold off
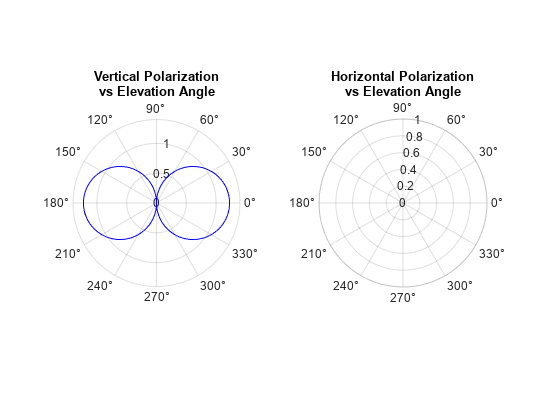
The plot shows that the horizontal component vanishes, as expected.