Antenna Array Analysis with Custom Radiation Pattern
This example shows how to create an antenna array with a custom antenna radiation pattern and then how to analyze the array's response pattern. Such a pattern can be obtained either from measurements or from simulations.
Import the Radiation Pattern
Depending on the application, practical phased antenna arrays sometimes use specially designed antenna elements whose radiation pattern cannot be represented by a closed-form equation. Even when the element pattern is well understood, as is the case with a dipole antenna, the mutual coupling among the elements can significantly change the individual element pattern when the element is put into an array. This makes the closed-form pattern less accurate. Therefore, for high fidelity pattern analysis, you often need to use a custom radiation pattern obtained from measurements or simulations.
There is no standard convention for the coordinate system used to specify the radiation pattern, so the result from one simulation package often cannot not be directly used in another software package. For example, in Phased Array System Toolbox™ (PST), the radiation pattern is expressed using azimuth (az) and elevation (el) angles, as depicted in Figure 1. It is assumed that the main beam of the antenna points toward  azimuth and
azimuth and  elevation, that is, the x-axis. The value of az lies between
elevation, that is, the x-axis. The value of az lies between  and
and  and the value of el lies between
and the value of el lies between  and
and  . See Spherical Coordinates.
. See Spherical Coordinates.

Figure 1: Spherical coordinate system convention used in Phased Array System Toolbox.
A frequently-used full-wave modeling tool for simulating antenna radiation patterns is HFSS™. In this tool, individual elements are modeled as if they were part of an infinite array. The simulated radiation pattern is represented as an M-by-3 matrix where the first column represents the azimuth angle  , the second column represents the elevation angle
, the second column represents the elevation angle  , and the third column represents the radiation pattern in dB. The coordinate system and the definitions of
, and the third column represents the radiation pattern in dB. The coordinate system and the definitions of  and
and  used in HFSS is shown in Figure 2. In this convention, the main beam of the antenna points along the z-axis which usually points vertically. The value of
used in HFSS is shown in Figure 2. In this convention, the main beam of the antenna points along the z-axis which usually points vertically. The value of  is between
is between  and
and  and the value of
and the value of  is between
is between  and
and  .
.

Figure 2: Spherical coordinate system convention used in HFSS.
Note that the HFSS coordinate system is not exactly the same as the  coordinate system used in Phased Array System Toolbox™. In HFSS, the beam mainlobe points along the z-axis and the plane orthogonal to the beam is formed from the x- and y axes. One possible approach to import a custom pattern in
coordinate system used in Phased Array System Toolbox™. In HFSS, the beam mainlobe points along the z-axis and the plane orthogonal to the beam is formed from the x- and y axes. One possible approach to import a custom pattern in  convention without any coordinate axes rotation is shown below.
convention without any coordinate axes rotation is shown below.
For example, a cardioid-shaped antenna pattern is simulated in the  -
-  convention and is saved in a
convention and is saved in a .csv file. The helper function helperPatternImport reads the .csv file and reformats its contents into a two-dimensional matrix in  and
and  .
.
[pattern_phitheta,phi,theta] = helperPatternImport;
The phi-theta pattern can now be used to form a custom antenna element. Assume that this antenna operates between 1 and 1.25 GHz.
freqVector = [1 1.25].*1e9; % Frequency range for element pattern antenna = phased.CustomAntennaElement('FrequencyVector',freqVector, ... 'PatternCoordinateSystem','phi-theta',... 'PhiAngles',phi,... 'ThetaAngles',theta,... 'MagnitudePattern',pattern_phitheta,... 'PhasePattern',zeros(size(pattern_phitheta)));
To verify that the pattern has been correctly imported, plot the response of the custom antenna element. Notice that the main beam points to  azimuth and
azimuth and  elevation, the custom pattern with main beam along z-axis is imported without any rotation.
elevation, the custom pattern with main beam along z-axis is imported without any rotation.
fmax = freqVector(end); pattern(antenna,fmax,'Type','powerdb')

Construct Antenna Array
Consider a 100-element antenna array whose elements reside on a 10-by-10 rectangular grid, as shown in Figure 3. To ensure that no grating lobes appear, elements are spaced at one-half wavelength at the highest operating frequency. This rectangular array can be created using the following commands.

Figure 3: A 10-by-10 URA.
c = physconst('LightSpeed'); lambda = c/fmax; array = phased.URA('Element',antenna,'Size',10,'ElementSpacing',lambda/2)
array =
phased.URA with properties:
Element: [1×1 phased.CustomAntennaElement]
Size: [10 10]
ElementSpacing: [0.1199 0.1199]
Lattice: 'Rectangular'
ArrayNormal: 'x'
Taper: 1
The total radiation pattern of the resulting antenna array is plotted below in u-v space. The pattern is a combination of both the element pattern and the array factor.
pattern(array,fmax,'PropagationSpeed',c,'Type','powerdb',... 'CoordinateSystem','UV');
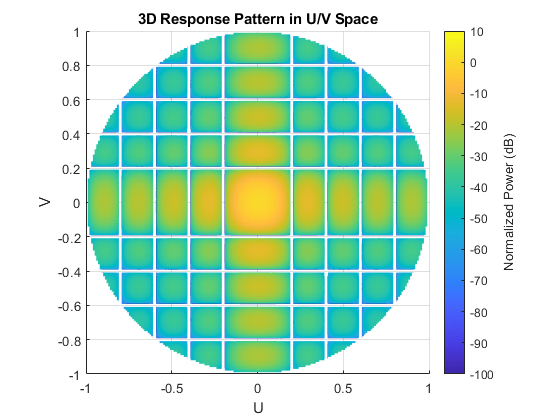
One can also easily examine the u-cut of the pattern as shown below.
pattern(array,fmax,-1:0.01:1,0,'PropagationSpeed',c, ... 'CoordinateSystem','UV','Type','powerdb') axis([-1 1 -50 0]);

Steer the Beam in Azimuth
This section illustrates the idea of phase steering an array. An advantage of phased arrays over a single antenna element is that the main beam can be electronically steered to a given direction. Steering is accomplished by adjusting the weights assigned to each element. The set of weights is also called the steering vector. Each weight is a complex number whose magnitude controls the sidelobe characteristics of the array and whose phase steers the beam.
The example scans the main beam of the array from  azimuth to
azimuth to  azimuth, with the elevation angle fixed at
azimuth, with the elevation angle fixed at  during the scan.
during the scan.
helperPatternScan(array)

clear helperPatternScan
Summary
This example shows how to construct and analyze an antenna array using a custom antenna pattern. The pattern can be generated using full-wave modeling simulation software with the  -
-  convention. The pattern can then be used to form a custom antenna element. The resulting array is scanned from
convention. The pattern can then be used to form a custom antenna element. The resulting array is scanned from  to
to  in the azimuth direction to illustrate the phase steering concept.
in the azimuth direction to illustrate the phase steering concept.