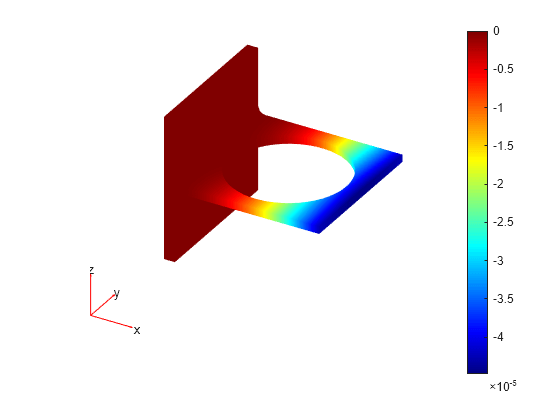StationaryResults

Time-independent PDE solution and derived quantities

Description

A StationaryResults object contains the solution of a PDE and its gradients in a form convenient for plotting and postprocessing.

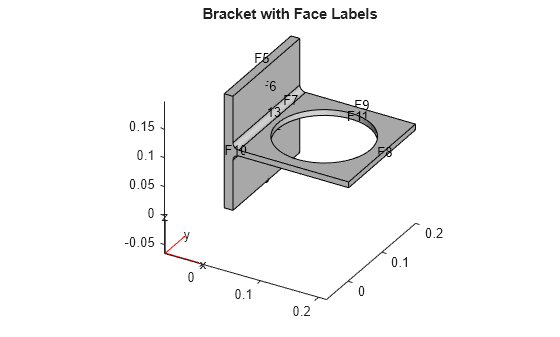
• A StationaryResults object contains the solution and its gradient calculated at the nodes of the triangular or tetrahedral mesh, generated by generateMesh.

• Solution values at the nodes appear in the NodalSolution property.

• The three components of the gradient of the solution values at the nodes appear in the XGradients, YGradients, and ZGradients properties.

• The array dimensions of NodalSolution, XGradients, YGradients, and ZGradients enable you to extract solution and gradient values for specified equation indices in a PDE system.

To interpolate the solution or its gradient to a custom grid (for example, specified by meshgrid), use interpolateSolution or evaluateGradient.

Creation

There are several ways to create a StationaryResults object:

• Solve a time-independent problem using the solvepde function. This function returns a PDE solution as a StationaryResults object. This is the recommended approach.

• Solve a time-independent problem using the assempde or pdenonlin function. Then use the createPDEResults function to obtain a StationaryResults object from a PDE solution returned by assempde or pdenonlin. Note that assempde and pdenonlin are legacy functions. They are not recommended for solving PDE problems.

Properties

Mesh — Finite element mesh

FEMesh object

Finite element mesh, returned as a FEMesh Properties object.

NodalSolution — Solution values at the nodes

vector | array

Solution values at the nodes, returned as a vector or array. For details about the dimensions of NodalSolution, see Dimensions of Solutions, Gradients, and Fluxes.

Data Types: double

XGradients — x-component of gradient at the nodes

vector | array

x-component of the gradient at the nodes, returned as a vector or array. For details about the dimensions of XGradients, see Dimensions of Solutions, Gradients, and Fluxes.

Data Types: double

YGradients — y-component of gradient at the nodes

vector | array

y-component of the gradient at the nodes, returned as a vector or array. For details about the dimensions of YGradients, see Dimensions of Solutions, Gradients, and Fluxes.

Data Types: double

ZGradients — z-component of gradient at the nodes

vector | array

z-component of the gradient at the nodes, returned as a vector or array. For details about the dimensions of ZGradients, see Dimensions of Solutions, Gradients, and Fluxes.

Data Types: double

Object Functions

evaluateCGradient	Evaluate flux of PDE solution
evaluateGradient	Evaluate gradients of PDE solutions at arbitrary points
interpolateSolution	Interpolate PDE solution to arbitrary points

Examples

Obtain a StationaryResults Object from solvepde

Create a PDE model for a system of three equations. Import the geometry of a bracket and plot the face labels.

model = createpde(3);
importGeometry(model,'BracketWithHole.stl');

figure
pdegplot(model,'FaceLabels','on')
view(30,30)
title('Bracket with Face Labels')

figure
pdegplot(model,'FaceLabels','on')
view(-134,-32)
title('Bracket with Face Labels, Rear View')

Set boundary conditions such that face 4 is immobile, and face 8 has a force in the negative z direction.

applyBoundaryCondition(model,'dirichlet','Face',4,'u',[0,0,0]);
applyBoundaryCondition(model,'neumann','Face',8,'g',[0,0,-1e4]);

Set coefficients that represent the equations of linear elasticity. See Linear Elasticity Equations.

E = 200e9;
nu = 0.3;
specifyCoefficients(model,'m',0,...
                          'd',0,...
                          'c',elasticityC3D(E,nu),...
                          'a',0,...
                          'f',[0;0;0]);

Create a mesh.

generateMesh(model,'Hmax',1e-2);

Solve the PDE.

results = solvepde(model)

results = 
  StationaryResults with properties:

    NodalSolution: [14002x3 double]
       XGradients: [14002x3 double]
       YGradients: [14002x3 double]
       ZGradients: [14002x3 double]
             Mesh: [1x1 FEMesh]

Access the solution at the nodal locations.

u = results.NodalSolution;

Plot the solution for the z-component, which is component 3.

pdeplot3D(model,'ColorMapData',u(:,3))

Results from createPDEResults

Obtain a StationaryResults object from a legacy solver together with createPDEResults.

Create a PDE model for a system of three equations. Import the geometry of a bracket and plot the face labels.

model = createpde(3);
importGeometry(model,'BracketWithHole.stl');

figure
pdegplot(model,'FaceLabels','on')
view(30,30)
title('Bracket with Face Labels')

figure
pdegplot(model,'FaceLabels','on')
view(-134,-32)
title('Bracket with Face Labels, Rear View')

Set boundary conditions such that F4 is immobile, and F8 has a force in the negative z direction.

applyBoundaryCondition(model,'dirichlet','Face',4,'u',[0,0,0]);
applyBoundaryCondition(model,'neumann','Face',8,'g',[0,0,-1e4]);

Set coefficients for a legacy solver that represent the equations of linear elasticity. See Linear Elasticity Equations.

E = 200e9;
nu = 0.3;
c = elasticityC3D(E,nu);
a = 0;
f = [0;0;0];

Create a mesh.

generateMesh(model,'Hmax',1e-2);

Solve the problem using a legacy solver.

u = assempde(model,c,a,f);

Create a StationaryResults object from the solution.

results = createPDEResults(model,u)

results = 
  StationaryResults with properties:

    NodalSolution: [14002x3 double]
       XGradients: [14002x3 double]
       YGradients: [14002x3 double]
       ZGradients: [14002x3 double]
             Mesh: [1x1 FEMesh]

Access the solution at the nodal locations.

u = results.NodalSolution;

Plot the solution for the z-component, which is component 3.

pdeplot3D(model,'ColorMapData',u(:,3))