クラスターにおける独立ジョブのベンチマーク
この例では、クラスターで独立ジョブを使用するアプリケーションのベンチマークを実行する方法を示し、ベンチマークの結果を少し詳しく解析します。具体的には、以下のことを行います。
シーケンシャル コードとタスク並列コードの両方が使用されている場合のベンチマークの実行方法を示します。
ストロング スケーリングとウィーク スケーリングについて説明します。
クライアントとクラスターの両方でボトルネックが生じる可能性について検証します。
メモ: この例を大規模なクラスターで実行する場合は 1 時間ほどかかることがあります。
関連する例:
この例のコードは以下の関数に含まれています。
function paralleldemo_distribjob_bench
クラスター プロファイルの確認
クラスターと連携する前に、MATLAB® クライアントがニーズに合わせて構成されていることを確認します。parcluster を呼び出すと、既定のプロファイルを使用するクラスターが返されるか、既定のプロファイルを使用できない場合はエラーがスローされます。
myCluster = parcluster;
時間測定
すべての演算について詳細に調べられるように、演算の実行時間を個別に測定します。どの部分に時間がかかるか把握するため、また、ボトルネックが生じる可能性のある条件を特定するため、それらのすべての詳細な時間測定が必要になります。ここではカード ゲームのブラックジャック (つまり、21) のゲーム数のシミュレーションを実行しますが、この例の目的を考慮すると、どの関数を実際にベンチマーク対象とするかはあまり重要ではありません。
すべての演算は可能な限り効率的なものになるように記述します。たとえば、タスクをベクトル化形式で作成します。すべての演算の経過時間を測定するには、CreateDateTime、StartDateTime、FinishDateTime などのジョブとタスクのプロパティではなく、tic および toc を使用します。これは、tic および toc を使用すると、1 秒未満での精度が得られるためです。また、ベンチマーク計算の実行時間が返されるようにするため、ここではこのタスク関数をインストルメント化しています。
function [times, description] = timeJob(myCluster, numTasks, numHands) % The code that creates the job and its tasks executes sequentially in % the MATLAB client starts here. % We first measure how long it takes to create a job. timingStart = tic; start = tic; job = createJob(myCluster); times.jobCreateTime = toc(start); description.jobCreateTime = 'Job creation time'; % Create all the tasks in one call to createTask, and measure how long % that takes. start = tic; taskArgs = repmat({{numHands, 1}}, numTasks, 1); createTask(job, @pctdemo_task_blackjack, 2, taskArgs); times.taskCreateTime = toc(start); description.taskCreateTime = 'Task creation time'; % Measure how long it takes to submit the job to the cluster. start = tic; submit(job); times.submitTime = toc(start); description.submitTime = 'Job submission time'; % Once the job has been submitted, we hope all its tasks execute in % parallel. We measure how long it takes for all the tasks to start % and to run to completion. start = tic; wait(job); times.jobWaitTime = toc(start); description.jobWaitTime = 'Job wait time'; % Tasks have now completed, so we are again executing sequential code % in the MATLAB client. We measure how long it takes to retrieve all % the job results. start = tic; results = fetchOutputs(job); times.resultsTime = toc(start); description.resultsTime = 'Result retrieval time'; % Verify that the job ran without any errors. if ~isempty([job.Tasks.Error]) taskErrorMsgs = pctdemo_helper_getUniqueErrors(job); delete(job); error('pctexample:distribjobbench:JobErrored', ... ['The following error(s) occurred during task ' ... 'execution:\n\n%s'], taskErrorMsgs); end % Get the execution time of the tasks. Our task function returns this % as its second output argument. times.exeTime = max([results{:,2}]); description.exeTime = 'Task execution time'; % Measure how long it takes to delete the job and all its tasks. start = tic; delete(job); times.deleteTime = toc(start); description.deleteTime = 'Job deletion time'; % Measure the total time elapsed from creating the job up to this % point. times.totalTime = toc(timingStart); description.totalTime = 'Total time'; times.numTasks = numTasks; description.numTasks = 'Number of tasks'; end
以下の測定項目について少し詳しく見てみます。
ジョブ作成時間: ジョブを作成するための時間。MATLAB ジョブ スケジューラ クラスターの場合、これにはリモート呼び出しが必要であり、MATLAB ジョブ スケジューラによってデータベースに領域が割り当てられます。他のタイプのクラスターの場合、ジョブの作成ではいくつかのファイルをディスクに書き込む必要があります。
タスク作成時間: タスク情報を作成して保存するための時間。これは、MATLAB ジョブ スケジューラではデータベースに保存され、他のタイプのクラスターではファイル システム上のファイルに保存されます。
ジョブ投入時間: ジョブを投入するための時間。MATLAB ジョブ スケジューラ クラスターの場合は、データベースに格納されているジョブを開始するように指示します。他のタイプのクラスターの場合は、作成したすべてのタスクを実行するように指示します。
ジョブ待機時間: ジョブの投入から完了までの待機時間。これには、ジョブの投入から完了までの間に実行されるすべてのアクティビティが含まれます。たとえば、クラスターですべてのワーカーを開始してタスク情報をワーカーに送信することが必要になり、ワーカーでタスク情報を読み取ってタスク関数を実行する、といったことです。MATLAB ジョブ スケジューラ クラスターの場合、ワーカーによってタスクの結果が MATLAB ジョブ スケジューラに送信されてデータベースに書き込まれ、他のタイプのクラスターの場合はワーカーによってタスクの結果がディスクに書き込まれます。
タスク実行時間: ブラックジャックのシミュレーションの実行にかかる時間。この時間を正確に測定するためのタスク関数がインストルメント化されています。この時間はジョブ待機時間にも含まれます。
結果取得時間: ジョブの結果を MATLAB クライアントに取り込むための時間。MATLAB ジョブ スケジューラの場合はデータベースから取得します。他のタイプのクラスターの場合はファイル システムから読み取ります。
ジョブ削除時間: すべてのジョブ情報とタスク情報を削除するための時間。MATLAB ジョブ スケジューラの場合はデータベースから削除します。他のタイプのクラスターの場合はファイル システムからそのファイルが削除されます。
合計時間: 上記のすべてを実行するのにかかる時間。
問題の規模の選択
ほとんどのクラスターは中~長時間実行されるジョブをバッチ実行するように設計されています。したがって、ベンチマーク計算はその範囲に収まるように配慮しなければなりません。それだけでなく、この例の実行には何時間もかからないようにしなければならないので、使用するハードウェアで各タスクが 1 分ほどで実行されるように問題の規模を選択します。また、精度を高めるため、時間測定を繰り返し実行します。原則として、タスクでの計算が 1 分よりはるかに短い時間で完了する場合は、レイテンシが短いときのニーズを parfor がジョブおよびタスクより良好に満たすかどうかを検討することをお勧めします。
numHands = 1.2e6; numReps = 5;
ここでは、さまざまな数 (1、2、4、8、16 個から始まり、使用できる上限数まで) のワーカーで高速化を実行してみます。この例では、ベンチマークでクラスターへの専用アクセスを使用することと、クラスターの NumWorkers プロパティが正しく設定されていることを前提としています。その場合、各タスクは専用ワーカーで即座に実行されるので、投入されるタスクの数とそれらのタスクを実行するワーカーの数が同じになります。
numWorkers = myCluster.NumWorkers ; if isinf(numWorkers) || (numWorkers == 0) error('pctexample:distribjobbench:InvalidNumWorkers', ... ['Cannot deduce the number of workers from the cluster. ' ... 'Set the NumWorkers on your default profile to be ' ... 'a value other than 0 or inf.']); end numTasks = [pow2(0:ceil(log2(numWorkers) - 1)), numWorkers];
ウィーク スケーリングによる測定
ここでは、ジョブに含まれているタスクの数を変更し、各タスクで一定量の処理が実行されるようにします。この方法はウィーク スケーリングと呼ばれるものです。通常、比較的大きな規模の問題を解くためにはクラスターをスケールアップするので、最も注目すべき方法です。この例で後述するストロング スケーリングとこれを比較してみてください。ウィーク スケーリングに基づく高速化はスケーリングされた高速化とも呼ばれます。
fprintf(['Starting weak scaling timing. ' ... 'Submitting a total of %d jobs.\n'], numReps*length(numTasks)); for j = 1:length(numTasks) n = numTasks(j); for itr = 1:numReps [rep(itr), description] = timeJob(myCluster, n, numHands); %#ok<AGROW> end % Retain the iteration with the lowest total time. totalTime = [rep.totalTime]; fastest = find(totalTime == min(totalTime), 1); weak(j) = rep(fastest); %#ok<AGROW> fprintf('Job wait time with %d task(s): %f seconds\n', ... n, weak(j).jobWaitTime); end
Starting weak scaling timing. Submitting a total of 45 jobs. Job wait time with 1 task(s): 59.631733 seconds Job wait time with 2 task(s): 60.717059 seconds Job wait time with 4 task(s): 61.343568 seconds Job wait time with 8 task(s): 60.759119 seconds Job wait time with 16 task(s): 63.016560 seconds Job wait time with 32 task(s): 64.615484 seconds Job wait time with 64 task(s): 66.581806 seconds Job wait time with 128 task(s): 91.043285 seconds Job wait time with 256 task(s): 150.411704 seconds
逐次実行
ここでは、計算の逐次実行時間を測定します。ただし、この時間は、複数のクラスターが同じハードウェア構成とソフトウェア構成を使用している場合にのみ、それらのクラスター間で比較されます。
seqTime = inf; for itr = 1:numReps start = tic; pctdemo_task_blackjack(numHands, 1); seqTime = min(seqTime, toc(start)); end fprintf('Sequential execution time: %f seconds\n', seqTime);
Sequential execution time: 84.771630 seconds
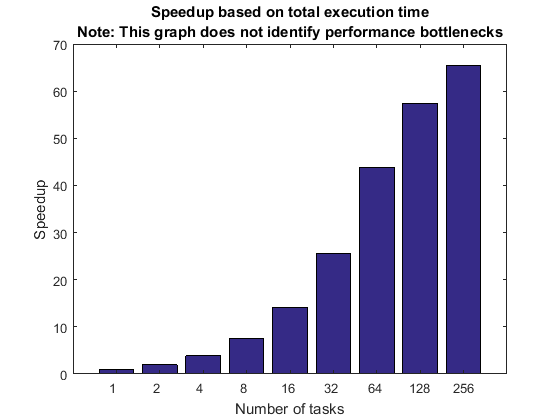
ウィーク スケーリングと合計実行時間に基づく高速化
最初に、さまざまな数のワーカーで実現される全体的な高速化について考えます。高速化は計算にかかる合計時間に基づいて実現されるので、コードの逐次実行部分と並列実行部分の両方が関連します。
この高速化曲線は、それぞれに関連付けられている重みが不明である次のような複数の項目の性能を表します。クラスター ハードウェア、クラスター ソフトウェア、クライアント ハードウェア、クライアント ソフトウェアおよびクライアントとクラスターの間の接続です。つまり、高速化曲線は、それらのいずれか 1 つではなく、すべてまとめたものを表すということです。
高速化曲線がパフォーマンス目標を満たす場合は、この特定のベンチマークに関しては前述のすべての要素がうまく連携していることになります。一方、高速化曲線が目標を満たしていない場合は、前述のどの要素が最大の要因であるかはわかりません。場合によっては、一方のソフトウェアやハードウェアのいずれかではなく、アプリケーションの並列化の手法自体が原因である可能性もあります。
初心者ユーザーは、このたった 1 つのグラフからクラスターのハードウェアやソフトウェアのパフォーマンスの全体像を把握できると思い込むことがよくあります。しかし、そのようなことは決してないので、パフォーマンスでボトルネックが生じる可能性に関して、このグラフからはいかなる結論も導き出してはならないことを常に認識しておく必要があります。
titleStr = sprintf(['Speedup based on total execution time\n' ... 'Note: This graph does not identify performance ' ... 'bottlenecks']); pctdemo_plot_distribjob('speedup', [weak.numTasks], [weak.totalTime], ... weak(1).totalTime, titleStr);
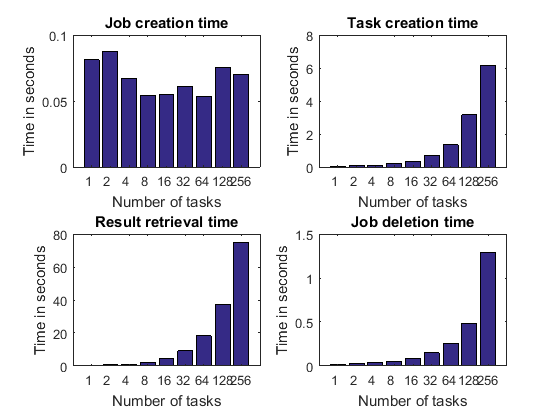
詳細なグラフ - パート 1
ここでは、コードのさまざまなステップの所要時間について、もう少し詳しく見てみます。直前の例では、ウィーク スケーリングによるベンチマークを実行しました。ウィーク スケーリングでは、作成するタスクの数に比例して実行される処理を増加させます。したがって、タスク出力データのサイズはタスクの数が増加するにつれて大きくなります。その点を考慮すると、作成するタスクの数が増加するにつれて、以下の処理にかかる時間が長くなるものと予測されます。
タスク作成
ジョブ出力引数の取得
ジョブの破棄にかかる時間
以下に示す時間は、タスクの数が増加しても長くなるとは考えられません。
ジョブ作成時間
いずれにせよ、ジョブはそれ自体のタスクが定義される前に作成されるので、ジョブ作成時間がタスクの数に伴って変化する理由はありません。ジョブ作成時間については、ランダムにほんのわずか変動するだけと考えられます。
pctdemo_plot_distribjob('fields', weak, description, ... {'jobCreateTime', 'taskCreateTime', 'resultsTime', 'deleteTime'}, ... 'Time in seconds');
正規化された時間
タスク作成時間はタスク数が増加するにつれて長くなり、ジョブ出力引数の取得時間およびジョブ削除時間についても同様であるということは既に確認しました。ただし、そのようになるのは、ワーカーまたはタスクの数が増加するにつれて、実行される処理の量も増加するという事実に基づくためです。したがって、以下の 3 つのアクティビティについて該当の演算を実行するのにかかる時間を確認してそれぞれの効率性を測定し、タスク数によって正規化することは有効であると言えます。このようにすると、以下に示す時間がタスク数の変化に対してそれぞれ一定に維持されるか、増加または減少するかということを確認できます。
単一のタスクの作成にかかる時間
単一のタスクから出力引数を取得するためにかかる時間
ジョブのタスクの 1 つを削除するためにかかる時間
以下のグラフに示されている正規化された時間は、MATLAB クライアントの性能および MATLAB クライアントがデータをやり取りするクラスターのハードウェア部分またはソフトウェア部分の性能を表しています。一般的に、変動がない場合は性能が良好であり、減少傾向を示す場合は優れていると考えられます。
pctdemo_plot_distribjob('normalizedFields', weak, description, ... {'taskCreateTime', 'resultsTime', 'deleteTime'});
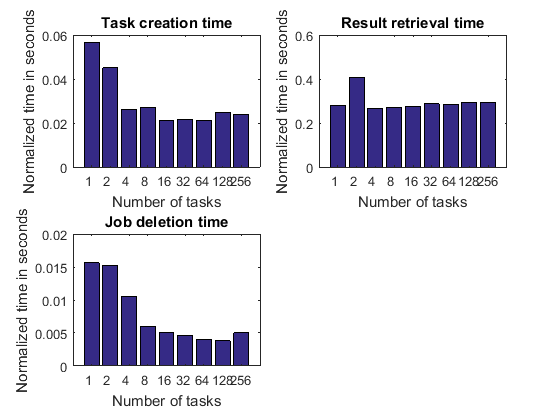
これらのグラフから、タスク数が増加するにつれてタスクごとの結果の取得時間が短くなっていることがわかる場合があります。これはまさに歓迎すべきことです。実行される処理の量が増加するにつれて効率性が向上しているためです。このような状況は演算のオーバーヘッドが一定であり、ジョブのタスクごとの実行時間が一定である場合に見られることがあります。
上記のような逐次実行のアクティビティに大幅な時間がかかり、タスク数が増加するにつれて実行時間が長くなる場合は、合計実行時間に基づく高速化曲線ではあまり良い結果は得られません。その場合、タスク数が極めて多くなると、逐次実行のアクティビティに大半の時間が費やされることになります。
詳細なグラフ - パート 2
以下のそれぞれのステップに必要な時間はタスク数に応じて変動する可能性がありますが、そのようなことは望ましいものではありません。
ジョブ投入時間
タスク実行時間。ここではブラックジャックのシミュレーションにかかる時間を表します。それ以外の処理は含まれません。
いずれの場合も、経過時間 (クロック時間) を確認します。クラスターの総 CPU 時間でも正規化された時間でもありません。
pctdemo_plot_distribjob('fields', weak, description, ... {'submitTime', 'exeTime'});
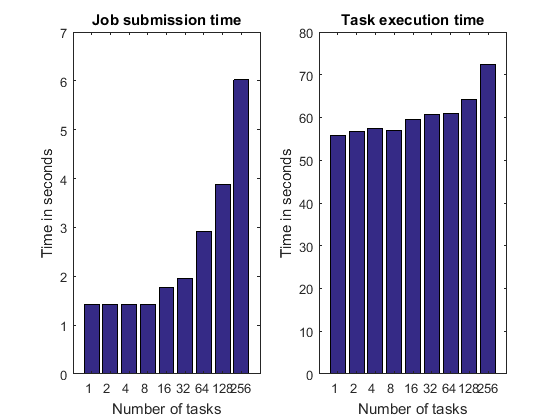
上記のそれぞれの時間はタスク数に応じて長くなることがあります。以下に例を示します。
サードパーティのクラスター タイプによっては、ジョブ投入でジョブのタスクごとに 1 回ずつシステム呼び出しを実行することやネットワーク経由でファイルをコピーすることが必要な場合があります。このような場合、ジョブ投入時間がタスク数に比例して長くなる可能性があります。
タスク実行時間のグラフにはハードウェアに関する制限とリソース競合の影響が最も顕著に表れるものと考えられます。たとえば、複数のワーカーを同じコンピューターで実行する場合は、メモリ帯域幅が限られるために競合が発生してタスク実行時間が長くなることがあります。リソース競合のその他の例として、タスク関数で単一の共有ファイル システムを使用して大きなデータを読み取ったり書き込んだりする場合が挙げられます。ただし、この例のタスク関数ではファイル システムには一切アクセスしません。このようなタイプのハードウェア制限については、タスク並列処理におけるリソース競合の問題の例で詳しく説明しています。
ウィーク スケーリングとジョブ待機時間に基づく高速化
コードのさまざまな段階で費やされる時間についての検討が済んだので、ここでは、クラスターのハードウェアとソフトウェアの性能をより正確に表す高速化曲線を作成してみます。そのための方法として、ジョブ待機時間に基づいて高速化曲線を導き出します。
ジョブ待機時間に基づいて高速化曲線を作成するにあたり、最初に、単一のタスクから構成されるジョブをクラスターで実行するのに必要な時間とジョブ待機時間を比較します。
titleStr = 'Speedup based on job wait time compared to one task'; pctdemo_plot_distribjob('speedup', [weak.numTasks], [weak.jobWaitTime], ... weak(1).jobWaitTime, titleStr);

ジョブ待機時間にはすべての MATLAB ワーカーを開始するための時間が含まれることがあります。したがって、この時間は共有ファイル システムの IO 性能によって制限される可能性があります。ジョブ待機時間には平均タスク実行時間も含まれるので、平均タスク実行時間に関する問題も反映されます。クラスターへの専用アクセスがない場合は、ジョブ待機時間に基づく高速化曲線に著しく影響するものと考えられます。
次に、クライアント コンピューターのハードウェアが計算ノードのハードウェアと同程度のものであることを前提として、ジョブ待機時間を逐次実行時間と比較します。クライアントがクラスター ノードと同程度のものでない場合は、この比較を行っても意味がありません。タスクをワーカーに割り当てるとき (たとえば、1 分間に 1 回だけタスクをワーカーに割り当てる場合など) にクラスターで大幅なタイム ラグが発生する場合は、このグラフには著しい影響があります。これは、逐次実行時間については、そのようなタイム ラグが原因で長くなることはないためです。このグラフは既出のグラフと同じ形になり、乗法係数が一定であるという点のみが異なるということに注目してください。
titleStr = 'Speedup based on job wait time compared to sequential time'; pctdemo_plot_distribjob('speedup', [weak.numTasks], [weak.jobWaitTime], ... seqTime, titleStr);
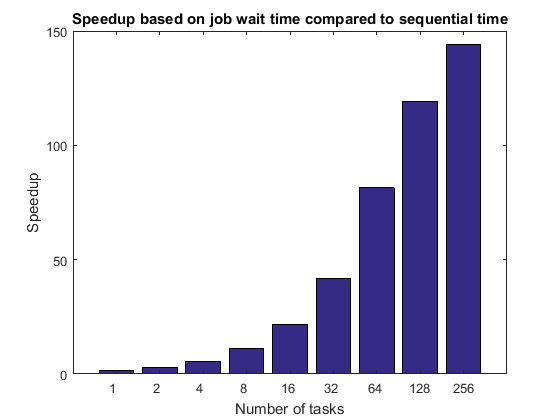
ジョブ待機時間とタスク実行時間の比較
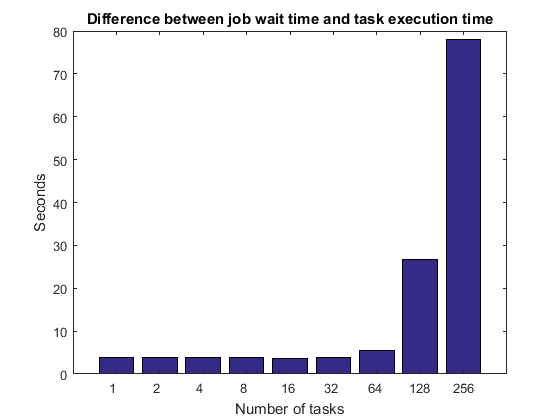
既に説明したようにジョブ待機時間は、スケジューリング、クラスターのキューでの待機時間、MATLAB の起動時間などをタスク実行時間に加えたものです。アイドル状態のクラスターから始めると、少なくともタスク数が限られたものである場合は、ジョブ待機時間とタスク実行時間の差は一定に維持されます。タスク数が数十、数百、数千へと増加するにつれて、最終的には何らかの制限に直面することになります。たとえば、タスクまたはワーカーの数が極めて多くなると、クラスターですべてのワーカーに対してタスクの実行開始を同時に指示できなくなります。あるいは、すべての MATLAB ワーカーで同じファイル システムを使用する場合には、ファイル サーバーが飽和状態になる可能性があります。
titleStr = 'Difference between job wait time and task execution time'; pctdemo_plot_distribjob('barTime', [weak.numTasks], ... [weak.jobWaitTime] - [weak.exeTime], titleStr);
ストロング スケーリングによる測定
ここでは、問題を解くために使用するワーカー数を変更し、問題のサイズは固定した場合の実行時間を測定します。これはストロング スケーリングと呼ばれるものです。ただし、アプリケーションに何らかの逐次実行部分がある場合は、ストロング スケーリングによって実現できる高速化には限界があるということがよく言われています。そのことは、アムダールの法則で公式化されており、長年にわたって広く議論されています。
クラスターにジョブを投入する場合、ストロング スケーリングによる高速化の限界に直面することは珍しいことではありません。タスク実行のオーバーヘッドが変動しない場合 (そのようなことはよくあります)、たとえそのオーバーヘッドがわずか 1 秒であっても、アプリケーションでのこのタスク実行時間が 1 秒を下回るようになることは決してありません。ここではまず、1 つの MATLAB ワーカーの場合に約 60 秒間で実行されるアプリケーションについて考えます。計算を 60 個のワーカーで分割すれば、それぞれのワーカーが問題全体のうちの担当部分を完了するのにわずか 1 秒しかかかりません。ただし、そのように仮定した場合、1 秒というタスク実行オーバーヘッドは全体的な実行時間を左右する重要な要素となります。
アプリケーションの実行時間が長いものではない限り、通常、ジョブおよびタスクを使用しても、ストロング スケーリングで優れた成果をあげることはできません。タスク実行のオーバーヘッドがアプリケーションの実行時間に近い場合は、parfor を使用することで要件を満たせるかどうかを検討することを推奨します。parfor の場合でも、オーバーヘッドは通常のジョブおよびタスクの場合に比べればかなり小さいものの一定量が発生し、ストロング スケーリングで実現できる高速化が制限されます。クラスター サイズに応じて設定される問題の規模の大きさによって、それらの制限が発生することも、発生しないこともあります。
原則的に、多数のプロセッサで小さな問題のストロング スケーリングを実現するには、専用ハードウェアと多くのプログラミング作業が必要になります。
fprintf(['Starting strong scaling timing. ' ... 'Submitting a total of %d jobs.\n'], numReps*length(numTasks)) for j = 1:length(numTasks) n = numTasks(j); strongNumHands = ceil(numHands/n); for itr = 1:numReps rep(itr) = timeJob(myCluster, n, strongNumHands); end ind = find([rep.totalTime] == min([rep.totalTime]), 1); strong(n) = rep(ind); %#ok<AGROW> fprintf('Job wait time with %d task(s): %f seconds\n', ... n, strong(n).jobWaitTime); end
Starting strong scaling timing. Submitting a total of 45 jobs. Job wait time with 1 task(s): 60.531446 seconds Job wait time with 2 task(s): 31.745135 seconds Job wait time with 4 task(s): 18.367432 seconds Job wait time with 8 task(s): 11.172390 seconds Job wait time with 16 task(s): 8.155608 seconds Job wait time with 32 task(s): 6.298422 seconds Job wait time with 64 task(s): 5.253394 seconds Job wait time with 128 task(s): 5.302715 seconds Job wait time with 256 task(s): 49.428909 seconds
ストロング スケーリングと合計実行時間に基づく高速化
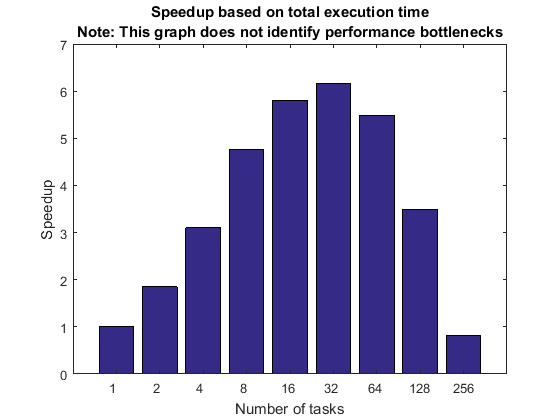
既に説明したように、MATLAB クライアントにおけるシーケンシャル コードの実行時間の合計とクラスターにおける並列コードの実行時間を表す高速化曲線は誤解を招きやすいものです。以下のグラフは、ストロング スケーリングによるシナリオで最悪のケースが発生した場合のこれらの情報を示しています。クラスター サイズに対して問題の規模が非常に小さくなるような元の問題を意図的に選び、悪い例となるような高速化曲線が作成されるようにします。クラスターのハードウェアもソフトウェアもこの種の用途を考慮して設計されてはいません。
titleStr = sprintf(['Speedup based on total execution time\n' ... 'Note: This graph does not identify performance ' ... 'bottlenecks']); pctdemo_plot_distribjob('speedup', [strong.numTasks], ... [strong.totalTime].*[strong.numTasks], strong(1).totalTime, titleStr);
タスク実行時間の短縮化の代替方法: parfor
意図的にジョブおよびタスクにおける計算の実行時間が短くなるようにしたので、ストロング スケーリングの結果は良好なものにはなりませんでした。ここでは、同じ問題に parfor を適用する方法を示します。プールを開くためにかかる時間は測定時間には含めないことに注意してください。
pool = parpool(numWorkers); parforTime = inf; strongNumHands = ceil(numHands/numWorkers); for itr = 1:numReps start = tic; r = cell(1, numWorkers); parfor i = 1:numWorkers r{i} = pctdemo_task_blackjack(strongNumHands, 1); %#ok<PFOUS> end parforTime = min(parforTime, toc(start)); end delete(pool);
Starting parallel pool (parpool) using the 'bigMJS' profile ... connected to 256 workers. Analyzing and transferring files to the workers ...done.
parfor によるストロング スケーリングに基づく高速化
元の逐次計算の実行時間が 1 分程度なので、大規模なクラスターで各ワーカーが計算を実行するのに必要な時間はわずか数秒です。したがって、ストロング スケーリングによるパフォーマンスは parfor の場合の方がジョブおよびタスクの場合よりもはるかに高いと予測されます。
fprintf('Execution time with parfor using %d workers: %f seconds\n', ... numWorkers, parforTime); fprintf(['Speedup based on strong scaling with parfor using ', ... '%d workers: %f\n'], numWorkers, seqTime/parforTime);
Execution time with parfor using 256 workers: 1.126914 seconds Speedup based on strong scaling with parfor using 256 workers: 75.224557
概要
これまで、ウィーク スケーリングとストロング スケーリングの違いを確認し、なぜウィーク スケーリングの方が望ましいのかということについて説明しました。クラスターでより大きな問題を解く (より多くのシミュレーション、反復、データなどを実行する) ための性能を測定しました。また、この例に記載した多数のグラフおよび詳細情報から、ベンチマークは 1 つの数値または 1 つのグラフに集約できるものではないということも明らかになりました。アプリケーションのパフォーマンスがアプリケーション、クラスターのハードウェアまたはソフトウェア、それらの両方の組み合わせのいずれによって決まるかを把握するには全体像に目を向ける必要があります。
また、簡単な計算では parfor がジョブおよびタスクよりも優れた代替方法となり得ることも確認しました。parfor を使用するベンチマークの他の結果については、ブラックジャックを使用した parfor のシンプルなベンチマークの例を参照してください。
end