ポートフォリオ最適化問題に対する二次計画法、ソルバーベース
この例では、quadprog の内点二次計画法アルゴリズムを使用して、ポートフォリオ最適化の問題を解く方法を示します。関数 quadprog は、Optimization Toolbox™ に含まれています。
この例の問題を定義する行列は高密度ですが、quadprog の内点法アルゴリズムでは、問題の行列にあるスパースを活用して速度を上げることもできます。スパースの例については、内点法アルゴリズムを使った大規模なスパース二次計画法を参照してください。
二次モデル
 種類の資産があるとします。資産
種類の資産があるとします。資産  の収益率は、期待値が
の収益率は、期待値が 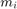 の確率変数です。問題は、指定された最小期待収益率を条件として、リスクを最小限にするには、どの割合
の確率変数です。問題は、指定された最小期待収益率を条件として、リスクを最小限にするには、どの割合 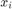 で各資産
で各資産  に投資するかを求めることです。
に投資するかを求めることです。
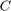 は資産収益率の共分散行列を示すとします。
は資産収益率の共分散行列を示すとします。
従来の平均分散モデルは、以下の測定でポートフォリオ リスクを最小化し、
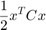
これは一連の制約に従います。
期待される収益は、投資家が望むポートフォリオの最小期待収益率  を下回ってはなりません。
を下回ってはなりません。
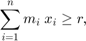
投資割合 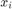 の合計は 1 にならなければなりません。
の合計は 1 にならなければなりません。
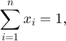
そして、割合 (またはパーセント) は、0 と 1 の間の数でなければなりません。
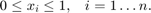
ポートフォリオ リスクを最小限に抑えるという目的関数は二次で制約は線形であるため、最適化問題は最終的に二次計画、つまり QP となります。
225 資産問題
ここで、225 資産をもつ QP を解いてみます。データセットは、OR ライブラリ [Chang, T.-J., Meade, N., Beasley, J.E. and Sharaiha, Y.M., "Heuristics for cardinality constrained portfolio optimisation" Computers & Operations Research 27 (2000) 1271-1302] からの引用です。
データセットを読み込み、制約を quadprog で期待する形式に設定します。このデータセットでは、収益率 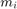 は -0.008489 ~ 0.003971 の範囲にあります。その中から望ましい収益
は -0.008489 ~ 0.003971 の範囲にあります。その中から望ましい収益  、たとえば 0.002 (0.2%) を選択します。
、たとえば 0.002 (0.2%) を選択します。
MAT ファイルに保存されているデータセットを読み込みます。
load('port5.mat','Correlation','stdDev_return','mean_return')
共分散行列を相関行列から計算します。
Covariance = Correlation .* (stdDev_return * stdDev_return'); nAssets = numel(mean_return); r = 0.002; % number of assets and desired return Aeq = ones(1,nAssets); beq = 1; % equality Aeq*x = beq Aineq = -mean_return'; bineq = -r; % inequality Aineq*x <= bineq lb = zeros(nAssets,1); ub = ones(nAssets,1); % bounds lb <= x <= ub c = zeros(nAssets,1); % objective has no linear term; set it to zero
quadprog の内点法アルゴリズムの選択
内点法アルゴリズムを使用して QP を解くには、オプションのアルゴリズムを「内点法凸」に設定します。
options = optimoptions('quadprog','Algorithm','interior-point-convex');
225 資産問題の解法
ここでは、いくつかの追加オプションを設定し、ソルバー quadprog を呼び出します。
追加オプションを設定します。反復表示をオンにして、最適性に関する終了許容誤差を小さくします。
options = optimoptions(options,'Display','iter','TolFun',1e-10);
ソルバーを呼び出し、時計時間を測定します。
tic [x1,fval1] = quadprog(Covariance,c,Aineq,bineq,Aeq,beq,lb,ub,[],options); toc
Iter Fval Primal Infeas Dual Infeas Complementarity
0 2.384401e+01 2.253410e+02 1.337381e+00 1.000000e+00
1 1.338822e-03 7.394864e-01 4.388791e-03 1.038098e-02
2 1.186079e-03 6.443975e-01 3.824446e-03 8.727381e-03
3 5.923977e-04 2.730703e-01 1.620650e-03 1.174211e-02
4 5.354880e-04 5.303581e-02 3.147632e-04 1.549549e-02
5 5.181994e-04 2.651791e-05 1.573816e-07 2.848171e-04
6 5.066191e-04 9.285375e-06 5.510794e-08 1.041224e-04
7 3.923090e-04 7.619855e-06 4.522322e-08 5.536006e-04
8 3.791545e-04 1.770065e-06 1.050519e-08 1.382075e-04
9 2.923749e-04 8.850307e-10 5.252593e-12 3.858983e-05
10 2.277722e-04 4.422812e-13 2.626936e-15 6.204101e-06
11 1.992243e-04 4.336809e-19 1.387779e-17 4.391483e-07
12 1.950468e-04 2.229120e-16 9.592302e-19 1.429441e-08
13 1.949141e-04 0.000000e+00 9.611235e-19 9.731942e-10
14 1.949121e-04 6.670012e-16 6.938894e-18 2.209702e-12
Minimum found that satisfies the constraints.
Optimization completed because the objective function is non-decreasing in
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.
Elapsed time is 0.177013 seconds.
結果をプロットします。
plotPortfDemoStandardModel(x1)
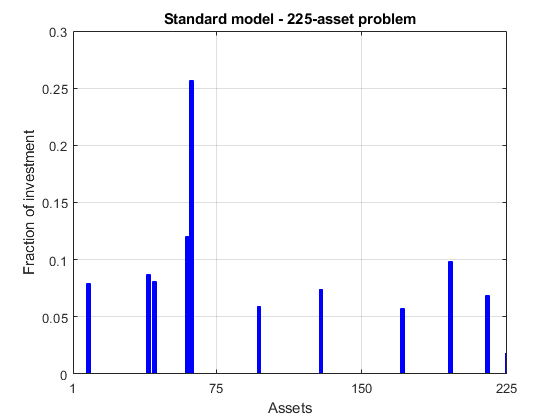
グループ制約付き 225 資産問題
資産 1 ~ 75、76 ~ 150、151 ~ 225 のそれぞれに投資金額の 30% を投資することを要求する制約をモデル グループに追加します。これらの資産グループのそれぞれは、たとえば技術、自動車、医薬品など産業が異なることもあります。この新しい要件を含む制約は、以下のとおりです。
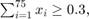
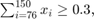
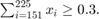
既存の等式にグループ制約を追加します。
Groups = blkdiag(ones(1,nAssets/3),ones(1,nAssets/3),ones(1,nAssets/3)); Aineq = [Aineq; -Groups]; % convert to <= constraint bineq = [bineq; -0.3*ones(3,1)]; % by changing signs
ソルバーを呼び出し、時計時間を測定します。
tic [x2,fval2] = quadprog(Covariance,c,Aineq,bineq,Aeq,beq,lb,ub,[],options); toc
Iter Fval Primal Infeas Dual Infeas Complementarity
0 2.384401e+01 4.464410e+02 1.337324e+00 1.000000e+00
1 1.346872e-03 1.474737e+00 4.417606e-03 3.414918e-02
2 1.190113e-03 1.280566e+00 3.835962e-03 2.934585e-02
3 5.990845e-04 5.560762e-01 1.665738e-03 1.320038e-02
4 3.890097e-04 2.780381e-04 8.328691e-07 7.287370e-03
5 3.887354e-04 1.480950e-06 4.436214e-09 4.641988e-05
6 3.387787e-04 8.425389e-07 2.523842e-09 2.578178e-05
7 3.089240e-04 2.707587e-07 8.110631e-10 9.217509e-06
8 2.639458e-04 6.586817e-08 1.973094e-10 6.509001e-06
9 2.252657e-04 2.225507e-08 6.666550e-11 6.783212e-06
10 2.105838e-04 5.811528e-09 1.740855e-11 1.967570e-06
11 2.024362e-04 4.130058e-12 1.237032e-14 5.924109e-08
12 2.009704e-04 4.840746e-15 1.404304e-17 6.354389e-10
13 2.009650e-04 1.499235e-15 6.938894e-18 1.889136e-13
Minimum found that satisfies the constraints.
Optimization completed because the objective function is non-decreasing in
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.
Elapsed time is 0.064789 seconds.
結果を前の問題の結果に重ね合わせてプロットします。
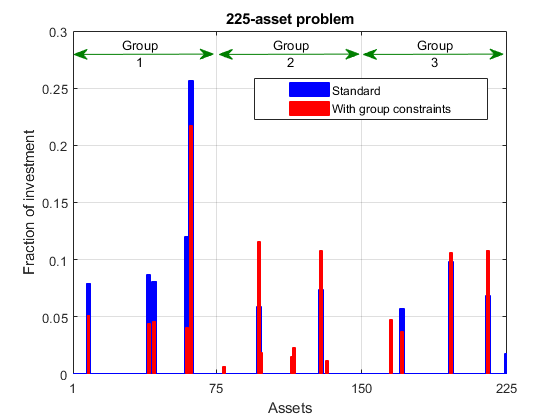
plotPortfDemoGroupModel(x1,x2);
これまでの結果の概要
2 番目の棒グラフを見ると、このポートフォリオは、グループ制約を追加したことにより、最初のポートフォリオと比べて 3 つの資産グループへの分配がより均一であることがわかります。また、この多様性により、目的関数 (両実行の反復表示で最後の反復に "f(x)" が付いている列を参照) で測定したところ、リスクがわずかに増加する結果となりました。
乱数データを使用した 1000 資産問題
quadprog の内点法アルゴリズムがより大きな問題でどのような動作を行うかを示すため、1000 資産のランダムに生成されたデータセットを使用します。MATLAB® で関数 gallery を使用して、ランダム相関行列 (対称、半正定値、対角要素が 1) を生成します。
再現性が必要な場合は、乱数ストリームをリセットします。
rng(0,'twister'); nAssets = 1000; % desired number of assets
-0.1 ~ 0.4 の収益の平均を生成します。
a = -0.1; b = 0.4; mean_return = a + (b-a).*rand(nAssets,1);
0.08 ~ 0.6 の収益の標準偏差を生成します。
a = 0.08; b = 0.6; stdDev_return = a + (b-a).*rand(nAssets,1); % Correlation matrix, generated using Correlation = gallery('randcorr',nAssets). % (Generating a correlation matrix of this size takes a while, so we load % a pre-generated one instead.) load('correlationMatrixDemo.mat','Correlation'); % Calculate covariance matrix from correlation matrix. Covariance = Correlation .* (stdDev_return * stdDev_return');
ランダムに作成された 1000 資産問題の定義と解法
それでは、標準的な QP 問題 (ここではグループ制約なし) を定義し、解いてみます。
r = 0.15; % desired return Aeq = ones(1,nAssets); beq = 1; % equality Aeq*x = beq Aineq = -mean_return'; bineq = -r; % inequality Aineq*x <= bineq lb = zeros(nAssets,1); ub = ones(nAssets,1); % bounds lb <= x <= ub c = zeros(nAssets,1); % objective has no linear term; set it to zero
ソルバーを呼び出し、時計時間を測定します。
tic x3 = quadprog(Covariance,c,Aineq,bineq,Aeq,beq,lb,ub,[],options); toc
Iter Fval Primal Infeas Dual Infeas Complementarity
0 7.083800e+01 1.142266e+03 1.610094e+00 1.000000e+00
1 5.603619e-03 7.133717e+00 1.005541e-02 9.857295e-02
2 1.076070e-04 3.566858e-03 5.027704e-06 9.761758e-03
3 1.068230e-04 2.513041e-06 3.542285e-09 8.148386e-06
4 7.257177e-05 1.230928e-06 1.735068e-09 3.979480e-06
5 3.610589e-05 2.634706e-07 3.713780e-10 1.175001e-06
6 2.077811e-05 2.562892e-08 3.612554e-11 5.617206e-07
7 1.611590e-05 4.711777e-10 6.641535e-13 5.652911e-08
8 1.491953e-05 4.923423e-12 6.940538e-15 2.427880e-09
9 1.477930e-05 1.317002e-13 1.850938e-16 2.454705e-10
10 1.476910e-05 3.608225e-16 8.408650e-19 2.786060e-11
Minimum found that satisfies the constraints.
Optimization completed because the objective function is non-decreasing in
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.
Elapsed time is 0.765688 seconds.
まとめ
この例では、ポートフォリオ最適化問題において quadprog の内点法アルゴリズムを使用する方法を説明し、さまざまなサイズの二次問題におけるアルゴリズム実行時間を示します。
特に Financial Toolbox™ でのポートフォリオ最適化用に設計された機能を使用すると、より詳細な分析が可能です。