内点法アルゴリズムを使った大規模なスパース二次計画法
この例は、スパース問題を解くときにスパース演算を使用することの価値を示しています。行列は n 行です。大きい値の n と、いくつかの非ゼロの対角帯を選択します。n 行 n 列の完全な行列は使用可能なメモリをすべて使用することがありますが、スパース行列は問題を起こしません。
問題は以下の制約に従って x'*H*x/2 + f'*x を最小化することです。
x(1) + x(2) + ... + x(n) <= 0,
ここで、f = [-1;-2;-3;...;-n]、H はスパース対称帯行列です。
スパース二次行列の作成
ベクトル [3,6,2,14,2,6,3] の、14 を主対角に置いたシフトにより、対称循環行列を作成します。行列は n 行 n 列にします。ここで、n = 30,000 です。
n = 3e4;
H2 = speye(n);
H = 3*circshift(H2,-3,2) + 6*circshift(H2,-2,2) + 2*circshift(H2,-1,2)...
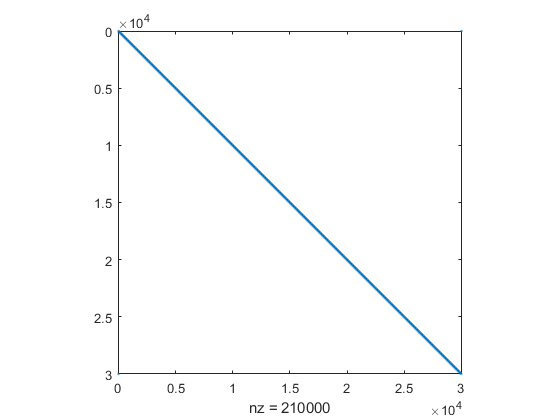
+ 14*H2 + 2*circshift(H2,1,2) + 6*circshift(H2,2,2) + 3*circshift(H2,3,2);行列構造を表示します。
spy(H)
線形制約と目的関数の作成
線形制約は、解の要素の合計が非正であるというものです。目的関数には、ベクトル f で表現された線形項が含まれます。
A = ones(1,n); b = 0; f = 1:n; f = -f;
問題を解く
interior-point-convex' アルゴリズムを使用して二次計画問題を解きます。ソルバーが途中で停止しないように、StepTolerance オプションを 0 に設定します。
options = optimoptions(@quadprog,'Algorithm','interior-point-convex','StepTolerance',0); [x,fval,exitflag,output,lambda] = ... quadprog(H,f,A,b,[],[],[],[],[],options);
Minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the value of the optimality tolerance, and constraints are satisfied to within the value of the constraint tolerance. <stopping criteria details>
n = 30,000 の場合、多くのコンピューターでは、完全な n 行 n 列の行列を作成することができません。したがって、この問題はスパース行列を使用してのみ実行できます。
解の検証
目的関数の値と反復回数を表示し、線形不等式に関連付けられたラグランジュ乗数も表示します。
fprintf('The objective function value is %d.\nThe number of iterations is %d.\nThe Lagrange multiplier is %d.\n',... fval,output.iterations,lambda.ineqlin)
The objective function value is -3.133073e+10. The number of iterations is 7. The Lagrange multiplier is 1.500050e+04.
下限、上限、線形等式のいずれの制約もないため、有効なラグランジュ乗数は lambda.ineqlin のみです。lambda.ineqlin が非ゼロであるため、不等式制約がアクティブであることがわかります。制約を評価して、解が境界上であることを確認します。
fprintf('The linear inequality constraint A*x has value %d.\n',A*x)The linear inequality constraint A*x has value 9.150244e-08.
解の構成要素の合計は 0 で、許容誤差の範囲内です。
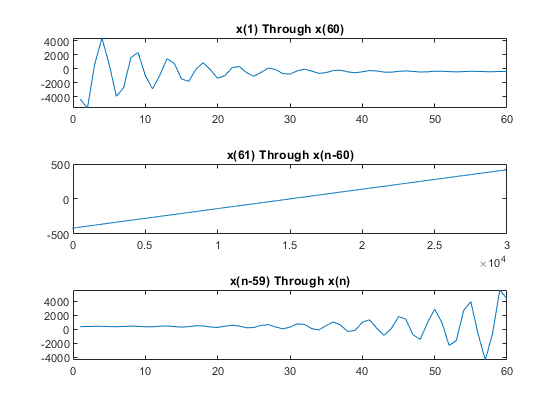
解 x には 3 つの領域、最初の部分、最後の部分、および解の大半を占めるほぼ線形の部分があります。3 つの領域をプロットします。
subplot(3,1,1) plot(x(1:60)) title('x(1) Through x(60)') subplot(3,1,2) plot(x(61:n-60)) title('x(61) Through x(n-60)') subplot(3,1,3) plot(x(n-59:n)) title('x(n-59) Through x(n)')