And 制約に代わる Or 制約の使用

一般的に、ソルバーは次のような暗黙的 AND による制約を受け入れます。

制約 1 AND 制約 2 AND 制約 3 がすべて満たされる。

しかし、次のように OR を使用するのが望ましい場合もあります。

制約 1 OR 制約 2 OR 制約 3 が満たされる。

これらの定式化は論理的に等価ではなく、一般に、OR 制約を AND 制約で表現する方法はありません。

ヒント

幸い、非線形制約は非常に柔軟です。非線形関数を制約関数の最小値に設定するだけで、OR 制約は実現されます。

最小値を制約として設定できる理由は非線形制約の性質にあります。与える制約は、実行可能な点において負になるべき一連の関数となります。次のような制約があるとします。

F₁(x) ≤ 0 OR F₂(x) ≤ 0 OR F₃(x) ≤ 0

この場合は、非線形不等式制約関数 c(x) を次のように設定します。

c(x) = min(F₁(x),F₂(x),F₃(x))

最小値のため、c(x) は滑らかではありません。これは制約関数における一般的な要件です。しかし、この方法は多くの場合うまく機能します。

メモ

OR 制約で通常の範囲や線形制約を使用することはできません。代わりに、この例のように範囲と線形制約を非線形制約関数に変換します。

たとえば、実行可能領域が L 字型の領域だとします。x は四角形 –1 ≤ x(1) ≤ 1, 0 ≤ x(2) ≤ 1 の内部に存在するか、x は四角形 0 ≤ x(1) ≤ 1, –1 ≤ x(2) ≤ 1 の内部に存在します (OR 制約)。

Figure を作成するコード

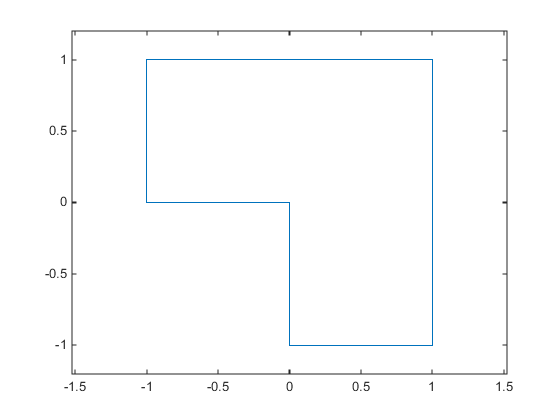
四角形を範囲の制約ではなく非線形制約として表現するために、四角形 a ≤ x(1) ≤ b, c ≤ x(2) ≤ d の内部で負値をとる関数を作成します。

function cout = rectconstr(x,a,b,c,d)
% Negative when  x is in the rectangle [a,b][c,d]
% First check that a,b,c,d are in the correct order

if (b <= a) || (d <= c)
    error('Give a rectangle a < b, c < d')
end

cout = max([(x(1)-b),(x(2)-d),(a-x(1)),(c-x(2))]);

非線形制約関数の最小値を使用する規定に従うと、L 字型の領域で非線形制約関数は次のようになります。

function [c,ceq] = rectconstrfcn(x)

ceq = []; % no equality constraint
F(1) = rectconstr(x,-1,1,0,1); % one rectangle
F(2) = rectconstr(x,0,1,-1,1); % another rectangle
c = min(F); % for OR constraints

Figure を作成するコード

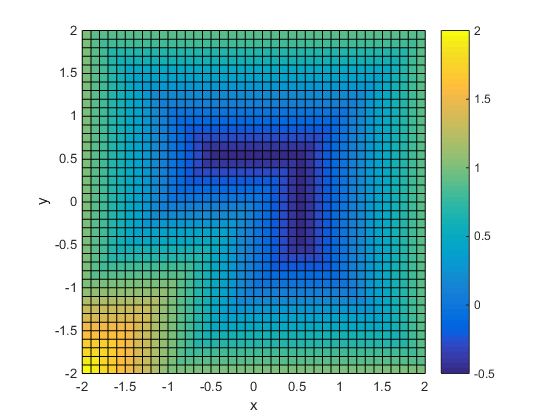
次のような目的関数について考えます。

fun = @(x)exp(x(1)) * (4*x(1)^2 + 2*x(2)^2 + 4*x(1)*x(2) + 2*x(2) + 1);

fun を L 字型の領域で最小化します。

opts = optimoptions(@fmincon,'Algorithm','interior-point','Display','off');
x0 = [-.5,.6]; % an arbitrary guess
[xsol,fval,eflag] = fmincon(fun,x0,[],[],[],[],[],[],@rectconstrfcn,opts)

xsol =

    0.4998   -0.9996


fval =

   2.4650e-07


eflag =

     1

明らかに、解 xsol は L 字型領域の内部にあります。終了フラグは 1 で、xsol が局所的最小値であることを示しています。

参考

fmincon

And 制約に代わる Or 制約の使用

参考

関連するトピック