quad2d

2 重積分の数値的評価 — tiled 法

構文

q = quad2d(fun,a,b,c,d)

q = quad2d(fun,a,b,c,d,Name,Value)

[q,E] = quad2d(___)

説明

q = quad2d(fun,a,b,c,d) は、平面領域 $$a\le x\le b$$ および $$c(x)\le y\le d(x)$$ で fun(x,y) の積分を近似します。境界 c および d はそれぞれスカラーまたは関数ハンドルにすることができます。

q = quad2d(fun,a,b,c,d,Name,Value) は、1 つ以上の Name,Value のペアの引数を使用して追加オプションを指定します。たとえば、'AbsTol' と 'RelTol' を指定して、アルゴリズムが満たさなければならない誤差のしきい値を調整できます。

[q,E] = quad2d(___) は、絶対誤差 E = | q - I | の上限の近似値も返します。ここで、I は正確な積分値です。

例

2 重積分を評価

次の積分を行います。

$$y\sin (x)+x\cos (y)$$

領域は $$-\pi \le x\le 2\pi$$ と $$0\le y\le \pi$$ です。

fun = @(x,y) y.*sin(x)+x.*cos(y);
Q = quad2d(fun,pi,2*pi,0,pi)

Q = 
-9.8696

結果を積分の真の値 $$-{\pi }^2$$ と比較します。

-pi^2

ans = 
-9.8696

積分境界上に特異点がある被積分関数

関数

$${\left[{(x+y)}^{1/2}{(1+x+y)}^2\right]}^{-1}$$

を $$0\le x\le 1$$ および $$0\le y\le 1-x$$ の領域で積分します。この被積分関数は原点 (0,0) で無限であり、これは積分領域の境界上に位置します。

fun = @(x,y) 1./(sqrt(x + y) .* (1 + x + y).^2 );
ymax = @(x) 1 - x;
Q = quad2d(fun,0,1,0,ymax)

Q = 
0.2854

積分の真の値は $$\pi /4-1/2$$ です。

pi/4 - 0.5

ans = 
0.2854

quad2d の制限

quad2d はまず、積分領域を四角形にマッピングします。その結果、4 辺をもたない領域や滑らかに直線にマッピングできない辺をもつ領域上での積分が困難になる場合があります。積分ができない場合の対処法として、Singular を既定値の true に設定したままにするか、直交座標と極座標を変更するか、積分領域を部分に分割して、部分に対する積分結果を加算することをお勧めします。

次に例を示します。

fun = @(x,y)abs(x.^2 + y.^2 - 0.25);
c = @(x)-sqrt(1 - x.^2);
d = @(x)sqrt(1 - x.^2);
quad2d(fun,-1,1,c,d,'AbsTol',1e-8,...
    'FailurePlot',true,'Singular',false);

Warning: Reached the maximum number of function evaluations (2000). The result fails the global error test.

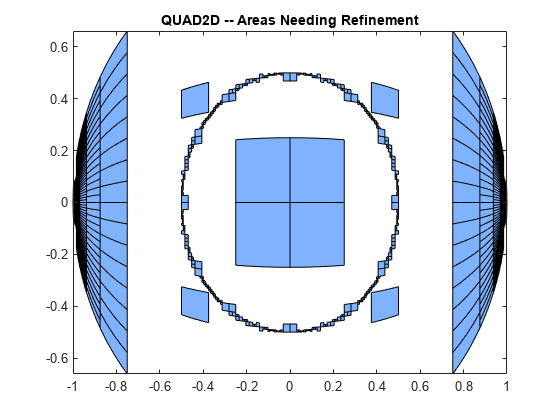
失敗のプロットは、点 (-1,0) および (1,0) 付近と円 $$x^2+y^2=0.25$$ 付近の難易度の高い 2 つの領域を示しています。

Singular の値を true に変更すると、(-1,0) および (1,0) での形状の特異性を扱うことができます。陰影の付いた大きい領域には、微調整が必要な場合がありますが、難易度の高い領域ではない可能性があります。

Q = quad2d(fun,-1,1,c,d,'AbsTol',1e-8, ... 
     'FailurePlot',true,'Singular',true);

Warning: Reached the maximum number of function evaluations (2000). The result passes the global error test.

ここから対称性を利用できます。

Q = 4*quad2d(fun,0,1,0,d,'Abstol',1e-8,...
     'Singular',true,'FailurePlot',true)

Q = 
0.9817

ただし、このコードでは、特異性のある領域付近での処理がまだ困難です。高い精度を達成できない可能性があります。

Q = 4*quad2d(fun,0,1,0,d,'Abstol',1e-10,...
     'Singular',true,'FailurePlot',true);

Warning: Reached the maximum number of function evaluations (2000). The result passes the global error test.

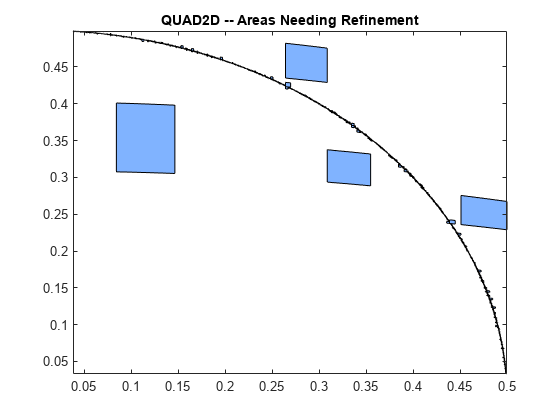
高い精度では、座標の変更がうまく機能する場合があります。

polarfun = @(theta,r) fun(r.*cos(theta),r.*sin(theta)).*r;
Q = 4*quad2d(polarfun,0,pi/2,0,1,'AbsTol',1e-10);

積分領域を 2 つの部分に分割することによって、特異性を境界に配置することをお勧めします。

Q1 = 4*quad2d(polarfun,0,pi/2,0,0.5,'AbsTol',5e-11);
Q2 = 4*quad2d(polarfun,0,pi/2,0.5,1,'AbsTol',5e-11);
Q = Q1 + Q2;

入力引数

fun — 被積分関数

関数ハンドル

被積分関数。関数ハンドルとして指定します。関数 Z = fun(X,Y) は、同じサイズの 2 次元行列 X と Y を受け入れて、対応する値の行列 Z を返さなければなりません。そのため、この関数をベクトル化しなければなりません (つまり、^ などの行列演算子ではなく、.^ などの要素単位の演算子を使用しなければなりません)。この関数の入力と出力は、単精度または倍精度のいずれかでなければなりません。

例: @(x,y) x.^2 - y.^2

データ型: function_handle

a,b — x の積分範囲

スカラー

x の積分範囲。スカラーとして指定します。

データ型: single | double
複素数のサポート: あり

c,d — y の積分範囲

スカラー | 関数ハンドル

y の積分範囲。スカラーまたは関数ハンドルとして指定します。上下限値のそれぞれをスカラーまたは関数ハンドルとして指定できます。範囲を関数ハンドルとして指定する場合、範囲は x の積分範囲の関数 ymin = @x c(x) および ymax = @(x) d(x) です。関数ハンドル ymin および ymax は、行列を受け入れ、対応する値をもつ同じサイズの行列を返さなければなりません。これらの関数の入力と出力は、単精度または倍精度のいずれかでなければなりません。

データ型: single | double | function_handle
複素数のサポート: あり

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

R2021a より前では、コンマを使用して名前と値をそれぞれ区切り、Name を引用符で囲みます。

例: quad2d(@(x,y) x.*y.^2, 0, 1, 0, 2, 'AbsTol',1e-3) は、積分の絶対許容誤差を 1e-3 として指定します。

AbsTol — 絶対許容誤差

1e-5 (既定値) | スカラー

絶対許容誤差。'AbsTol' とスカラーで構成されるコンマ区切りのペアとして指定します。

quad2d は、ERRBND <= max(AbsTol,RelTol*|Q|) の条件を満たそうとします。これは、|Q| が十分に小さいときに絶対誤差を制御し、|Q| が大きいときは相対誤差を制御します。許容誤差が指定されていない場合は、既定の許容誤差の値が使用されます。AbsTol の既定値は 1e-5 です。RelTol の既定値は 100*eps(class(Q)) です。これは、RelTol の最小値でもあります。RelTol の値が小さいと、既定値が自動的に大きくなります。

RelTol — 相対許容誤差

100*eps(class(q)) (既定値) | スカラー

相対許容誤差。'RelTol' とスカラーで構成されるコンマ区切りのペアとして指定します。

quad2d は、ERRBND <= max(AbsTol,RelTol*|Q|) の条件を満たそうとします。これは、|Q| が十分に小さいときに絶対誤差を制御し、|Q| が大きいときは相対誤差を制御します。許容誤差が指定されていない場合は、既定の許容誤差の値が使用されます。AbsTol の既定値は 1e-5 です。RelTol の既定値は 100*eps(class(Q)) です。これは、RelTol の最小値でもあります。RelTol の値が小さいと、既定値が自動的に大きくなります。

MaxFunEvals — fun の最大評価回数

2000 (既定値) | スカラー

fun の最大評価回数。'MaxFunEvals' とスカラーで構成されるコンマ区切りのペアとして指定します。このオプションを使用して、quad2d が関数 fun を評価する回数を制限します。

FailurePlot — 失敗のプロットを生成するかどうかの切り替え

false または 0 (既定値) | true または 1

失敗のプロットを生成するかどうかの切り替え。'FailurePlot' と、数値または logical の 1 (true) または 0 (false) で構成されるコンマ区切りのペアとして指定します。FailurePlot を true または 1 に設定すると、MaxFunEvals に達した場合にさらに調整の必要な領域のグラフィカルな表現が生成されます。MaxFunEvals に達する前に積分が終了する場合はプロットが生成されません。失敗のプロットには (一般的に) 4 辺で囲まれた領域があり、これは内部で四角形にマッピングされます。小さい領域の集まりは、積分の難易度の高い領域を示します。

Singular — 境界特異性を変換するかどうかの切り替え

true または 1 (既定値) | false または 0

境界特異性を変換するかどうかの切り替え。'Singular' と、数値または logical の 1 (true) または 0 (false) で構成されるコンマ区切りのペアとして指定します。既定で、quad2d はパフォーマンスを向上させるために、境界特異性を弱くする変換を使用します。'Singular' を false または 0 に設定すると、この変換はオフになり、一部の滑らかさの問題でパフォーマンス上のメリットが得られます。

出力引数

q — 計算された積分

スカラー

計算された積分。スカラーとして返されます。

E — 誤差範囲

スカラー

誤差範囲。スカラーとして返されます。誤差範囲は、計算された積分 q と、積分 I の正確な値との誤差の上限を指定するもので、E = | q - I | です。

参照

[1] L.F. Shampine, "MATLAB Program for Quadrature in 2D." Applied Mathematics and Computation. Vol. 202, Issue 1, 2008, pp. 266–274.

拡張機能

C/C++ コード生成

MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意および制限:

• 生成されたコードは、内部ストレージ配列のサイズが足りない場合に警告を発行します。警告が発生した場合の回避策として、積分領域を分割し、各分割領域で積分の和をとることができます。

バージョン履歴

R2009a で導入

参考

quadgk | integral | integral2 | integral3

トピック

• 無名関数
• 関数ハンドルの作成