FFT を使った多項式内挿

高速フーリエ変換 (FFT) を使用して、一連のデータを内挿する三角多項式の係数を推定します。

数学における FFT

FFT アルゴリズムは信号処理アプリケーションに関連付けられていますが、数学における高速計算ツールとして、より一般的な使用もできます。たとえば、一連のデータを内挿する n 次多項式 $c_{1} x^{n} + c_{2} x^{n - 1} + ... + c_{n} x + c_{n + 1}$ の係数 c_i は、一般的に、簡単な連立線形方程式を解くことによって計算されます。19 世紀初頭、Carl Friedrich Gauss は小惑星の軌道を研究しているときに、問題をより小さい部分問題に分割し、結果をまとめることによって多項式内挿の係数を計算するための数学による簡便な手法を発見しました。この手法は、データの離散フーリエ変換を推定することと等価でした。

小惑星データの内挿

ライブスクリプトを開く

Gauss は論文の中で、小惑星パラスの軌道を推定する方法を説明しています。彼はまず、以下の 12 個の 2 次元位置データ点 x および y から始めます。

x = 0:30:330;
y = [408 89 -66 10 338 807 1238 1511 1583 1462 1183 804];
plot(x,y,'ro')
xlim([0 360])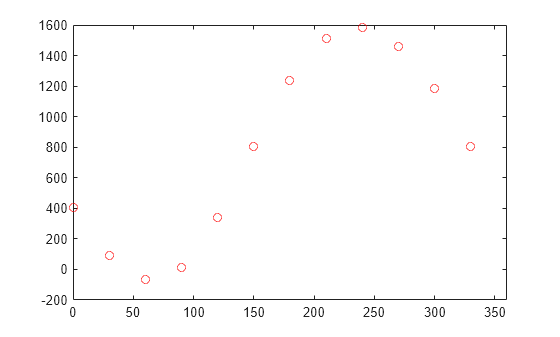

Figure contains an axes object. The axes contains a line object which displays its values using only markers.

Gauss は次の形式の三角多項式で小惑星の軌道をモデル化しています。

$\begin{array}{rcl} y = a_{0} & + & a_{1} \cos (2 π (x / 360)) + b_{1} \sin (2 π (x / 360)) \\ a_{2} \cos (2 π (2 x / 360)) + b_{2} \sin (2 π (2 x / 360)) \\ \dots \\ a_{5} \cos (2 π (5 x / 360)) + b_{5} \sin (2 π (5 x / 360)) \\ a_{6} \cos (2 π (6 x / 360)) \end{array}$

fft を使用して多項式の係数を計算します。

m = length(y);
n = floor((m+1)/2);
z = fft(y)/m;

a0 = z(1); 
an = 2*real(z(2:n));
a6 = z(n+1);
bn = -2*imag(z(2:n));

元のデータ点に重ねて内挿多項式をプロットします。

hold on
px = 0:0.01:360;
k = 1:length(an);
py = a0 + an*cos(2*pi*k'*px/360) ...
        + bn*sin(2*pi*k'*px/360) ...
        + a6*cos(2*pi*6*px/360); 

plot(px,py)

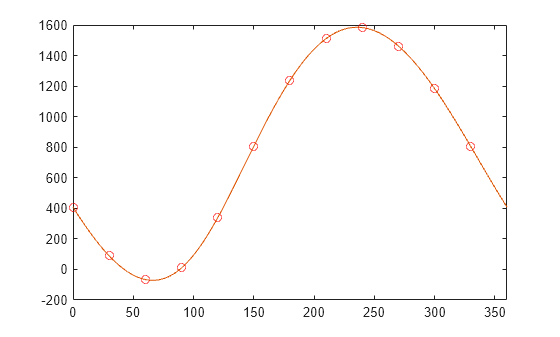
Figure contains an axes object. The axes object contains 2 objects of type line. One or more of the lines displays its values using only markers

参照

[1] Briggs, W. and V.E. Henson. The DFT: An Owner's Manual for the Discrete Fourier Transform. Philadelphia: SIAM, 1995.

[2] Gauss, C. F. “Theoria interpolationis methodo nova tractata.” Carl Friedrich Gauss Werke. Band 3. Göttingen: Königlichen Gesellschaft der Wissenschaften, 1866.

[3] Heideman M., D. Johnson, and C. Burrus. “Gauss and the History of the Fast Fourier Transform.” Arch. Hist. Exact Sciences. Vol. 34. 1985, pp. 265–277.

[4] Goldstine, H. H. A History of Numerical Analysis from the 16th through the 19th Century. Berlin: Springer-Verlag, 1977.

参考

fft

トピック

フーリエ変換