このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

逆ラドン変換

逆ラドン変換の定義

関数 iradon はラドン変換の逆変換を行うため、イメージの再構成に使用できます。

ラドン変換の説明に従って、イメージ I と角度 theta を与えて、関数 radon はラドン変換を計算します。

R = radon(I,theta);

関数 iradon はその後で、投影データからイメージ I を再構成するために呼び出されます。

IR = iradon(R,theta);

上の例の中で、投影は元のイメージ I から計算されます。

ただし、大部分のアプリケーション エリアでは、投影されたものから元のイメージを作ることはできません。たとえば、逆ラドン変換は通常、断層撮影のアプリケーションで使用されます。X 線による吸収断層撮影では、異なる角度で物理的な標本を通過する放射線減衰の測定により投影が行われます。元のイメージは、密度が強度値によって表される標本の断面であると考えることができます。映像は特別な目的で設計されたハードウェアで収集され、標本の内部イメージが関数 iradon によって再構成されます。この方法は、生体の内部や不透明な物体の内部の断層撮影技術で使用することができます。

iradon は、パラレル ビーム投影によりイメージを再構成します。"パラレル ビーム形状" では、各投影は、指定した角度でイメージを通った一連の線積分を組み合わせて形成されます。

次の図は、パラレル ビーム形状が X 線の吸収断層撮影への適用にどのように使用されるかを示しています。"n" 個のエミッターと "n" 個のセンサーがあることに注目してください。個々のセンサーは、対応するエミッターからの放射量を測定し、放射による減衰が物体の全体の密度または質量の尺度を与えます。これは、ラドン変換で計算される線積分に対応します。

図で使用されているパラレル ビーム形状は、ラドン変換で説明されている形状と同じです。f(x,y) はイメージの明度を示し、$$R_{\theta }(x\prime )$$ は角度 θ での投影です。

オブジェクトを通るパラレル ビーム投影

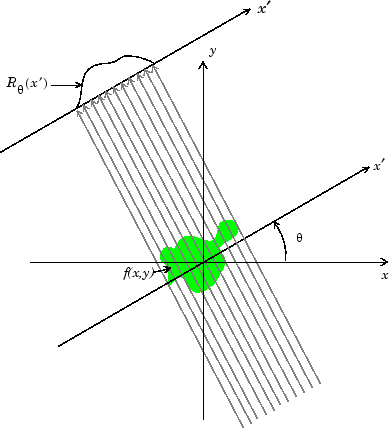
一般に使用されるもう 1 つの形状は "ファンビーム" 形状です。これは、1 つのエミッターに対して "n" 個のセンサーを使用しています。詳細については、ファンビーム投影を参照してください。パラレル ビーム投影データをファンビーム投影データに変換するには、関数 para2fan を使用します。

結果の改良

iradon は、"フィルター補正逆投影法" アルゴリズムを使用して、逆ラドン変換を計算します。このアルゴリズムは、投影をベースにして、イメージ I の近似を R の列の中に設定しています。詳細な結果は、再構成の中で多くの投影を使用することにより得ることができます。投影の数 (theta の長さ) を増加させると、再構成されたイメージ IR は元のイメージ I により近似します。ベクトル theta には一定の増分角度 Dtheta で単調増加する角度が含まれていなければなりません。スカラー Dtheta が既知の場合は、theta 値の配列の代わりにそれを iradon に渡すこともできます。次に例を示します。

IR = iradon(R,Dtheta);

フィルター補正逆投影法アルゴリズムは、R の中の投影にフィルターを適用し、適用された投影を使用してイメージを再構成します。多くの場合、投影の中にはノイズが含まれています。高周波ノイズを除去するには、ノイズを減少させるためにウィンドウをフィルターに適用します。このようなウィンドウをもつフィルターも、関数 iradon にあります。次の iradon の例は、ハミング ウィンドウをフィルターに適用しています。詳細については、iradon のリファレンス ページを参照してください。フィルター補正なしの逆投影データを取得するには、フィルター パラメーターに "none" を指定します。

IR = iradon(R,theta,"Hamming");

関数 iradon は正規化した周波数 D も設定できます。これは、これより上の周波数で、フィルターの応答をゼロにしています。D は [0,1] の間のスカラー値でなければなりません。このオプションを使用して、周波数軸は再度スケーリングされ、フィルター全体が周波数の範囲 [0,D] で適合するように圧縮されます。これは、投影にあまり高周波数の情報が含まれてなく、含まれていた場合でも、それが高周波のノイズである場合に役立ちます。この場合、ノイズは再構成のために処理を行わなくても、完全に低減させることができます。次の iradon を呼び出すと、正規化した周波数値が 0.85 に設定されます。

IR = iradon(R,theta,0.85);

平行投影データからのイメージの再構成

この例では、平行投影データからイメージを再構成する方法と、再構成されるイメージの画質が投影角度を増やすことによってどのように改善されるのかを説明します。

関数 phantom を使用して、Shepp-Logan の頭部ファントム イメージを作成します。ファントム イメージは、人頭の実際の断層撮影イメージで見られるさまざまな要素を示します。外側の明るい楕円の外殻は頭蓋骨と考えられ、内部の多くの楕円は脳の特徴と考えられます。

P = phantom(256);
imshow(P)

ファントム脳のラドン変換を、3 種類の θ 値に対して計算します。R1 は 18 投影、R2 は 36 投影、R3 は 90 投影とします。

theta1 = 0:10:170; [R1,xp] = radon(P,theta1);
theta2 = 0:5:175;  [R2,xp] = radon(P,theta2);
theta3 = 0:2:178;  [R3,xp] = radon(P,theta3);

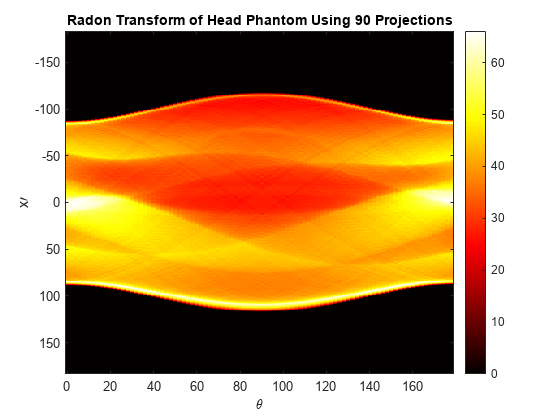
90 投影の Shepp-Logan 頭部ファントムのラドン変換をプロットします。入力イメージの中の特徴が、変換のこのイメージの中でどのように現れているかを確認してください。ラドン変換の最初の列は、垂直方向への積分 0 度での投影に対応します。真ん中の列は 90 度での投影に対応し、水平方向に積分します。90 度での投影は、ファントムの最も外側の楕円の垂直半軸が長いため、0 度での投影に比べてプロファイルの幅が広くなります。

figure
imagesc(theta3,xp,R3) 
colormap(hot); colorbar
xlabel('\theta'); ylabel('x\prime')
title("Radon Transform of Head Phantom Using 90 Projections")

3 セットの投影データから、3 個の頭部ファントム イメージを再構成します。

I1 = iradon(R1,10);
I2 = iradon(R2,5);
I3 = iradon(R3,2);

結果をモンタージュに表示します。左側のイメージ I1 の精度が一番悪く見えます。これは、たった 18 の投影から再構成したものです。36 の投影から再構成した中央のイメージ I2 は少し良く見えますが、イメージ下部の小さな楕円を区別できるほど鮮明ではありません。90 の投影を使用して再構成した右側のイメージ I3 は、元のイメージに最も近いものが出力されています。(I1 および I2 に示すように) 投影数が比較的少ない場合、再構成は逆変換で複数のアーティファクトを生じることに注目してください。

montage({I1,I2,I3},Size=[1 3])