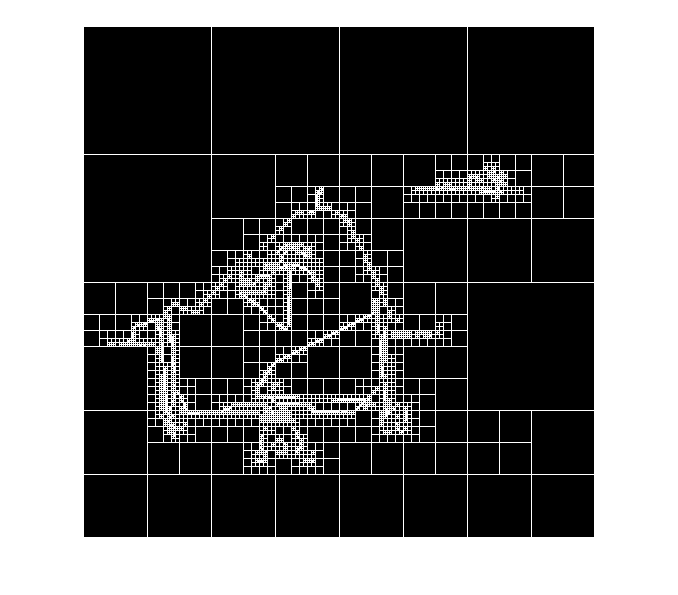四分木分割

四分木分割は、イメージを分割して、イメージ全体の均一性より高い均一性をもつブロックに細分割する解析手法です。この手法によってイメージの構造に関する情報を取得します。これは適応圧縮アルゴリズムでの最初のステップとしても役に立ちます。

四分木分割は、関数 qtdecomp を使用して行います。この関数は、四角いイメージを同じサイズの四角いブロックに四等分し、各ブロックが指定された均一性条件を満たすかどうか (たとえば、ブロック内のすべてのピクセルが指定されたダイナミック レンジ内にあるかどうか) をテストすることによって機能します。ブロックが条件を満たしている場合、それ以上の分割は行いません。条件を満たしていない場合、そのブロックをさらに 4 ブロックに分割し、それらのブロックにテスト条件を適用します。このプロセスを、各ブロックが条件を満たすまで繰り返します。その結果、異なる大きさのブロックができます。細分化されたブロックの最小サイズは 1 行 1 列まで可能ですが、最小サイズは指定できます。

qtdecomp は四分木分割をスパース行列として返します。これは I と同じサイズです。非ゼロ要素はブロックの左上を表します。各非ゼロ要素の値はそのブロックのサイズを示します。

イメージの四分木分割

この例では、512 行 512 列のグレースケール イメージを四分木分割する方法を説明します。

グレースケール イメージをワークスペースに読み取ります。

I = imread('liftingbody.png');

イメージと、四分木分割された各ブロックの均一性テストに使用する条件を指定して関数 qtdecomp を呼び出し、四分木分割を実行します。たとえば、条件には max(block(:)) - min(block(:)) >= 0.27 などのしきい値計算を使用できます。また、ブロックを分割するかどうかを決定するしきい値の代わりに関数を qtdecomp に渡すこともできます。たとえば、ブロックの分散値に基づいて決定することもできます。

S = qtdecomp(I,0.27);

四分木分割のブロック表現を表示します。個々の黒い四角は均一ブロックを表し、白い線はブロック間の境界を表します。イメージ強度の大きな変化に対応する領域ではブロックが小さくなっています。

blocks = repmat(uint8(0),size(S));

for dim = [512 256 128 64 32 16 8 4 2 1];    
  numblocks = length(find(S==dim));    
  if (numblocks > 0)        
    values = repmat(uint8(1),[dim dim numblocks]);
    values(2:dim,2:dim,:) = 0;
    blocks = qtsetblk(blocks,S,dim,values);
  end
end

blocks(end,1:end) = 1;
blocks(1:end,end) = 1;

imshow(I), figure, imshow(blocks,[])

参考

qtdecomp