アンセンテッドカルマンフィルターおよび粒子フィルターを使用した非線形の状態推定

この例では次を使用します。

ライブスクリプトを開く

この例では、ファンデルポール振動子の非線形の状態推定に対して、アンセンテッドカルマンフィルターおよび粒子フィルターアルゴリズムを使用する方法を説明します。

この例では Signal Processing Toolbox™ も使用します。

はじめに

System Identification Toolbox™ は、非線形の状態推定に使用できる 3 つのコマンドを提供します。

extendedKalmanFilter:1 次離散時間の拡張カルマンフィルター
unscentedKalmanFilter:離散時間のアンセンテッドカルマンフィルター
particleFilter:離散時間粒子フィルター

これらのコマンドの使用に関する一般的なワークフローは次のとおりです。

プラントとセンサーの動作をモデル化します。
extendedKalmanFilter、unscentedKalmanFilter または particleFilter オブジェクトを作成して構成します。
このオブジェクトを指定して predict コマンドと correct コマンドを使用し、状態推定を実行します。
結果を解析し、フィルターのパフォーマンスを確認します。
ハードウェアにフィルターを展開します。MATLAB® Coder™ を使用すると、これらのフィルターのコードを生成できます。

この例では、まず unscentedKalmanFilter コマンドを使用して、このワークフローについて説明します。その後、particleFilter の使用方法を説明します。

プラントのモデル化と離散化

アンセンテッドカルマンフィルター (UKF) アルゴリズムには、タイムステップ間の状態の変化を記述する関数が必要です。一般的にこれは状態遷移関数と呼ばれます。unscentedKalmanFilter は次の 2 つの関数形式をサポートします。

加法性のプロセスノイズ: $x [k] = f (x [k - 1], u [k - 1]) + w [k - 1]$
非加法性のプロセスノイズ: $x [k] = f (x [k - 1], w [k - 1], u [k - 1])$

ここで、f(..) は状態遷移関数、x は状態、w はプロセスノイズです。u はオプションで、f に対する追加入力を表しています (たとえば、システム入力やパラメーター)。u には 0 個以上の関数引数を指定できます。加法性ノイズは、状態とプロセスノイズが線形的に関係していることを意味します。関係が非線形である場合は、2 番目の形式を使用します。unscentedKalmanFilter オブジェクトを作成する場合、f(..) に加えて、プロセスノイズが加法性または非加法性のいずれであるかも指定します。

この例のシステムは、mu=1 のファンデルポール振動子です。この 2 状態システムは、次の非線形の常微分方程式 (ODE) で記述されます。

$\begin{array}{l} {x_{}^{˙}}_{1} = x_{2} \\ {x_{}^{˙}}_{2} = (1 - x_{1}^{2}) x_{2} - x_{1} \end{array}$

この方程式を $x_{}^{˙} = f_{c} (x)$ と表します。ここで、 $x = [x_{1}; x_{2}]$ です。プロセスノイズ w はシステムモデルには現れません。単純化するために、このプロセスノイズは加法性であると仮定します。

unscentedKalmanFilter は離散時間状態遷移関数を必要としますが、プラントモデルは連続時間です。この連続時間モデルに離散時間近似を使用できます。オイラー法による離散化は一般的な近似手法の 1 つです。サンプル時間は $T_{s}$ であると仮定し、連続時間のダイナミクスを $x_{}^{˙} = f_{c} (x)$ として表します。オイラー法による離散化では、微分演算子を $x_{}^{˙} \approx \frac{x [k + 1] - x [k]}{T_{s}}$ として近似します。結果の離散時間状態遷移関数は次のようになります。

$\begin{array}{ll} x [k + 1] & = x [k] + f_{c} (x [k]) T_{s} \\ = f (x [k]) \end{array}$

この近似の精度は、サンプル時間 $T_{s}$ によって変わります。 $T_{s}$ の値が小さいほど、近似の精度が高まります。また、異なる離散化手法を使用することもできます。たとえば、ルンゲ・クッタ法は、固定のサンプル時間 $T_{s}$ が与えられた場合、次数が高いほど計算コストは高くなりますが、より高い精度が得られます。

この状態遷移関数を作成し、vdpStateFcn.m という名前のファイルに保存します。サンプル時間 $T_{s} = 0.05 s$ を使用します。オブジェクトの作成中、この関数を unscentedKalmanFilter に提供します。

type vdpStateFcn

function x = vdpStateFcn(x) 
% vdpStateFcn Discrete-time approximation to van der Pol ODEs for mu = 1. 
% Sample time is 0.05s.
%
% Example state transition function for discrete-time nonlinear state
% estimators.
%
% xk1 = vdpStateFcn(xk)
%
% Inputs:
%    xk - States x[k]
%
% Outputs:
%    xk1 - Propagated states x[k+1]
%
% See also extendedKalmanFilter, unscentedKalmanFilter

%   Copyright 2016 The MathWorks, Inc.

%#codegen

% The tag %#codegen must be included if you wish to generate code with 
% MATLAB Coder.

% Euler integration of continuous-time dynamics x'=f(x) with sample time dt
dt = 0.05; % [s] Sample time
x = x + vdpStateFcnContinuous(x)*dt;
end

function dxdt = vdpStateFcnContinuous(x)
%vdpStateFcnContinuous Evaluate the van der Pol ODEs for mu = 1
dxdt = [x(2); (1-x(1)^2)*x(2)-x(1)];
end

センサーモデリング

unscentedKalmanFilter には、モデルの状態がセンサー測定値にどのように関係しているかを記述する関数も必要です。unscentedKalmanFilter は次の 2 つの関数形式をサポートします。

加法性の測定ノイズ: $y [k] = h (x [k], u [k]) + v [k]$
非加法性の測定ノイズ: $y [k] = h (x [k], v [k], u [k])$

h(..) は測定関数、v は測定ノイズです。u はオプションで、h に対する追加入力を表しています (たとえば、システム入力やパラメーター)。u には 0 個以上の関数引数を指定できます。u 項の後に追加のシステム入力を指定できます。これらの入力は、状態遷移関数の入力とは異なるものを指定できます。

この例では、最初の状態 $x_{1}$ の測定の誤差が数パーセント以内であると仮定します。

$y [k] = x_{1} [k] (1 + v [k])$

測定ノイズが単に状態の関数に追加されることはないため、これは非加法性の測定ノイズのカテゴリに分類されます。ノイズを含む測定値から $x_{1}$ と $x_{2}$ の両方を推定します。

この状態遷移関数を作成し、vdpMeasurementNonAdditiveNoiseFcn.m という名前のファイルに保存します。オブジェクトの作成中、この関数を unscented に提供します。

type vdpMeasurementNonAdditiveNoiseFcn

function yk = vdpMeasurementNonAdditiveNoiseFcn(xk,vk)
% vdpMeasurementNonAdditiveNoiseFcn Example measurement function for discrete
% time nonlinear state estimators with non-additive measurement noise.
%
% yk = vdpNonAdditiveMeasurementFcn(xk,vk)
%
% Inputs:
%    xk - x[k], states at time k
%    vk - v[k], measurement noise at time k
%
% Outputs:
%    yk - y[k], measurements at time k
%
% The measurement is the first state with multiplicative noise
%
% See also extendedKalmanFilter, unscentedKalmanFilter

%   Copyright 2016 The MathWorks, Inc.

%#codegen

% The tag %#codegen must be included if you wish to generate code with 
% MATLAB Coder.

yk = xk(1)*(1+vk);
end

アンセンテッドカルマンフィルターの構築

状態遷移関数および測定関数に対する関数ハンドル、次に初期状態の推定値を指定することで、フィルターを構築します。状態遷移モデルには加法性ノイズがあります。これはフィルターの既定の設定であるため、指定する必要はありません。測定モデルには非加法性ノイズがあり、オブジェクトの HasAdditiveMeasurementNoise プロパティを false に設定することで指定しなければなりません。この操作は、オブジェクトの作成中に行わなければなりません。アプリケーションの状態遷移関数に非加法性のプロセスノイズがある場合、HasAdditiveProcessNoise プロパティを false に指定します。

% Your initial state guess at time k, utilizing measurements up to time k-1: xhat[k|k-1]
initialStateGuess = [2;0]; % xhat[k|k-1]
% Construct the filter
ukf = unscentedKalmanFilter(...
    @vdpStateFcn,... % State transition function
    @vdpMeasurementNonAdditiveNoiseFcn,... % Measurement function
    initialStateGuess,...
    'HasAdditiveMeasurementNoise',false);

測定ノイズの共分散に関する情報を指定します。

R = 0.2; % Variance of the measurement noise v[k]
ukf.MeasurementNoise = R;

ProcessNoise プロパティは、プロセスノイズの共分散を保存します。このプロパティは、モデルの不正確さや、未知の外乱がプラントに与える影響を説明するために設定されます。この例では実モデルを使用していますが、離散化によって誤差が発生します。単純化するために、この例には外乱が含まれていません。最初の状態ではノイズが少なく、2 番目の状態ではノイズが増加している対角行列に設定することで、2 番目の状態はモデル化誤差の影響を強く受けるという情報を反映させます。

ukf.ProcessNoise = diag([0.02 0.1]);

`predict` コマンドと `correct` コマンドを使用した推定

アプリケーションでは、ハードウェアからリアルタイムで受信した測定データがフィルターによって逐次処理されます。この例では、最初に測定データセットを生成し、次にそのデータをステップごとにフィルターに送ることで、この動作について説明します。

フィルターのサンプル時間を 0.05 [s] に設定し、ファン・デル・ポール振動子を 5 秒間シミュレートすることで、システムの実際の状態を生成します。

T = 0.05; % [s] Filter sample time
timeVector = 0:T:5;
[~,xTrue]=ode45(@vdp1,timeVector,[2;0]);

各測定における標準偏差を 45% の誤差とし、センサーが最初の状態を測定すると仮定して測定値を生成します。

rng(1); % Fix the random number generator for reproducible results
yTrue = xTrue(:,1);
yMeas = yTrue .* (1+sqrt(R)*randn(size(yTrue))); % sqrt(R): Standard deviation of noise

後で解析するデータ用の空間を事前に割り当てます。

Nsteps = numel(yMeas); % Number of time steps
xCorrectedUKF = zeros(Nsteps,2); % Corrected state estimates
PCorrected = zeros(Nsteps,2,2); % Corrected state estimation error covariances
e = zeros(Nsteps,1); % Residuals (or innovations)

correct コマンドと predict コマンドを使用して、状態 x のオンライン推定を実行します。生成されたデータをタイムステップごとにフィルターに提供します。

for k=1:Nsteps
    % Let k denote the current time.
    %
    % Residuals (or innovations): Measured output - Predicted output
    e(k) = yMeas(k) - vdpMeasurementFcn(ukf.State); % ukf.State is x[k|k-1] at this point
    % Incorporate the measurements at time k into the state estimates by
    % using the "correct" command. This updates the State and StateCovariance
    % properties of the filter to contain x[k|k] and P[k|k]. These values
    % are also produced as the output of the "correct" command.
    [xCorrectedUKF(k,:), PCorrected(k,:,:)] = correct(ukf,yMeas(k));
    % Predict the states at next time step, k+1. This updates the State and
    % StateCovariance properties of the filter to contain x[k+1|k] and
    % P[k+1|k]. These will be utilized by the filter at the next time step.
    predict(ukf);
end

アンセンテッドカルマンフィルターの結果と検証

時間の経過に合わせて実際の状態と推定される状態をプロットします。また、最初の状態の測定値もプロットします。

figure();
subplot(2,1,1);
plot(timeVector,xTrue(:,1),timeVector,xCorrectedUKF(:,1),timeVector,yMeas(:));
legend('True','UKF estimate','Measured')
ylim([-2.6 2.6]);
ylabel('x_1');
subplot(2,1,2);
plot(timeVector,xTrue(:,2),timeVector,xCorrectedUKF(:,2));
ylim([-3 1.5]);
xlabel('Time [s]');
ylabel('x_2');

Figure contains 2 axes objects. Axes object 1 with ylabel x_1 contains 3 objects of type line. These objects represent True, UKF estimate, Measured. Axes object 2 with xlabel Time [s], ylabel x_2 contains 2 objects of type line.

上のプロットは、最初の状態に関する真値、推定された値、および測定値を示しています。フィルターはシステムモデルとノイズ共分散に関する情報を利用し、測定値よりも改善された推定値を生成します。下のプロットは 2 番目の状態を示しています。フィルターは適切な推定を正しく生成します。

アンセンテッドまたは拡張カルマンフィルターのパフォーマンス検証は、通常は幅広いモンテカルロ法シミュレーションを使用して実行されます。こうしたシミュレーションでは、次のバリエーションがテストされます。プロセスノイズと測定ノイズの実現、さまざまな条件下でのプラント操作、初期状態および状態共分散の推定。状態推定の検証に使用される主な対象信号は残差 (つまりイノベーション) です。この例では、単一のシミュレーションに対して残差分析を実行します。残差をプロットします。

figure();
plot(timeVector, e);
xlabel('Time [s]');
ylabel('Residual (or innovation)');

Figure contains an axes object. The axes object with xlabel Time [s], ylabel Residual (or innovation) contains an object of type line.

残差は次のとおりとします。

小さい振幅
ゼロ平均
自己相関なし (ラグ 0 を除く)

残差の平均値は次のとおりです。

mean(e)

ans = -0.0012

これは、残差の振幅に比べて小さい値です。残差の自己相関は、Signal Processing Toolbox の関数 xcorr を使用して計算できます。

[xe,xeLags] = xcorr(e,'coeff'); % 'coeff': normalize by the value at zero lag
% Only plot non-negative lags
idx = xeLags>=0;
figure();
plot(xeLags(idx),xe(idx));
xlabel('Lags');
ylabel('Normalized correlation');
title('Autocorrelation of residuals (innovation)');

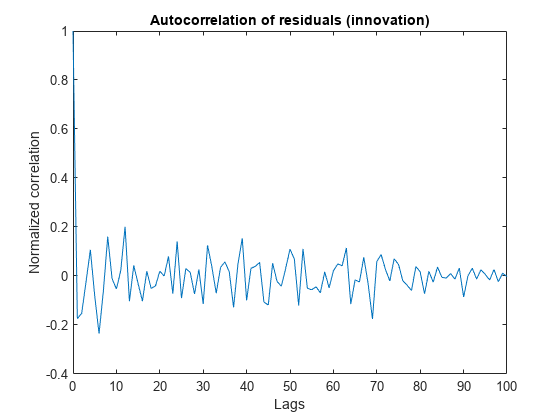
Figure contains an axes object. The axes object with title Autocorrelation of residuals (innovation), xlabel Lags, ylabel Normalized correlation contains an object of type line.

相関は、0 を除くすべてのラグで小さくなっています。相関の平均は 0 に近く、相関にランダムでない大きな変化はありません。こうした特性はフィルターパフォーマンスの信頼度を向上させます。

現実には、実際の状態を見ることはできません。しかし、シミュレーションの実行時に実際の状態にアクセスして、推定された状態と実際の状態の間の誤差を確認することができます。こうした誤差は、次のような残差に対する同様の条件を満たさなければなりません。

小さい振幅
分散がフィルター誤差の共分散推定の範囲内にある
ゼロ平均
相関なし

最初に、フィルター誤差の共分散推定から、誤差範囲と $1 σ$ の不確かさ範囲を確認します。

eStates = xTrue-xCorrectedUKF;
figure();
subplot(2,1,1);
plot(timeVector,eStates(:,1),...               % Error for the first state
    timeVector, sqrt(PCorrected(:,1,1)),'r', ... % 1-sigma upper-bound
    timeVector, -sqrt(PCorrected(:,1,1)),'r');   % 1-sigma lower-bound
xlabel('Time [s]');
ylabel('Error for state 1');
title('State estimation errors');
subplot(2,1,2);
plot(timeVector,eStates(:,2),...               % Error for the second state
    timeVector,sqrt(PCorrected(:,2,2)),'r', ...  % 1-sigma upper-bound
    timeVector,-sqrt(PCorrected(:,2,2)),'r');    % 1-sigma lower-bound
xlabel('Time [s]');
ylabel('Error for state 2');
legend('State estimate','1-sigma uncertainty bound',...
    'Location','Best');

Figure contains 2 axes objects. Axes object 1 with title State estimation errors, xlabel Time [s], ylabel Error for state 1 contains 3 objects of type line. Axes object 2 with xlabel Time [s], ylabel Error for state 2 contains 3 objects of type line. These objects represent State estimate, 1-sigma uncertainty bound.

センサーモデル (MeasurementFcn) なので、t=2.15 秒での状態 1 の誤差範囲は 0 に近づきます。この形式は $x_{1} [k] * (1 + v [k])$ です。t=2.15 秒では、実際の状態および推定された状態は 0 に近くなっています。これは、絶対項での測定値誤差も 0 に近いことを示しています。これはフィルターの状態推定誤差の共分散に反映されます。

何パーセントの点が 1 シグマの不確かさ範囲を超えているかを計算します。

distanceFromBound1 = abs(eStates(:,1))-sqrt(PCorrected(:,1,1));
percentageExceeded1 = nnz(distanceFromBound1>0) / numel(eStates(:,1));
distanceFromBound2 = abs(eStates(:,2))-sqrt(PCorrected(:,2,2));
percentageExceeded2 = nnz(distanceFromBound2>0) / numel(eStates(:,2));
[percentageExceeded1 percentageExceeded2]

ans = 1×2

    0.1386         0

最初の状態推定の誤差は、そのタイムステップにおける $1 σ$ の不確かさ範囲である約 14% を超えています。1 シグマの不確かさ範囲を超えている誤差の 30% 未満が、適切な推定であることを示します。この条件は両方の状態で満たされます。2 番目の状態に対する 0% という割合は、フィルターが保守的であることを意味しています。ほとんどの場合、組み合わせたプロセスノイズと測定ノイズが高すぎます。これらのパラメーターを調整することで、パフォーマンスの向上を実現できる可能性があります。

状態推定誤差の平均の自己相関を計算します。また、自己相関をプロットします。

mean(eStates)

ans = 1×2

   -0.0103    0.0201

[xeStates1,xeStatesLags1] = xcorr(eStates(:,1),'coeff'); % 'coeff': normalize by the value at zero lag
[xeStates2,xeStatesLags2] = xcorr(eStates(:,2),'coeff'); % 'coeff'
% Only plot non-negative lags
idx = xeStatesLags1>=0;
figure();
subplot(2,1,1);
plot(xeStatesLags1(idx),xeStates1(idx));
xlabel('Lags');
ylabel('For state 1');
title('Normalized autocorrelation of state estimation error');
subplot(2,1,2);
plot(xeStatesLags2(idx),xeStates2(idx));
xlabel('Lags');
ylabel('For state 2');

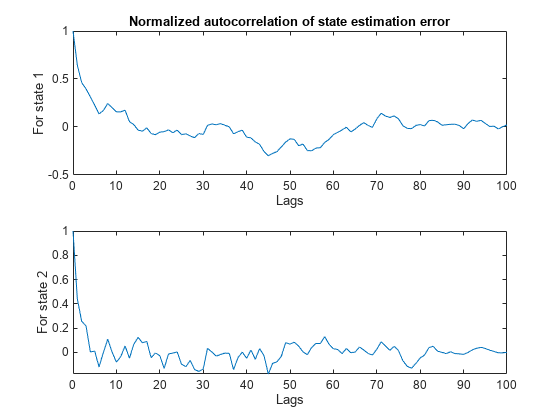
Figure contains 2 axes objects. Axes object 1 with title Normalized autocorrelation of state estimation error, xlabel Lags, ylabel For state 1 contains an object of type line. Axes object 2 with xlabel Lags, ylabel For state 2 contains an object of type line.

誤差の平均値は、状態の値と比べて小さくなっています。状態推定誤差の自己相関は、小さなラグ値に対してランダムでない変化がほとんどないことを示しますが、これらは正規化されたピーク値 1 よりもはるかに小さいものです。推定された状態は正確であるという事実と組み合わせることで、残差に関するこの動作は満足できる結果であると考えることができます。

粒子フィルターの構築

アンセンテッドカルマンフィルターおよび拡張カルマンフィルターは、異なる近似法による状態推定値の事後分布の平均と共分散を追跡することを目的とします。システムの非線形性が著しい場合、これらの手法では十分でないことがあります。また、アプリケーションによっては、状態推定値の事後分布の平均と共分散を追跡するだけでは不十分です。粒子フィルターでは、計算コストが高くなりますが、多くの状態仮説 (粒子) の経時的な変化を追跡することにより、このような問題を解決できます。粒子の数が多いほど、計算コストと推定の精度は高くなります。

System Identification Toolbox の particleFilter コマンドは、離散時間の粒子フィルターアルゴリズムを実装します。この節では、この例で前に使用したのと同じファンデルポール振動子の粒子フィルターを構築する手順を示し、アンセンテッドカルマンフィルターとの類似点および相違点について説明します。

particleFilter に与える状態遷移関数は、次の 2 つのタスクを実行しなければなりません。1. システムに適した分布からのプロセスノイズのサンプリング。2. すべての粒子 (状態仮説) の、次のステップまでの時間伝播の計算。これにはステップ 1 で計算したプロセスノイズの効果も含みます。

type vdpParticleFilterStateFcn

function particles = vdpParticleFilterStateFcn(particles) 
% vdpParticleFilterStateFcn Example state transition function for particle
%                           filter
%
% Discrete-time approximation to van der Pol ODEs for mu = 1. 
% Sample time is 0.05s.
%
% predictedParticles = vdpParticleFilterStateFcn(particles)
%
% Inputs:
%    particles - Particles at current time. Matrix with dimensions
%                [NumberOfStates NumberOfParticles] matrix
%
% Outputs:
%    predictedParticles - Predicted particles for the next time step
%
% See also particleFilter

%   Copyright 2017 The MathWorks, Inc.

%#codegen

% The tag %#codegen must be included if you wish to generate code with 
% MATLAB Coder.

[numberOfStates, numberOfParticles] = size(particles);
    
% Time-propagate each particle
%
% Euler integration of continuous-time dynamics x'=f(x) with sample time dt
dt = 0.05; % [s] Sample time
for kk=1:numberOfParticles
    particles(:,kk) = particles(:,kk) + vdpStateFcnContinuous(particles(:,kk))*dt;
end

% Add Gaussian noise with variance 0.025 on each state variable
processNoise = 0.025*eye(numberOfStates);
particles = particles + processNoise * randn(size(particles));
end

function dxdt = vdpStateFcnContinuous(x)
%vdpStateFcnContinuous Evaluate the van der Pol ODEs for mu = 1
dxdt = [x(2); (1-x(1)^2)*x(2)-x(1)];
end

unscentedKalmanFilter と particleFilter では指定する状態遷移関数が異なります。アンセンテッドカルマンフィルターに使用した状態遷移関数は、一連の状態仮説ではなく、1 つの状態仮説の次のタイムステップへの伝播のみを記述するものです。また、プロセスノイズの分布は unscentedKalmanFilter の ProcessNoise プロパティでその共分散のみによって定義されます。粒子フィルターでは、場合によってはさらに多くの統計プロパティを定義する必要のある、任意の分布を考慮することが可能です。この任意の分布とそのパラメーターは、particleFilter に指定する状態遷移関数内で完全に定義されます。

particleFilter に指定する測定尤度関数も、次の 2 つのタスクを実行しなければなりません。1. 粒子からの測定仮説の計算。2. センサー測定値およびステップ 1 で計算した仮説からの各粒子の尤度の計算。

type vdpExamplePFMeasurementLikelihoodFcn

function likelihood = vdpExamplePFMeasurementLikelihoodFcn(particles,measurement)
% vdpExamplePFMeasurementLikelihoodFcn Example measurement likelihood function
%
% The measurement is the first state.
%
% likelihood = vdpParticleFilterMeasurementLikelihoodFcn(particles, measurement)
%
% Inputs:
%    particles - NumberOfStates-by-NumberOfParticles matrix that holds 
%                the particles
%
% Outputs:
%    likelihood - A vector with NumberOfParticles elements whose n-th
%                 element is the likelihood of the n-th particle
%
% See also extendedKalmanFilter, unscentedKalmanFilter

%   Copyright 2017 The MathWorks, Inc.

%#codegen

% The tag %#codegen must be included if you wish to generate code with 
% MATLAB Coder.

% Validate the sensor measurement
numberOfMeasurements = 1; % Expected number of measurements
validateattributes(measurement, {'double'}, {'vector', 'numel', numberOfMeasurements}, ...
    'vdpExamplePFMeasurementLikelihoodFcn', 'measurement');

% The measurement is first state. Get all measurement hypotheses from particles
predictedMeasurement = particles(1,:);

% Assume the ratio of the error between predicted and actual measurements
% follow a Gaussian distribution with zero mean, variance 0.2
mu = 0; % mean
sigma = 0.2 * eye(numberOfMeasurements); % variance

% Use multivariate Gaussian probability density function, calculate
% likelihood of each particle
numParticles = size(particles,2);
likelihood = zeros(numParticles,1);
C = det(2*pi*sigma) ^ (-0.5);
for kk=1:numParticles
    errorRatio = (predictedMeasurement(kk)-measurement)/predictedMeasurement(kk);
    v = errorRatio-mu;
    likelihood(kk) = C * exp(-0.5 * (v' / sigma * v) );
end
end

次にフィルターを構築し、平均 [2; 0] の周りに 0.01 の共分散をもつ 1000 個の粒子に初期化します。共分散が小さいのは、推定 [2; 0] の信頼度が高いためです。

pf = particleFilter(@vdpParticleFilterStateFcn,@vdpExamplePFMeasurementLikelihoodFcn);
initialize(pf, 1000, [2;0], 0.01*eye(2));

オプションで、状態推定法を選択します。これは particleFilter の StateEstimationMethod プロパティによって設定され、'mean' (既定の設定) または 'maxweight' の値をとることができます。StateEstimationMethod が 'mean' の場合、オブジェクトは状態推定値として Particles プロパティと Weights から粒子の加重平均を抽出します。'maxweight' は、Weights の最大重量の値を状態推定値として粒子 (状態仮説) を選択することに対応します。あるいは、オブジェクトの Particles プロパティと Weights プロパティにアクセスして、任意の手法を選択して状態推定値を抽出することもできます。

pf.StateEstimationMethod

ans = 
'mean'

particleFilter では、そのResamplingPolicy プロパティと ResamplingMethod プロパティを使用してさまざまなリサンプリングオプションを指定できます。この例はフィルターの既定の設定を使用します。リサンプリングの詳細については、particleFilter のドキュメンテーションを参照してください。

pf.ResamplingMethod

ans = 
'multinomial'

pf.ResamplingPolicy

ans = 
  particleResamplingPolicy with properties:

                TriggerMethod: 'ratio'
             SamplingInterval: 1
    MinEffectiveParticleRatio: 0.5000

推定ループを開始します。これは時間の経過とともにステップごとに取得される測定値を表します。

% Estimate
xCorrectedPF = zeros(size(xTrue));
for k=1:size(xTrue,1)
    % Use measurement y[k] to correct the particles for time k
    xCorrectedPF(k,:) = correct(pf,yMeas(k)); % Filter updates and stores Particles[k|k], Weights[k|k]
    % The result is x[k|k]: Estimate of states at time k, utilizing
    % measurements up to time k. This estimate is the mean of all particles
    % because StateEstimationMethod was 'mean'.
    %
    % Now, predict particles at next time step. These are utilized in the
    % next correct command
    predict(pf); % Filter updates and stores Particles[k+1|k]
end

粒子フィルターからの状態推定値をプロットします。

figure();
subplot(2,1,1);
plot(timeVector,xTrue(:,1),timeVector,xCorrectedPF(:,1),timeVector,yMeas(:));
legend('True','Particlte filter estimate','Measured')
ylim([-2.6 2.6]);
ylabel('x_1');
subplot(2,1,2);
plot(timeVector,xTrue(:,2),timeVector,xCorrectedPF(:,2));
ylim([-3 1.5]);
xlabel('Time [s]');
ylabel('x_2');

Figure contains 2 axes objects. Axes object 1 with ylabel x_1 contains 3 objects of type line. These objects represent True, Particlte filter estimate, Measured. Axes object 2 with xlabel Time [s], ylabel x_2 contains 2 objects of type line.