磁性流体ダンパーの非線形モデリング
この例は、磁性流体ダンパーの動的動作の非線形ブラックボックス モデリングを示しています。この例から、速度と減衰力の測定値を使用して、ダンパーの非線形 ARX および Hammerstein-Wiener モデルを作成する方法がわかります。
この例で使用したデータは、Dr. Akira Sano (Keio University、Japan) および Dr. Jiandong Wang (Peking University、China) から提供されています。データは、慶応大学のラボで行われた実験に基づきます。実験システムと関連資料の詳細については、以下の参考文献を参照してください。
J.Wang, A. Sano, T. Chen, and B. Huang. Identification of Hammerstein systems without explicit parameterization of nonlinearity. International Journal of Control, In press, 2008.DOI: 10.1080/00207170802382376.
実験の設定
磁気レオロジー (MR) 流体ダンパーは、汎アクティブ制御デバイスで、さまざまな動的構造の振動を緩和するために使用します。MR 流体は、その粘度がデバイスの入力電圧/電流に依存し、制御可能な減衰力を提供します。
このようなデバイスの動作を調査するため、MR ダンパーは、その一端を接地し、もう一端は振動を生成するシェーカー台に接続しました。ダンパーの電圧は 1.25 v に設定しました。減衰力 f(t) は 0.005 秒ごとにサンプリングしました。変位は、0.001 秒ごとにサンプリングし、サンプリング周期 0.005 秒で速度 v(t) の推定に使用しました。
入出力データ
入力および出力測定値を含むデータセットは、mrdamper.mat という名前の MAT ファイルに保存しました。入力 v(t) はダンパーの速度 [cm/s] で、出力は f(t) は減衰力 [N] です。MAT ファイルには、サンプリング レート 0.005 秒に対応する 3499 のサンプル データが含まれます。このデータは、この例で実行するすべての推定および検証作業に使用します。
% Let us begin by loading and inspecting the data. load('mrdamper.mat'); who
Your variables are: F Ts V
読み込んだ変数 F (出力の力)、V (入力速度) および Ts (サンプル時間) を IDDATA オブジェクトにパッケージ化します。
z = iddata(F, V, Ts, 'Name', 'MR damper', ... 'InputName', 'v', 'OutputName', 'f',... 'InputUnit', 'cm/s', 'OutputUnit', 'N');
推定と検証に使用するデータの準備
このデータセットを 2 つのサブセットに分割します。1 つは推定 (ze) に使用する 2000 サンプルを含み、もう 1 つは結果の検証 (zv) に使用する残りのデータです。
ze = z(1:2000); % estimation data zv = z(2001:end); % validation data
2 つのデータセットを合わせてプロットし、その時間範囲を目視により確認します。
plot(ze, zv) legend('ze','zv')

モデル次数の選択
ブラック ボックス モデルを推定する最初のステップは、モデル次数の選択です。次数の定義は、モデルのタイプに左右されます。
線形および非線形 ARX モデルの場合、次数は、na、nb および nk という 3 つの数値で表されます。これらの数値は、過去の出力数、過去の入力および入力遅延を定義し、与えられた時間の出力値を予測するときに使用されます。次数で定義した一連の時間遅延 I/O 変数を、"リグレッサー" と呼びます。より柔軟にリグレッサーを作成するために、リグレッサーの仕様オブジェクト (linearRegressor、polynomialRegressor、customRegressor を参照) を使用できます。
静的 I/O 非線形で線形モデルを表す Hammerstein-Wiener モデルの場合、次数は、極および零点数と線形成分の入力遅延を定義します。これらは、数値 nb (零点数 +1)、nf (極数)、および nk (ラグ数による入力遅延)で定義されます。
一般に、モデル次数は、試行錯誤により選択します。ただし、線形 ARX モデルの次数は、arxstruc や selstruc などの関数を使用して自動的に算出できます。こうして取得した次数は、非線形モデルで使用する次数を選択する際にも参考となります。まず、線形 ARX モデルの最適な次数を求めます。
V = arxstruc(ze,zv,struc(1:5, 1:5,1:5)); % try values in the range 1:5 for na, nb, nk Order = selstruc(V,'aic') % selection of orders by Akaike's Information Criterion
Order =
2 4 1
AIC 条件では、Order = [na nb nk] = [2 4 1] が選択されていますが、これは、選択した ARX モデル構造で、ダンパー力 f(t) が 6 つのリグレッサー f(t-1)、f(t-2)、v(t-1)、v(t-2)、v(t-3) および v(t-4) で予測されることを意味します。
モデル次数の選択についての詳細は、次の例を参照してください。「モデル構造の選択: モデル次数と入力遅延の決定」
予備解析: 線形モデルの作成
作成が容易であるため、まず線形モデルを試すことをお勧めします。線形モデルの結果が不十分である場合でも、その結果は、非線形モデルを展開する基盤となります。
前述の SELSTRUC で示された次数の線形 ARX および出力誤差 (OE) モデルを推定します。
LinMod1 = arx(ze, [2 4 1]); % ARX model Ay = Bu + e LinMod2 = oe(ze, [4 2 1]); % OE model y = B/F u + e
同様に、次数を自動的に求められる (= 状態数) 線形状態空間モデルを作成できます。
LinMod3 = ssest(ze); % creates a state-space model of order 3
次に、これらのモデルの応答を、ze の測定出力データと比較します。
compare(ze, LinMod1, LinMod2, LinMod3) % comparison to estimation data
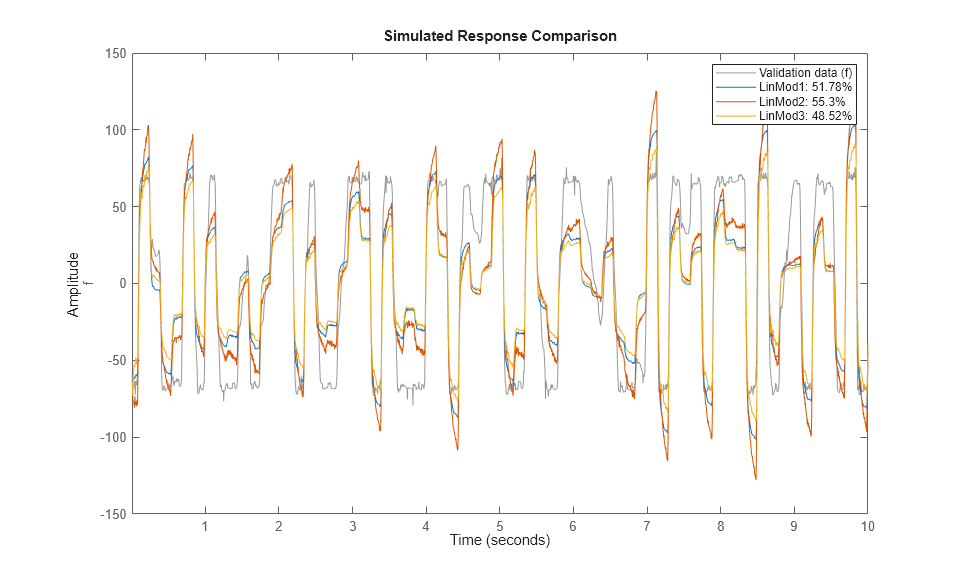
モデルの質の良好なテストは、各データセットに対して検証を行います。したがって、モデルの応答をデータセット zv と比較します。
compare(zv, LinMod1, LinMod2, LinMod3) % comparison to validation data
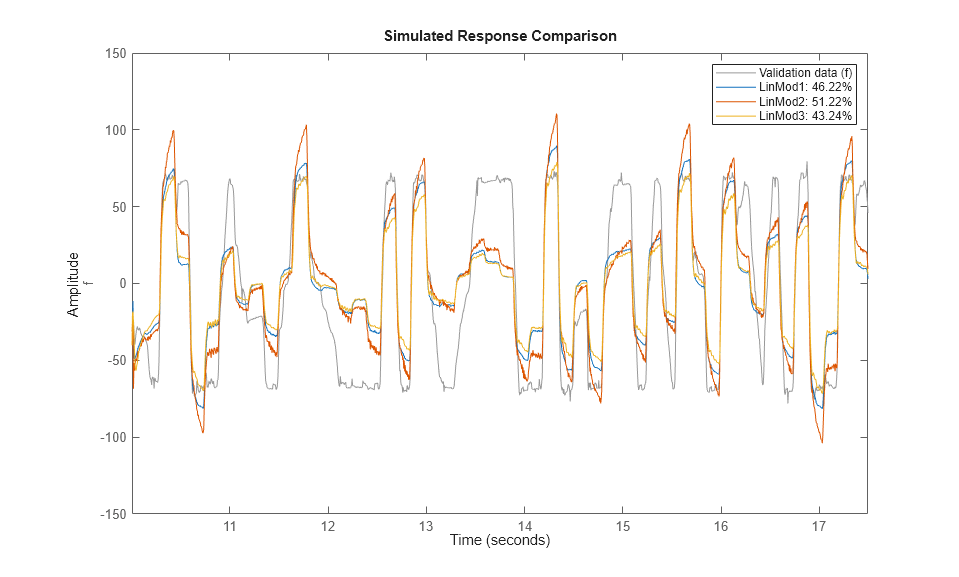
ご覧のように、最適な線形モデルは、検証データセットで 51% の適合となっています。
非線形 ARX モデルの作成
線形モデルの同定により、ARX モデルが検証データで 50% 未満の適合であることがわかります。結果を改善するため、非線形 ARX (IDNLARX) モデルを使用します。このデータで非線形モデルを使用する必要があることは、adviceユーティリティでも示されています。このユーティリティを使用すると、線形モデルに対して非線形モデルを使用する利点をデータで確認できます。
advice(ze, 'nonlinearity')
There is an indication of nonlinearity in the data. A nonlinear ARX model of order [4 4 1] and idTreePartition function performs better prediction of output than the corresponding ARX model of the same order. Consider using nonlinear models, such as IDNLARX, or IDNLHW. You may also use the "isnlarx" command to test for nonlinearity with more options.
非線形 ARX モデルは、ARX モデルの非線形バージョンで、2 つの意味でモデリングの優れた柔軟性が得られます。
リグレッサーは、ARX モデルで使用する加重合計ではなく、非線形関数を使用して結合できます。シグモイド ネットワーク、バイナリ ツリーおよびウェーブレット ネットワークなどの非線形関数を使用できます。同定のコンテキストでは、これらの関数を "非線形マッピング関数" と呼びます。
リグレッサー自体は、ARX モデルで使用する時間遅延変数値に加えて、I/O 変数の任意 (通常は非線形) 関数となります。
非線形 ARX モデル用リグレッサーの作成
連続しているラグをもつ線形の場合、リグレッサーは上記のように次数行列 [na nb nk] を使用して作成するのが最も簡単です。任意のラグをもつ最も一般的なリグレッサーの場合、またはリグレッサーが変数の絶対値に基づく場合、linearRegressor オブジェクトを使用すると柔軟性が向上します。リグレッサーが時間遅延変数の多項式である場合は、polynomialRegressor オブジェクトを使用して作成できます。任意のユーザー指定式を使用しているリグレッサーには、customRegressor オブジェクトを使用できます。
ここでは、複数のモデル次数と非線形マッピング関数を使用します。多項式またはカスタムのリグレッサーの使用は対象ではありません。IDNLARX モデルでカスタムのリグレッサーを指定する方法については、「非線形リグレッサーおよびカスタム リグレッサーを含む非線形 ARX モデルの作成」の例を参照してください。
既定の非線形 ARX モデルの推定
まず最初に、非線形タイプとして、次数 [24 1] の IDNLARX モデルとシグモイド ネットワークを推定します。MaxIterations = 50 と Levenberg-Marquardt 検索法を、以下すべての推定において推定オプションとして使用します。
Options = nlarxOptions('SearchMethod', 'lm'); Options.SearchOptions.MaxIterations = 50; Narx1 = nlarx(ze, [2 4 1], idSigmoidNetwork, Options)
Narx1 = <strong>Nonlinear ARX model with 1 output and 1 input</strong> Inputs: v Outputs: f Regressors: Linear regressors in variables f, v Output function: Sigmoid network with 10 units Sample time: 0.005 seconds Status: Estimated using NLARX on time domain data "MR damper". Fit to estimation data: 95.8% (prediction focus) FPE: 6.648, MSE: 6.08
nlarx は、非線形 ARX モデルを推定するためのコマンドです。Narx1 は、リグレッサー R := [f(t-1), f(t-2), v(t-1) ... v(t-4)] を含む非線形 ARX モデルです。非線形はシグモイド ネットワークで、シグモイド ユニット関数とリグレッサーの線形加重合計を組み合わせて使用し、出力を算出します。マッピング関数はモデルの OutputFcn プロパティに格納されます。
disp(Narx1.OutputFcn)
<strong>Sigmoid Network</strong>
Inputs: f(t-1), f(t-2), v(t-1), v(t-2), v(t-3), v(t-4)
Output: f(t)
Nonlinear Function: Sigmoid network with 10 units
Linear Function: initialized to [48.3 -3.38 -3.34 -2.7 -1.38 2.15]
Output Offset: initialized to -21.4
NonlinearFcn: '<Sigmoid units and their parameters>'
LinearFcn: '<Linear function parameters>'
Offset: '<Offset parameters>'
シミュレートした出力を推定データセット ze および検証データセット zv と比較して、モデルを確認します。
compare(ze, Narx1); % comparison to estimation data
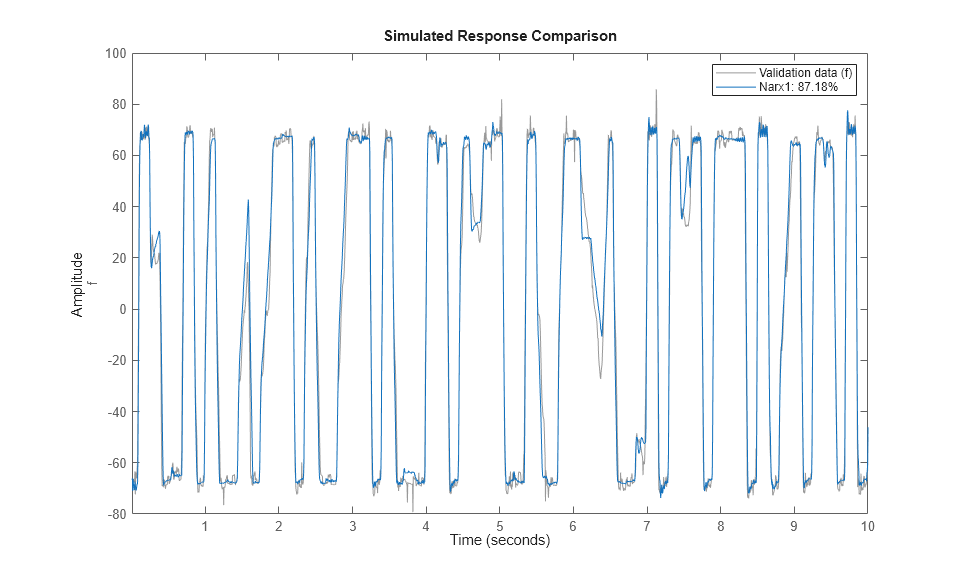
compare(zv, Narx1); % comparison to validation data
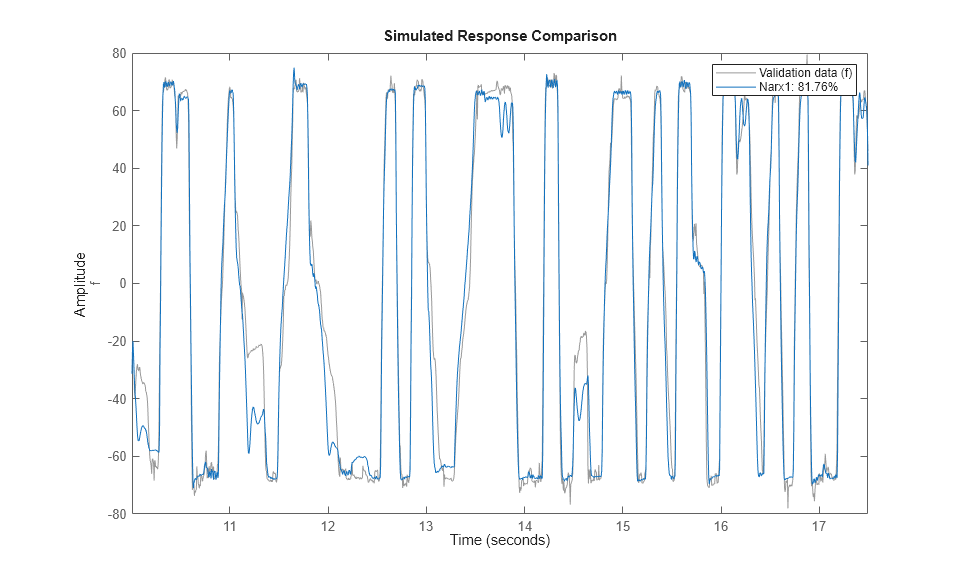
複数のモデル次数の試行
同じ次数の線形モデルよりも、良好な適合が見られます。次に、SELSTRUC で示された次数の周辺で別の次数を試します。
NL = idSigmoidNetwork;
Narx2{1} = nlarx(ze, [3 4 1], NL, Options); % use na = 3, nb = 4, nk = 1.
Narx2{1}.Name = 'Narx2_1';
Narx2{2} = nlarx(ze, [2 5 1], NL, Options); Narx2{2}.Name = 'Narx2_2';
Narx2{3} = nlarx(ze, [3 5 1], NL, Options); Narx2{3}.Name = 'Narx2_3';
Narx2{4} = nlarx(ze, [1 4 1], NL, Options); Narx2{4}.Name = 'Narx2_4';
Narx2{5} = nlarx(ze, [2 3 1], NL, Options); Narx2{5}.Name = 'Narx2_5';
Narx2{6} = nlarx(ze, [1 3 1], NL, Options); Narx2{6}.Name = 'Narx2_6';
推定および検証データセットで、これらのモデルのパフォーマンスを評価します。
compare(ze, Narx1, Narx2{:}); % comparison to estimation data

compare(zv, Narx1, Narx2{:}); % comparison to validation data
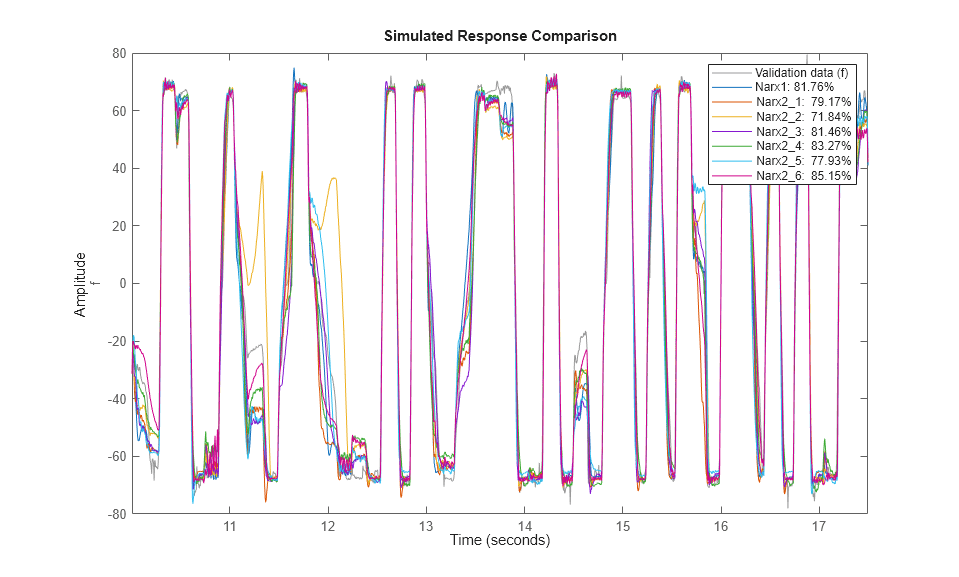
モデル Narx2{6} が、推定および検証データセットの両方で良好な適合を示していますが、その次数は、Narx1 よりも低くなっています。この結果に基づいて、後続の試行では次数 [1 3 1] を使用し、適合比較には Nlarx2{6} を維持します。この次数の選択は、一連のリグレッサーとして [f(t-1), v(t-1), v(t-2), v(t-3)] の使用に対応します。
シグモイド ネットワーク関数のユニット数の指定
次に、シグモイド ネットワーク関数の構造を検討します。この推定器の一番妥当なプロパティは、使用するシグモイド ユニット数です。12 個のシグモイド ユニットを使用するシグモイド ネットワークを作成します。
Sig = idSigmoidNetwork(12); % create a network that uses 12 units
Narx3 = nlarx(ze, [1 3 1], Sig, Options);
このモデルを、推定および検証データセットで、Narx1 および Narx2{6} と比較します。
compare(ze, Narx3, Narx1, Narx2{6}); % comparison to estimation data
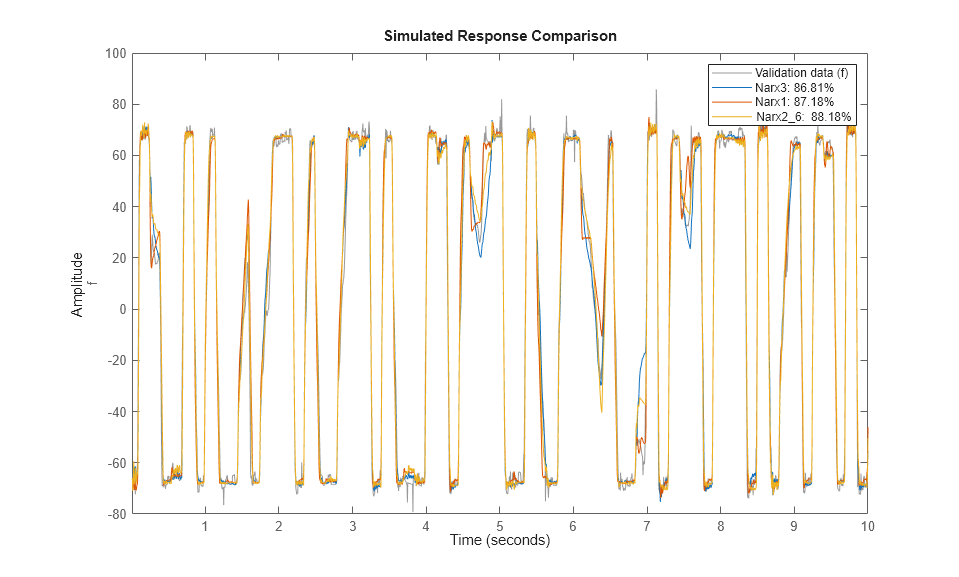
compare(zv, Narx3, Narx1, Narx2{6}); % comparison to validation data
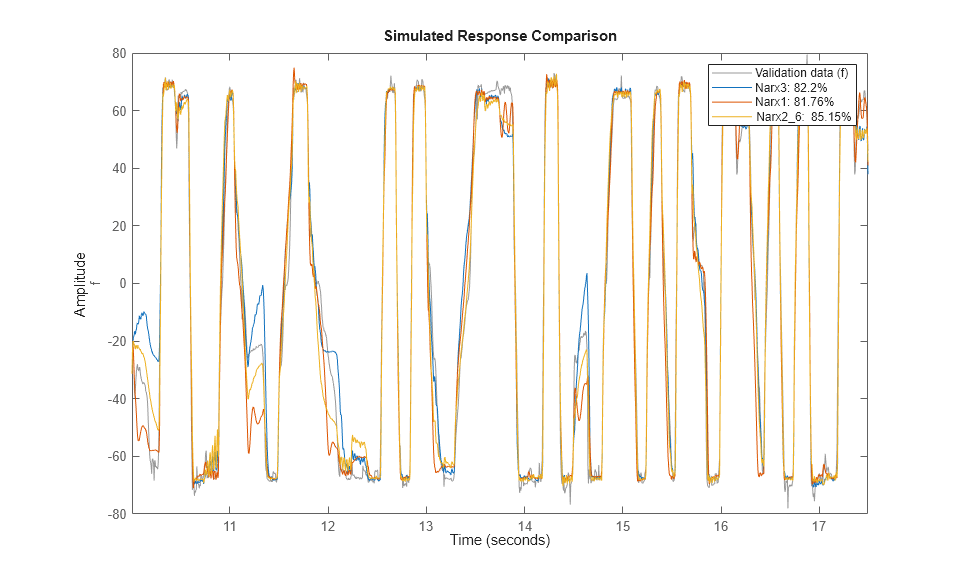
新規モデル Narx3 では、Narx2{6} より優れた適合は得られません。したがって、後続の試行でもユニット数 10 を保持します。
非線形マッピング関数のリグレッサーのサブセットの選択
一般に、選択した次数 (ここでは [1 3 1]) で定義されるすべてのリグレッサーが、非線形関数 (シグモイド ネットワーク) で使用されます。リグレッサーの数が多いと、モデルが複雑になる場合があります。モデル次数を変更せずに、シグモイド ネットワークのコンポーネントが使用するリグレッサーのサブセットを選択できます。これは 'RegressorUsage' という名前のプロパティを使用すると簡単です。その値は、どのリグレッサーがどのコンポーネントに使用されるかを指定する table です。たとえば、シグモイド関数の非線形コンポーネントで使用する入力変数に関連するリグレッサーだけを使用するように調整できます。以下のように実行できます。
Sig = idSigmoidNetwork(10);
NarxInit = idnlarx(ze.OutputName, ze.InputName, [1 3 1], Sig);
NarxInit.RegressorUsage.("f:NonlinearFcn")(1) = false;
disp(NarxInit.RegressorUsage)
Narx4 = nlarx(ze, NarxInit, Options);
f:LinearFcn f:NonlinearFcn
___________ ______________
f(t-1) true false
v(t-1) true true
v(t-2) true true
v(t-3) true true
これで、リグレッサー (t-1)、v(t-2)、および v(t-3) がシグモイド ユニット関数で使用されるようになります。出力変数に基づいたリグレッサー f(t-1) は使用しません。関数 idSigmoidNetwork は、すべてのリグレッサーの加重合計による線形項も含みます。線形条件は、リグレッサーのフル セットを使用します。
非線形コンポーネントにリグレッサー {y1(t-1), u1(t-2), u1(t-3)} を使用する別のモデルを作成します。
Use = false(4,1);
Use([1 3 4]) = true;
NarxInit.RegressorUsage{:,2} = Use;
Narx5 = nlarx(ze, NarxInit, Options);
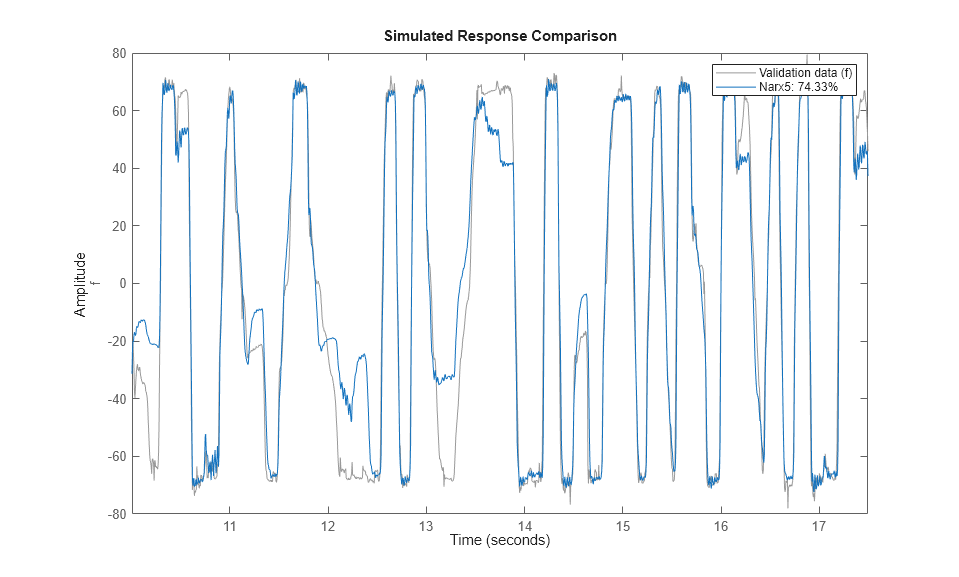
モデル Narx5 は、推定データセットと検証データセットの両方で非常に良好であることがわかります。
compare(ze, Narx5); % comparison to estimation data
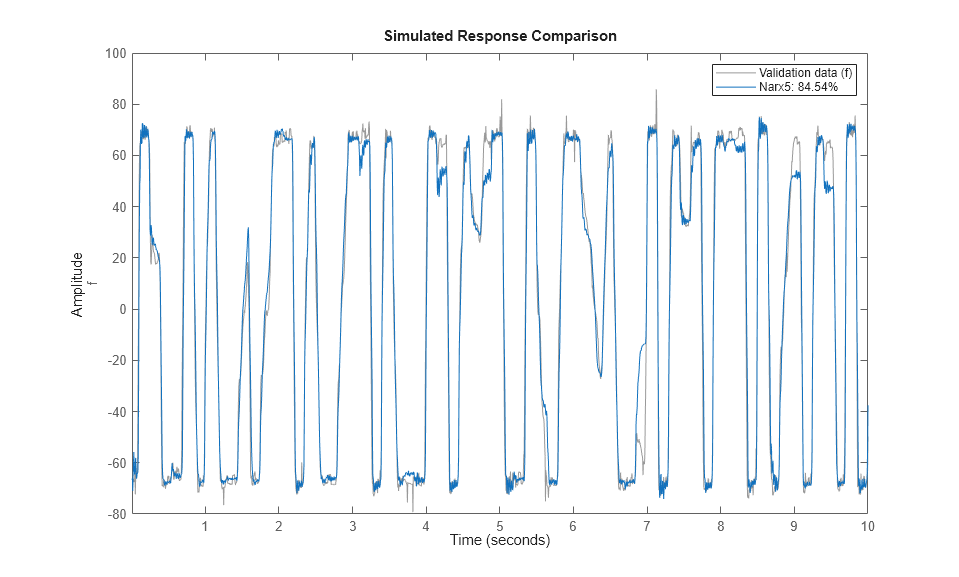
compare(zv, Narx5); % comparison to validation data
複数の非線形マッピング関数の試行
ここまで、複数のモデル次数、シグモイド ネットワーク関数で使用するユニット数、およびシグモイド ネットワークの非線形コンポーネントで使用するリグレッサーのサブセットの指定について評価してきました。次に、別のタイプの非線形関数を使用してみます。
ウェーブレット ネットワーク関数は、既定のプロパティで使用します。シグモイド ネットワークと同様に、ウェーブレット ネットワークは線形コンポーネントと非線形コンポーネントの和を使用して、リグレッサーを出力にマッピングします。非線形コンポーネントはウェーブレットの和を使用します。
NarxInit = idnlarx(ze.OutputName, ze.InputName, [1 3 1], idWaveletNetwork); % Use only regressors 1 and 3 for the nonlinear component of network NarxInit.RegressorUsage.("f:NonlinearFcn")([2 4]) = false; Narx6 = nlarx(ze, NarxInit, Options);
ツリー パーティション非線形関数は 20 ユニットで使用します。
TreeNet = idTreePartition; TreeNet.NonlinearFcn.NumberOfUnits = 20; NarxInit.OutputFcn = TreeNet; Narx7 = nlarx(ze, NarxInit, Options);
結果を Narx3 および Narx5 と比較します。
compare(ze, Narx3, Narx5, Narx6, Narx7) % comparison to estimation data
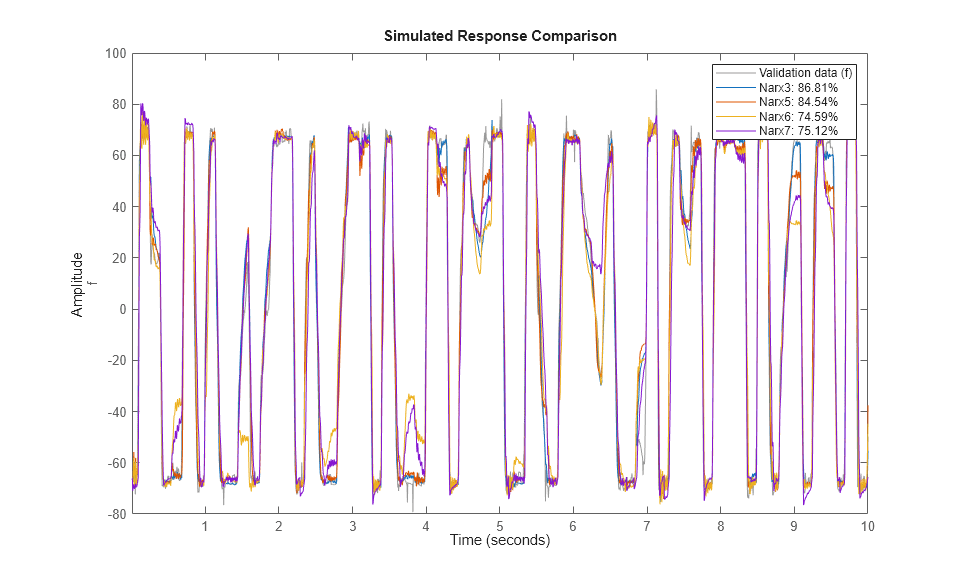
compare(zv, Narx3, Narx5, Narx6, Narx7) % comparison to validation data
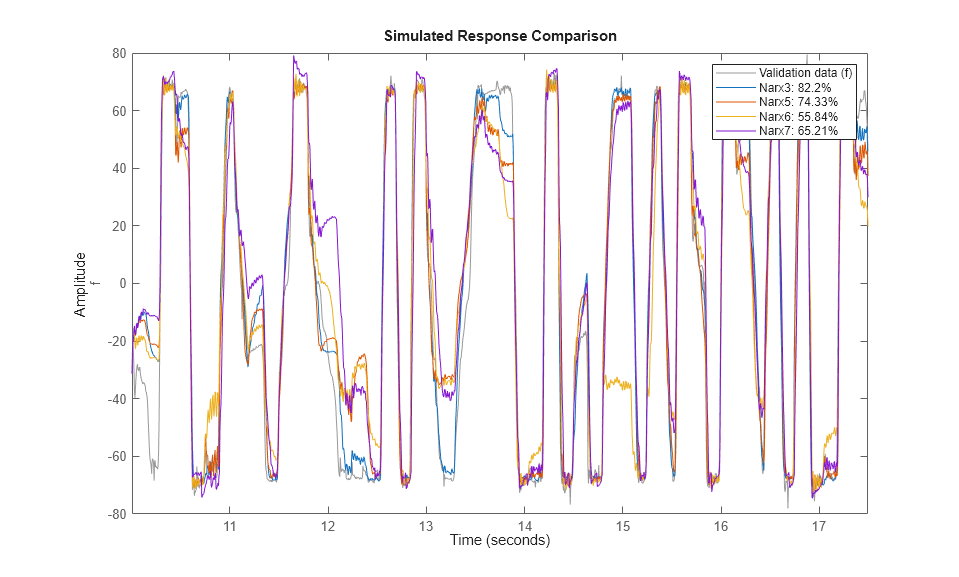
モデル Narx6 および Narx7 は、Narx5 よりも結果が良くないように見えますが、この推定に関連するすべてのオプションをテストしてはいません (非線形リグレッサー、ユニット数および他のモデル次数の選択など)。
推定した IDNLARX モデルの解析
compare コマンドを使用して、モデルを同定し、検証したら、あまり複雑度が高くならないように、最適な結果が得られるモデルを仮に選択できます。選択したモデルは plot や resid などのコマンドを使用して、さらに解析できます。
モデルの非線形特性について詳しい情報を得るため、推定モデル (t) = F(f(t-1), f(t-2), v(t-1),...,v(t-4)) の非線形関数 F() の断面を確認します。たとえば、モデル Narx5 では、関数 F() がシグモイド ネットワークです。F() の出力の形状をリグレッサーの関数として評価するため、モデルで plot コマンドを使用します。
plot(Narx5)

プロット ウィンドウには、断面リグレッサーとその範囲を選択するツールがあります。詳細については、"help idnlarx/plot" を参照してください。
残差テストを使用すると、モデルをさらに確認できます。このテストにより、予測誤差がホワイトで、入力データと相関しないことがわかります。
set(gcf,'DefaultAxesTitleFontSizeMultiplier',1,... 'DefaultAxesTitleFontWeight','normal',... 'Position',[100 100 780 520]); resid(zv, Narx3, Narx5)

残差テストが失敗した場合、モデルでダイナミクスが捕捉されていないと考えられます。モデル Narx3 の場合、残差はほぼ 99% の信頼限界内に入っています。
Hammerstein-Wiener モデルの作成
これまでに推定した非線形モデルは、すべて非線形 ARX (IDNLARX) タイプでした。Hammerstein-Wiener (IDNLHW) モデルを実行します。これらのモデルは、線形モデルの静的非線形要素をつなぎ合わせたものとなります。これらは、線形出力誤差 (OE) モデルの延長と考えることができますが、線形モデルの入出力信号は、飽和または不感帯など、静的非線形の対象とします。
同じ次数の IDNLHW モデルの線形 OE モデルとしての推定
線形 OE モデルl LinMod2 は、次数 nb = 4、nf = 2、および nk = 1 を使用して推定しました。ここでは、同じ次数を使って IDNLHW モデルを推定します。シグモイド ネットワークを、入力および出力非線形の非線形性として使用します。推定には、nlhw コマンドを使用すると便利です。これは、線形 OE モデルの推定に使用する oe コマンドに相当します。ただし、モデル次数だけでなく、I/O 非線形の名前またはオブジェクトも指定します。
Opt = nlhwOptions('SearchMethod','lm'); UNL = idSigmoidNetwork; YNL = idSigmoidNetwork; Nhw1 = nlhw(ze, [4 2 1], UNL, YNL, Opt)
Nhw1 = <strong>Hammerstein-Wiener model with 1 output and 1 input</strong> Linear transfer function corresponding to the orders nb = 4, nf = 2, nk = 1 Input nonlinearity: Sigmoid network with 10 units Output nonlinearity: Sigmoid network with 10 units Sample time: 0.005 seconds Status: Estimated using NLHW on time domain data "MR damper". Fit to estimation data: 83.98% FPE: 94.65, MSE: 88.34
このモデルの応答を、推定および検証データセットと比較します。
clf
compare(ze, Nhw1); % comparison to estimation data

compare(zv, Nhw1); % comparison to validation data
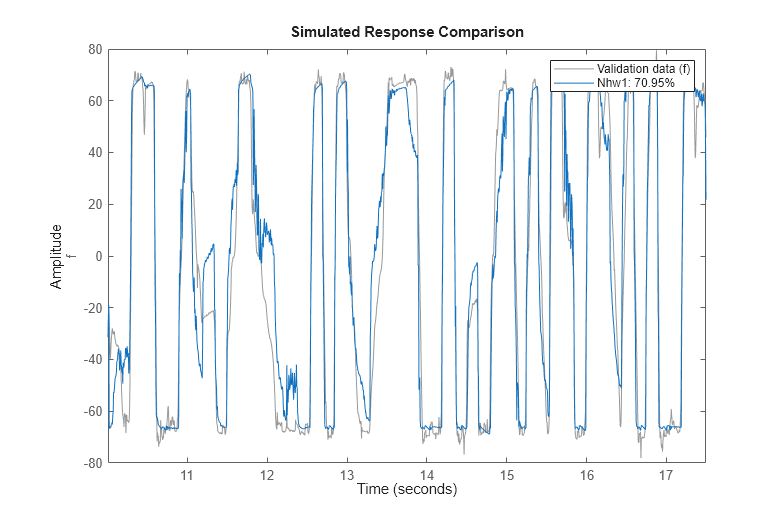
モデル Nhw1 を使用すると、検証データに約 70% の適合が得られます。
推定した IDNLHW モデルの解析
非線形 ARX モデルの場合、Hammerstein-Wiener モデルで、PLOT コマンドを使用して、I/O 非線形の特性と非線形成分の動作を評価できます。詳細については、MATLAB® コマンド ウィンドウで "help idnlhw/plot" を入力します。
plot(Nhw1)
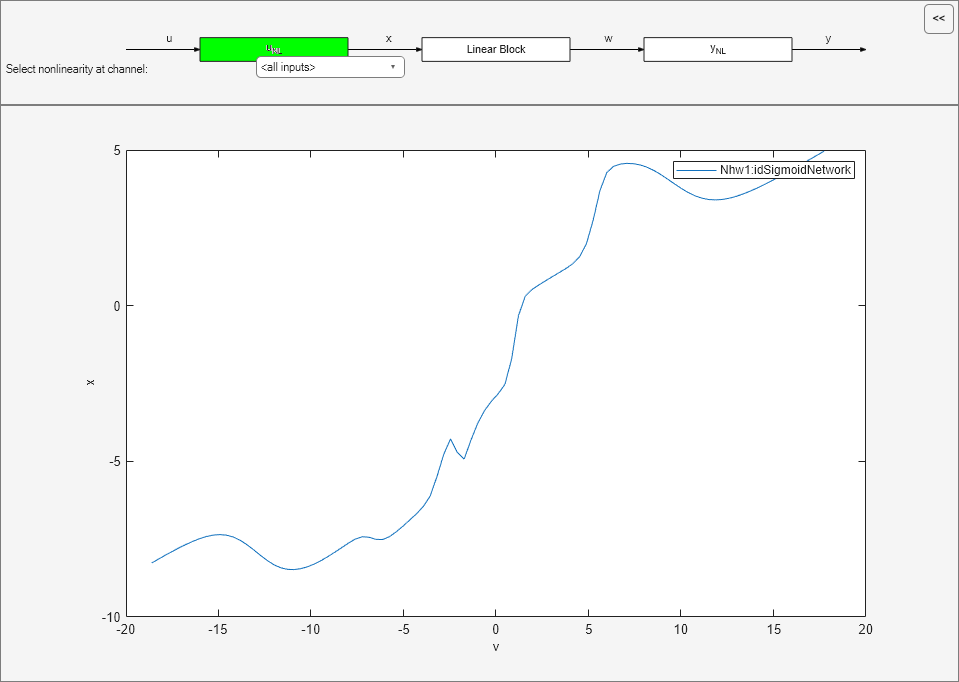
既定の設定では、入力非線形がプロットされ、飽和関数であることがわかります。
Y_NL アイコンをクリックすると、出力非線形が、区分的線形関数のように表示されます。
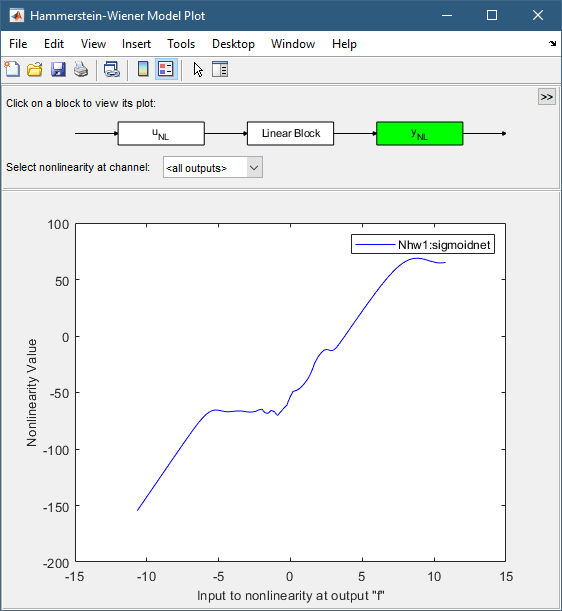
[Linear Block] アイコンをクリックし、プルダウン メニューから [Pole-Zero Map] を選択すると、零点と極がお互いに近接していることが確認できるため、これらを削除し、モデル次数を減らせることがわかります。

この情報を使用して、次に示したモデルの構造を設定します。
複数の非線形関数とモデル次数の試行
入力非線形には飽和を、出力非線形にはシグモイド ネットワークを使用し、線形成分の次数を維持します。
Nhw2 = nlhw(ze, [4 2 1], idSaturation, idSigmoidNetwork, Opt);
出力には区分的線形の非線形を、入力にはシグモイド ネットワークを使用します。
Nhw3 = nlhw(ze, [4 2 1], idSigmoidNetwork, idPiecewiseLinear, Opt);
低次数の線形モデルを使用します。
Nhw4 = nlhw(ze, [3 1 1], idSigmoidNetwork, idPiecewiseLinear, Opt);
また、入力、出力または両方で非線形の "削除" を選択することもできます。たとえば、入力非線形だけを使用するには (このようなモデルは Hammerstein モデルと呼ばれます)、出力非線形を指定できます。
Nhw5 = nlhw(ze, [3 1 1],idSigmoidNetwork, [], Opt);
すべてのモデルを比較します。
compare(ze, Nhw1, Nhw2, Nhw3, Nhw4, Nhw5) % comparison to estimation data
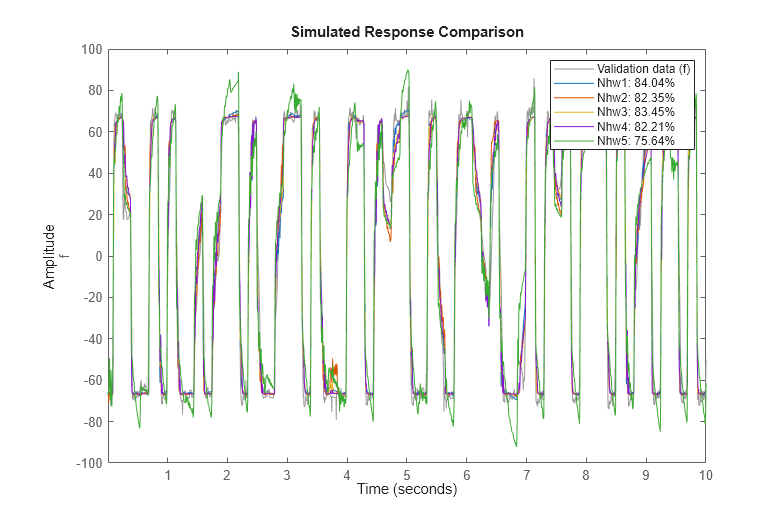
compare(zv, Nhw1, Nhw2, Nhw3, Nhw4, Nhw5) % comparison to validation data
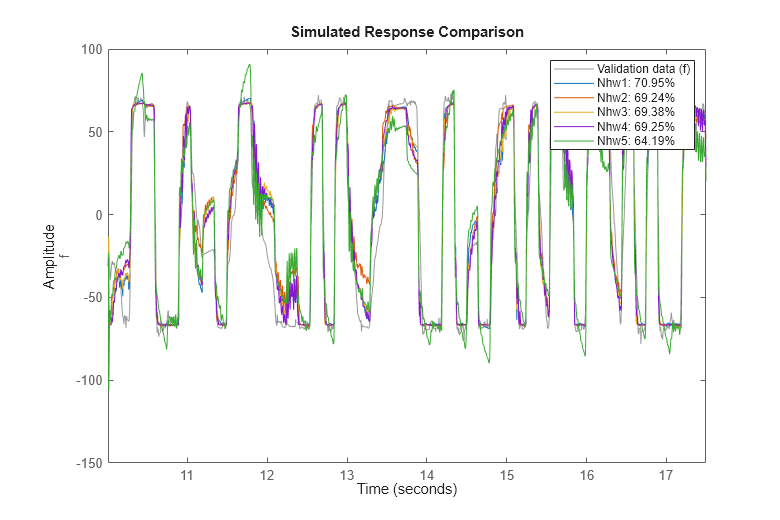
Nhw1 は、検証データとの比較でわかるように、すべてのモデル中で最良の結果を示していますが、Nhw5 を除く他のモデルは、同様のパフォーマンスとなっています。
まとめ
ここでは、さまざまな非線形モデルを使用して、電圧入力と減衰力出力の関係を説明してきました。非線形 ARX モデルの中では Narx2{6} および Narx5 が最良で、Hammerstein-Wiener モデルではモデル Nhw1 が最良であることが判明しました。また、MR ダンパーのダイナミクスを記述するには、非線形 ARX モデルが最適なオプション (最適適合) であることもわかりました。
Narx5.Name = 'Narx5'; Nhw1.Name = 'Nhw1'; compare(zv, LinMod2, Narx2{6}, Narx5, Nhw1)

結果の質を微調整するために、各モデルのタイプで複数のオプションが利用できることもわかりました。非線形 ARX モデルの場合、モデル次数と非線形関数のタイプを指定できるだけでなく、リグレッサーの使い方を設定し、選択した関数のプロパティを調整することもできます。Hammerstein-Wiener モデルの場合、入力および出力非線形関数のタイプと、線形成分の次数を選択できます。どちらのモデル タイプの場合も、自由に試行し、使用できる非線形関数にはさまざまな選択肢があります。モデル構造に特定の優先度がない場合、または基本ダイナミクスの知識がない場合、複数の選択肢を試行し、得られるモデルの質に対する効果を解析することをお勧めします。