このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。
モーター付きカメラ - 多入力/多出力非線形 ARX および Hammerstein-Wiener モデル
この例では、多入力/多出力 (MIMO) 非線形ブラック ボックス モデルをデータから推定する方法を説明します。System Identification Toolbox™ では、非線形 ARX モデルと Hammerstein-Wiener モデルという 2 種類の非線形ブラック ボックス モデルが利用できます。
測定するデータセット
この例では、ファイル motorizedcamera.mat に保存されているデータを使用します。このファイルには、モーター付きカメラからサンプル時間 0.02 秒で収集した 188 のデータ サンプルが含まれています。入力ベクトル u(t) は 6 つの変数で構成されます。これらの変数とは、カメラに固定された直交 X-Y-Z 座標系の 3 つの並進速度成分 [m/s] と、X-Y-Z 軸周りの 3 つの回転速度成分 [rad/s] です。出力ベクトル y(t) は 2 つの変数を含みます。これらの変数は、3D 空間の固定カメラ ポイントから取得したイメージによるポイントの位置 (ピクセル単位) です。IDDATA オブジェクト z を作成し、ロードしたデータを保持します。

load motorizedcamera z = iddata(y, u, 0.02, 'Name', 'Motorized Camera', 'TimeUnit', 's');
非線形 ARX (IDNLARX) モデル - リグレッサーの選択
まず最初に、非線形 ARX モデルを実行します。2 つの重要な要素を選択する必要があります。それは、モデルリグレッサーと非線形マッピング関数です。
リグレッサーは時間遅延 I/O 変数に基づいた単純な式であり、その最も簡単なケースは連続値の小さなセットによって遅延した変数です。たとえば、入力変数の名前が "u"、出力変数の名前が "y" の場合、リグレッサー セットの例は { y(t-1), y(t-2), u(t), u(t-1), u(t-2) } になります。ここで "t" は時間変数を表します。多項式の項を含むもう 1 つの例は、{y(t-2)^4, y(t-2)*u(t-1), u(t-4)^2} になります。遅延変数には、より複雑な任意の式も可能です。
線形リグレッサーを指定する最も簡単な方法は、"次数行列" を使う方法です。この行列は NN = [na nb nk] という形式をとり、各出力変数 (na) および各入力変数 (nb, nk) を何個のラグで遅延させるかを指定します。これは、線形 ARX モデル (ARX、IDPOLY を参照) の推定時に使用した考え方と同じです。たとえば NN = [2 3 4] は、リグレッサー セット {y(t-2), u(t-4), u(t-5), u(t-6)} を意味します。NY 個の出力と NU 個の入力があるモデルの一般的なケースでは、NN は NY 行および NY+2*NU 行の行列となります。
非線形 ARX (IDNLARX) モデル - ウェーブレット ネットワークを使用した予備推定
まず、次数 NN = [na nb nk] = [ones(2,2), ones(2,6), ones(2,6)] を選択します。これは、各出力変数が、出力および入力変数によって予測され、それぞれが 1 サンプルずつ遅延されることを意味します。モデル方程式は、y_i(t) = F_i(y1(t-1), y2(t-1), u1(t-1), u2(t-1), u3(t-1)), i = 1, 2 のように記述できます。ウェーブレット ネットワーク (idWaveletNetwork オブジェクト) を両方の出力に対する非線形マッピング関数として選択します。関数 NLARX は非線形 ARX モデルのパラメーターを推定します。
NN = [ones(2,2), ones(2,6), ones(2,6)]; % the orders
mw1 = nlarx(z, NN, idWaveletNetwork);
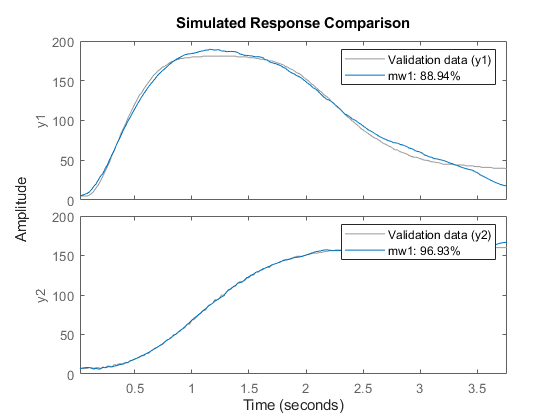
推定モデルでシミュレートした出力と、測定データ z の出力を比較して、結果を確認します。
compare(z,mw1)
非線形 ARX モデル - 高い次数を試行
高次数でも、良好な結果が得られるかどうかを確認します。モデルを同定する際に基底関数の拡張を使用して非線形性を表現する場合、モデル パラメーターの数がデータ サンプルの数を超える場合があることに注意してください。このような場合、ノイズ分散や最終予測誤差 (FPE) などの一部の推定メトリクスは正確に決定できません。現在の例では、この制限を知らせる警告をオフにします。
ws = warning('off','Ident:estimation:NparGTNsamp'); % mw2 = nlarx(z, [ones(2,2), 2*ones(2,6), ones(2,6)], idWaveletNetwork) compare(z,mw2)
mw2 = <strong>Nonlinear ARX model with 2 outputs and 6 inputs</strong> Inputs: u1, u2, u3, u4, u5, u6 Outputs: y1, y2 Regressors: Linear regressors in variables y1, y2, u1, u2, u3, u4, u5, u6 Output functions: Output 1: Wavelet network with 27 units Output 2: Wavelet network with 25 units Sample time: 0.02 seconds Status: Estimated using NLARX on time domain data "Motorized Camera". Fit to estimation data: [99.22;99.15]% (prediction focus) FPE: 0.1262, MSE: 0.4453
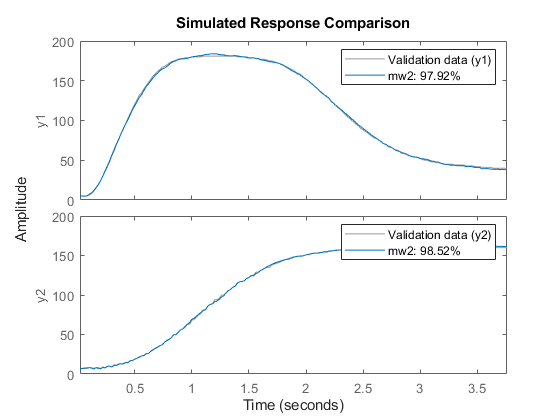
2 番目のモデル mw2 はかなり良好です。したがって、以下の例でも、このモデル次数の選択を使用します。
nanbnk = [ones(2,2), 2*ones(2,6), ones(2,6)]; % final orders
この次数の選択によって指定されるリグレッサー セットを表示するには、GETREG コマンドを使用します。
getreg(mw2)
ans =
14x1 cell array
{'y1(t-1)'}
{'y2(t-1)'}
{'u1(t-1)'}
{'u1(t-2)'}
{'u2(t-1)'}
{'u2(t-2)'}
{'u3(t-1)'}
{'u3(t-2)'}
{'u4(t-1)'}
{'u4(t-2)'}
{'u5(t-1)'}
{'u5(t-2)'}
{'u6(t-1)'}
{'u6(t-2)'}
2 つの関数 idWaveletNetwork のユニット数 ("wavelets") は、推定アルゴリズムで自動的に選択されています。これらの数値を以下に示します。
mw2.OutputFcn(1).NonlinearFcn.NumberOfUnits mw2.OutputFcn(2).NonlinearFcn.NumberOfUnits
ans =
27
ans =
25
非線形 ARX モデル - 非線形関数のユニット数を調整
関数 idWaveletNetwork のユニット数は、推定アルゴリズムで自動的に選択される代わりに、明示的に指定できます。1 番目の非線形マッピング関数に 10 個のユニットを、2 番目の非線形マッピング関数に 5 個のユニットを使用するとします。各出力のモデルは独自のマッピング関数を使用することと、すべてのマッピング関数の配列はモデルの "OutputFcn" プロパティに保存されていることに注意してください。
Fcn1 = idWaveletNetwork(10); % output function for the first output Fcn2 = idWaveletNetwork(5); % output function for the second output mw3 = nlarx(z, nanbnk, [Fcn1; Fcn2])
mw3 = <strong>Nonlinear ARX model with 2 outputs and 6 inputs</strong> Inputs: u1, u2, u3, u4, u5, u6 Outputs: y1, y2 Regressors: Linear regressors in variables y1, y2, u1, u2, u3, u4, u5, u6 Output functions: Output 1: Wavelet network with 10 units Output 2: Wavelet network with 5 units Sample time: 0.02 seconds Status: Estimated using NLARX on time domain data "Motorized Camera". Fit to estimation data: [99.01;98.89]% (prediction focus) FPE: 0.2273, MSE: 0.7443
非線形 ARX モデル - 他の非線形マッピング関数を試行
関数 idWaveletNetwork の代わりに、他の非線形関数も使用できます。両出力に対して idTreePartition を使用してみましょう。
mt1 = nlarx(z, nanbnk, idTreePartition);
上記の呼び出しでは、既定の構成のツリー パーティション マッピング関数が両出力に使用されています。
同様に、シグモイド ネットワーク (idSigmoidNetwork オブジェクト) をマッピング関数として使用できます。最大反復 (MaxIterations) や反復表示などの推定オプションは、nlarxOptions コマンドを使用して指定できます。
opt = nlarxOptions('Display','on'); opt.SearchOptions.MaxIterations = 5; ms1 = nlarx(z, nanbnk, idSigmoidNetwork, opt);
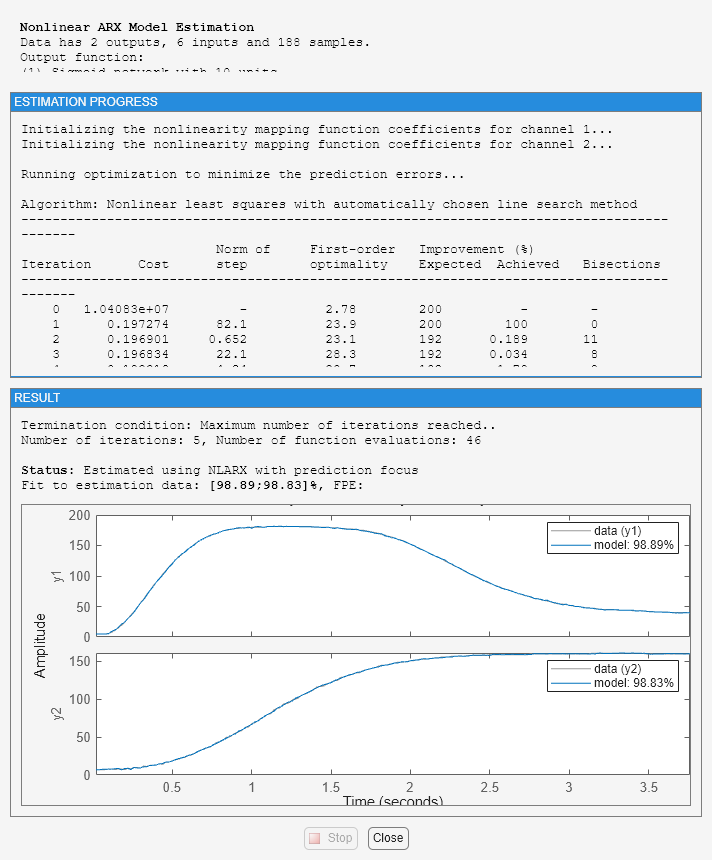
この NLARX の呼び出し構文は、以前使用した構文 (データ、次数、および非線形マッピング関数を基本入力引数として指定) とよく似ています。ただし、推定オプションを既定値から変更するために、nlarxOptions コマンドを使用してオプション セット opt を構成し、NLARX コマンドに追加の入力引数として渡しています。
各種の非線形関数を含む非線形 ARX モデル
同じモデルで、異なる出力チャネルに異なる非線形関数を使用できます。最初の出力の記述にはツリー パーティション関数を使用し、2 番目の出力には、ウェーブレット ネットワークを使用するとします。モデルの予測を以下に示します。3 番目の入力引数 (非線形マッピング関数) は、2 つの異なる関数の配列となります。
Fcn1 = idTreePartition; Fcn2 = idWaveletNetwork; mtw = nlarx(z, nanbnk, [Fcn1; Fcn2]);
場合によっては、リグレッサーをモデル出力にマッピングする関数を非線形にする必要はありません。この関数は単に、リグレッサー ベクトルの加重合計にオプションのオフセットを加えたものにできます。これは、線形 ARX モデルと類似 (オフセット項を除く) しています。出力チャネルに非線形が存在しないことは、関数 idLinear を選択すると指定できます。以下の例は、model_output(t) = F(y(t-1), u(t-1), u(t-2)) において、関数 F は 1 番目の出力に対して線形成分で、2 番目の出力に対して非線形成分 (idSigmoidNetwork) で構成されることを意味します。
Fcn1 = idLinear; Fcn2 = idSigmoidNetwork(2); opt.Display = 'off'; % do not show estimation progress anymore mls = nlarx(z, nanbnk, [Fcn1; Fcn2], opt)
mls = <strong>Nonlinear ARX model with 2 outputs and 6 inputs</strong> Inputs: u1, u2, u3, u4, u5, u6 Outputs: y1, y2 Regressors: Linear regressors in variables y1, y2, u1, u2, u3, u4, u5, u6 Output functions: Output 1: Linear with offset Output 2: Sigmoid network with 2 units Sample time: 0.02 seconds Status: Estimated using NLARX on time domain data "Motorized Camera". Fit to estimation data: [98.72;98.8]% (prediction focus) FPE: 0.5481, MSE: 1.041
1 番目の出力のモデルに非線形性はありません。ただし、オフセット項が存在するため、純線形ではありません。
disp(mls.OutputFcn(1))
<strong>Linear Function</strong>
Inputs: y1(t-1), y2(t-1), u1(t-1), u1(t-2), u2(t-1), u2(t-2), u3(t-1), u3(t-2), u4(t-1), u4(t-2), u5(t-1), u5(t-2), u6(t-1), u6(t-2)
Output: y1(t)
Linear Function: initialized to [48.3 -32.2 -0.229 -0.0706 -0.113 -0.0516 -0.182 0.297 0.199 -0.133 -0.337 0.583 -0.448 0.167]
Output Offset: initialized to -9.03e-06
LinearFcn: '<Linear function parameters>'
Offset: '<Offset parameters>'
オフセット項を使用しないように選択して、純線形にするオプションがあります。これは、推定する前にオフセットをゼロ値に固定することで選択できます。
Fcn1.Offset.Value = 0; Fcn1.Offset.Free = false; mlsNoOffset = nlarx(z, nanbnk, [Fcn1; Fcn2], opt);
Statistics and Machine Learning Toolbox の回帰アルゴリズムの使用
Statistics and Machine Learning Toolbox™ にアクセスできる場合、ガウス過程 (GP) 関数および、バギング木またはブースティング木のアンサンブルを使用しても、非線形 ARX モデルを作成できます。GP は idGaussianProcess オブジェクトで表されるのに対して、回帰木アンサンブルは idTreeEnsemble オブジェクトで表されます。GP は既定では二乗指数カーネルを使用します。他のカーネル タイプは、オブジェクト作成時に指定できます。ここに示す例では、1 番目の出力に 'ARDMatern52' カーネル ベースの GP を、2 番目の出力にバギング木アンサンブルを使用します。
if exist('fitrgp','file')==2 warning('off','stats:lasso:MaxIterReached'); NL1 = idGaussianProcess('ardmatern52'); NL2 = idTreeEnsemble; % estimate model mML = nlarx(z, nanbnk, [NL1; NL2]) end
mML = <strong>Nonlinear ARX model with 2 outputs and 6 inputs</strong> Inputs: u1, u2, u3, u4, u5, u6 Outputs: y1, y2 Regressors: Linear regressors in variables y1, y2, u1, u2, u3, u4, u5, u6 Output functions: Output 1: Gaussian process function using a ARDMatern52 kernel Output 2: Bagged Regression Tree Ensemble Sample time: 0.02 seconds Status: Estimated using NLARX on time domain data "Motorized Camera". Fit to estimation data: [99.29;98.44]% (prediction focus) MSE: 0.968
推定結果の確認
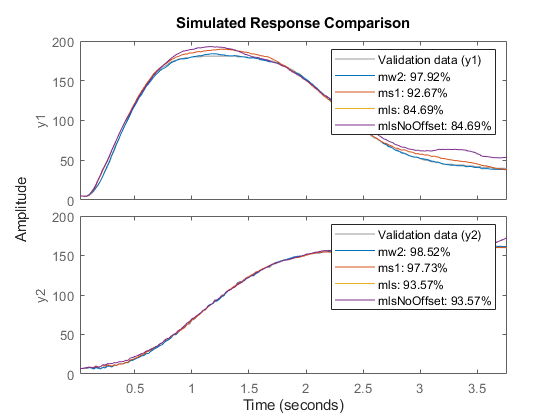
さまざまなモデルを、同じ COMPARE コマンドで比較できます。たとえば、モデル mw2、ms1、mls および mlsNoOffset のシミュレーション出力と、データセット "z" の測定された出力を比較します。
compare(z, mw2, ms1, mls, mlsNoOffset)
関数 plot を使用して、各モデルの非線形マッピング関数の "形状" を表示できます。
plot(mt1,mtw,ms1,mls)
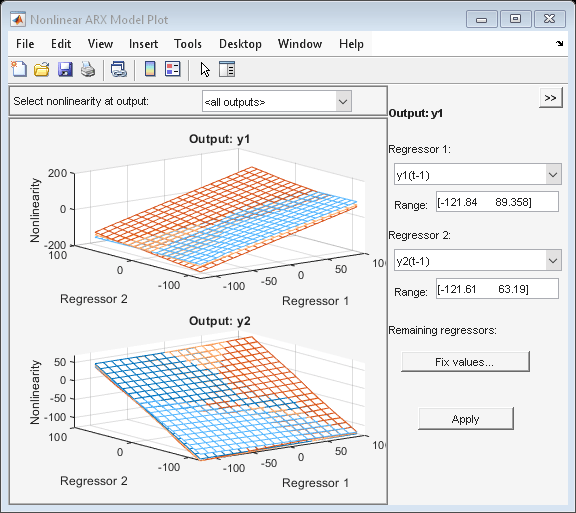
プロット右側にあるコントロール パネルで、リグレッサーを選択し、設定できます。
resid、predict、pe などの他の関数を、線形モデルの場合と同じように推定モデルで使用できます。
Hammerstein-Wiener (IDNLHW) モデル - 予備推定
Hammerstein-Wiener モデルは、最大 3 つのブロックで構成されます。これらのブロックとは、非線形静的ブロック、その後に続く別の非線形静的ブロック、さらにその後に続く線形伝達関数ブロックです。最初の非線形静的ブロックがない場合、Wiener モデルと呼ばれ、2 番目の非線形静的ブロックがない場合は、Hammerstein モデルと呼ばれます。
IDNLHW モデルは通常、以下の構文を使用して推定します。
M = NLHW(Data, Orders, InputNonlinearity, OutputNonlinearity).
ここで、Orders = [nb nf nk] は、線形伝達関数の次数と遅延を指定します。InputNonlinearity および OutputNonlinearity は、2 つの非線形ブロックの非線形関数を指定します。線形出力誤差 (OE) モデルは、自明な (単位ゲイン マッピング) 非線形性の場合に対応します。
Hammerstein モデルの推定 (出力非線形なし)
ここで、Orders = [nb bf nk] = [ones(2,6), ones(2,6), ones(2,6)] を選択します。これは、線形ブロックで、各出力が、6 つの出力に基づいた最初の 6 つの次数伝達関数の合計となることを意味します。入力非線形性が区分的線形関数で記述される Hammerstein モデル (出力非線形なし) を使用してみましょう。入力した 1 つの idPiecewiseLinear オブジェクトが、すべての 6 入力チャネルに自動的に展開されます。idUnitGain は非線形が存在しないことを示しています。
opt = nlhwOptions(); opt.SearchOptions.MaxIterations = 15; NN = [ones(2,6), ones(2,6), ones(2,6)]; InputNL = idPiecewiseLinear; % input nonlinearity OutputNL = idUnitGain; % output nonlinearity mhw1 = nlhw(z, NN, InputNL, OutputNL, opt)
mhw1 = <strong>Hammerstein-Wiener model with 2 outputs and 6 inputs</strong> Linear transfer function matrix corresponding to the orders: nb = [1 1 1 1 1 1; 1 1 1 1 1 1] nf = [1 1 1 1 1 1; 1 1 1 1 1 1] nk = [1 1 1 1 1 1; 1 1 1 1 1 1] Input nonlinearities: Input 1: Piecewise linear with 10 break-points Input 2: Piecewise linear with 10 break-points Input 3: Piecewise linear with 10 break-points Input 4: Piecewise linear with 10 break-points Input 5: Piecewise linear with 10 break-points Input 6: Piecewise linear with 10 break-points Output nonlinearities: Output 1: None Output 2: None Sample time: 0.02 seconds Status: Estimated using NLHW on time domain data "Motorized Camera". Fit to estimation data: [98.46;97.93]% FPE: 7.931, MSE: 2.217
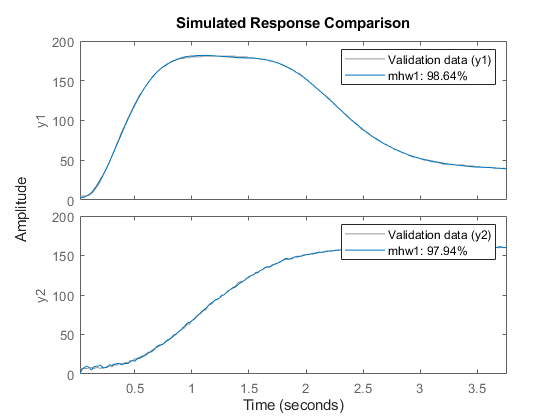
結果を compare で確認します。
compare(z, mhw1);
モデルのプロパティは、plot コマンドで可視化できます。
ブロック線図をクリックして、入力非線形 (UNL)、線形ブロックまたは出力非線形 (YNL) のビューを選択します。
線形ブロック ビューを選択した場合、既定の設定で、12 のチャネルすべてが縮小サイズで表示されます。チャネルの 1 つを選択して、わかりやすく表示します。ステップ応答、ボード線図、インパルス応答および極-零点図内で、プロットのタイプを選択できます。
plot(mhw1)
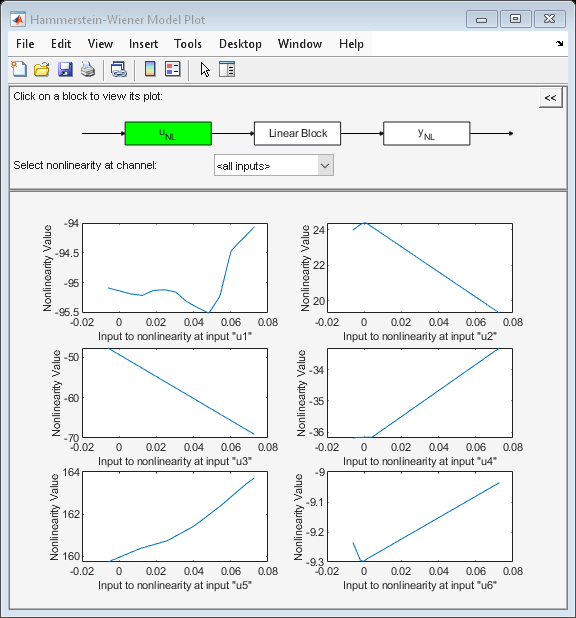
compare で示された結果は、非常に良好であり、以降のテストにも同じモデル次数を使用します。
nbnfnk = [ones(2,6), ones(2,6), ones(2,6)];
Wiener モデルの推定 (入力非線形なし)
Wiener モデルを使用してみましょう。入力非線形が存在しないことは、idUnitGain オブジェクト以外に、"[]" でも指定できます。
opt.SearchOptions.MaxIterations = 10; mhw2 = nlhw(z, nbnfnk, [], idPiecewiseLinear, opt)
mhw2 = <strong>Hammerstein-Wiener model with 2 outputs and 6 inputs</strong> Linear transfer function matrix corresponding to the orders: nb = [1 1 1 1 1 1; 1 1 1 1 1 1] nf = [1 1 1 1 1 1; 1 1 1 1 1 1] nk = [1 1 1 1 1 1; 1 1 1 1 1 1] Input nonlinearities: Input 1: None Input 2: None Input 3: None Input 4: None Input 5: None Input 6: None Output nonlinearities: Output 1: Piecewise linear with 10 break-points Output 2: Piecewise linear with 10 break-points Sample time: 0.02 seconds Status: Estimated using NLHW on time domain data "Motorized Camera". Fit to estimation data: [73.85;71.36]% FPE: 1.314e+05, MSE: 503.8
Hammerstein-Wiener モデルの推定 (入力および出力非線形)
Hammerstein-Wiener モデルの入力および出力非線形を指定します。
mhw3 = nlhw(z, nbnfnk,idSaturation, idPiecewiseLinear, opt)
mhw3 = <strong>Hammerstein-Wiener model with 2 outputs and 6 inputs</strong> Linear transfer function matrix corresponding to the orders: nb = [1 1 1 1 1 1; 1 1 1 1 1 1] nf = [1 1 1 1 1 1; 1 1 1 1 1 1] nk = [1 1 1 1 1 1; 1 1 1 1 1 1] Input nonlinearities: Input 1: Saturation with linear interval: [0.0103 0.0562] Input 2: Saturation with linear interval: [-0.00143 0.000909] Input 3: Saturation with linear interval: [-0.0947 -0.0185] Input 4: Saturation with linear interval: [-0.00385 0.00527] Input 5: Saturation with linear interval: [0.0195 0.13] Input 6: Saturation with linear interval: [-0.00302 0.000387] Output nonlinearities: Output 1: Piecewise linear with 10 break-points Output 2: Piecewise linear with 10 break-points Sample time: 0.02 seconds Status: Estimated using NLHW on time domain data "Motorized Camera". Fit to estimation data: [86.88;84.55]% FPE: 1.111e+04, MSE: 137.3
関数 idSaturation の限界値には、次のようにアクセスできます。
mhw3.InputNonlinearity(1).LinearInterval % view Linear Interval of saturation function
ans =
0.0103 0.0562
同様に、関数 idPiecewiseLinear のブレーク ポイントには、次のようにアクセスできます。
mhw3.OutputNonlinearity(1).BreakPoints
ans =
Columns 1 through 7
17.1233 34.2491 51.3726 68.4968 85.6230 102.7478 119.8742
2.6184 16.0645 45.5178 41.9621 62.3246 84.9038 112.2970
Columns 8 through 10
136.9991 154.1238 171.2472
135.4543 156.1016 173.2701
Hammerstein-Wiener モデル - 各種の非線形関数を使用
複数の非線形関数を、同じモデルに混在できます。- いずれかの出力チャネルで非線形 ("Hammerstein モデル") - 3 ユニットの入力チャネル #1 で区分的線形非線形 - 入力チャネル #2 で飽和非線形 - 入力チャネルl #3 でDead Zone 非線形 - 出力チャネルl #4 でシグモイド ネットワーク非線形 - 出力チャネル #5 で非線形 (unitgain オブジェクトで指定) - 5 ユニットの入力チャネル #6 でシグモイド ネットワーク非線形
選択したタイプの非線形マッピング関数オブジェクトからなる配列を作成して、それを入力非線形として推定関数 NLHW に渡せます。
inputNL = [idPiecewiseLinear; ... idSaturation; ... idDeadZone; ... idSigmoidNetwork; ... idUnitGain; ... idSigmoidNetwork(5)]; inputNL(1).NumberOfUnits = 3; opt.SearchOptions.MaxIterations = 25; mhw4 = nlhw(z, nbnfnk, inputNL, [], opt); % "[]" as the 4th input argument denotes no output nonlinearity
Hammerstein-Wiener モデル - SATURATION および DEADZONE に初期推定を指定
飽和の線形区間および不感帯の零点区間に対する初期推定は、これらのオブジェクトを作成したときに直接指定できます。また、これらの値を指定値に固定するかどうか (Free 属性を false に設定) や、推定が最小/最大境界に従うかどうか (Minimum 属性および Maximum 属性を使用) などの制約も指定できます。
初期推定で、飽和の線形区間を [10 200] に、不感帯の零点区間を [11 12] に設定するとします。さらに、飽和の上限を固定したままにします。この構成は次のようにして達成できます。
% Create nonlinear functions with initial guesses for properties. OutputNL1 = idSaturation([10 200]); OutputNL1.Free(2) = false; % the upper limit is a fixed value OutputNL2 = idDeadZone([11 12]); mhw5 = idnlhw(nbnfnk, [], [OutputNL1; OutputNL2], 'Ts',z.Ts);
推定器 nlhw ではなく、IDNLHW モデル オブジェクトのコンストラクター idnlhw を使用していることに注意してください。結果のモデル オブジェクト mhw5 は、データからまだ推定されていません。飽和関数および不感帯関数の限界値にアクセスできます。データからまだ推定を行っていないので、ここでは開始値のままになっています。
mhw5.OutputNonlinearity(1).LinearInterval % view the linear interval on saturation at first output channel after estimation mhw5.OutputNonlinearity(2).ZeroInterval % view the zero interval on dead zone at second output channel after estimation
ans =
10 200
ans =
11 12
推定後のこれらの限界値はどうなるでしょうか。
opt.SearchOptions.MaxIterations = 15; mhw5 = nlhw(z, mhw5, opt) % estimate the model from data mhw5.OutputNonlinearity(1).LinearInterval % show linear interval on saturation at first output channel after estimation mhw5.OutputNonlinearity(2).ZeroInterval % show zero interval on dead zone at second output channel after estimation
mhw5 =
<strong>Hammerstein-Wiener model with 2 outputs and 6 inputs</strong>
Linear transfer function matrix corresponding to the orders:
nb = [1 1 1 1 1 1; 1 1 1 1 1 1]
nf = [1 1 1 1 1 1; 1 1 1 1 1 1]
nk = [1 1 1 1 1 1; 1 1 1 1 1 1]
Input nonlinearities:
Input 1: None
Input 2: None
Input 3: None
Input 4: None
Input 5: None
Input 6: None
Output nonlinearities:
Output 1: Saturation with linear interval: [10 200]
Output 2: Dead Zone with zero interval: [11 12]
Sample time: 0.02 seconds
Status:
Estimated using NLHW on time domain data "Motorized Camera".
Fit to estimation data: [27.12;6.857]%
FPE: 3.373e+06, MSE: 4666
ans =
9.9974 200.0000
ans =
11.0020 12.0011
推定後の解析 - 異なるモデルの比較
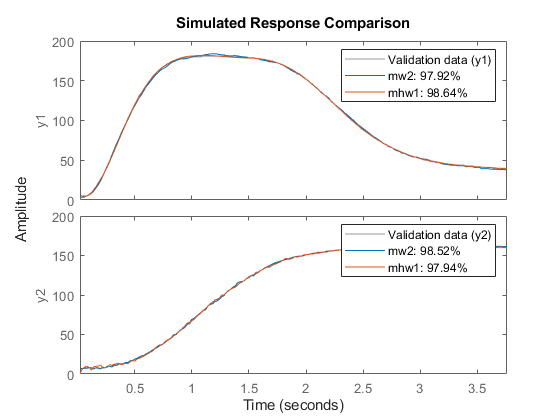
異なる特性のモデル (IDNLARX および IDNLHW) を、同じ compare コマンドで比較できます。
compare(z,mw2,mhw1)
warning(ws) % reset the warning state