モデル構造の選択: モデル次数と入力遅延の決定

スクリプトを開く

この例では、モデル構造の選択と構成を行う方法をいくつか示します。測定データを使用してモデルを推定するには、モデル構造 (状態空間または伝達関数など) とその次数 (たとえば、極および零点数) を事前に選択する必要があります。この選択は、モデル化を行っているシステムに関する予備知識に左右されますが、データそのものの解析にも影響されます。この例では、モデル次数と入力遅延を求めるためのオプションをいくつか説明します。

はじめに

モデル構造の選択は通常、推定の最初のステップとなります。構造には、状態空間、伝達関数および多項式形式 (ARX、ARMAX、OE、BJ など) のようにさまざまな可能性があります。ノイズ特性やフィードバックの表示など、システムに関する詳しい予備知識がない場合、適切な構造が選択できるかどうか、よくわからないかもしれません。また、構造を選択できても、対応するパラメーターを推定する前に、モデルの次数を指定する必要があります。System Identification Toolbox™ には、モデル次数を選択するためのツールがいくつか用意されています。

さらに、モデル次数の選択は、遅延の程度にも左右されます。入力遅延について正しく把握していると、他のモデル係数の次数を求める作業が容易になります。入力遅延の決定、モデル構造、および次数選択に関するいくつかのオプションを、以下に示します。

解析用のサンプルデータの選択と準備

この例は、iddemo1 でも使用したヘアドライヤーのデータを使用しています (「実際のラボ処理データからシンプルモデルの推定」)。この処理では、チューブから空気を送風します。空気はチューブの入口で加熱され、入力はヒーターに印加される電圧となります。出力は、チューブの出口での温度です。

まず、測定データを読み込み、基本的な前処理を行います。

load dry2

最初の半分の推定を行うためのデータセットと、2 番目の半分の検証を行うための基準セットを構成します。

ze = dry2(1:500);
zr = dry2(501:1000);

各セットのトレンド除去:

ze = detrend(ze);
zr = detrend(zr);

推定データの一部を見てみましょう。

plot(ze(200:350))

入力遅延の推定

入力から出力への時間遅延を求めるには、さまざまなオプションがあります。これらのオプションとは、以下のとおりです。

DELAYEST ユーティリティを使用する。
IMPULSEEST を使用して、インパルス応答のノンパラメトリック推定を行う。
異なる次数で状態空間モデル推定器 N4SID を使用し、'最適' なものの遅延を見つける。

delayest の使用:

上記のオプションを詳しく説明します。関数 delayest は、選択した次数の分子および分母多項式について、遅延の推定値を返します。この関数は、以下の ARX 構造を評価します。

y(t) + a1*y(t-1) + ... + ana*y(t-na) = b1*u(t-nk) + ...+bnb*u(t-nb-nk+1)

ここには各種の遅延が含まれ、最適適合を返すと思われる遅延値を選択します。この処理では、選択した値 na および nb が使用されます。

delay = delayest(ze) % na = nb = 2 is used, by default

delay =

     3

既定の設定では、値 3 が返されます。ただし、分子および分母多項式 (ここでは 2) の予想次数が変更された場合、この値も若干変わることがあります。以下に例を示します。

delay = delayest(ze,5,4)

delay =

     2

値 2 が返されます。delayest の動作の詳細を理解するため、複数の遅延を選択したときの損失関数を明示的に評価してみます。delayest の既定の設定である 2 次モデル (na=nb=2) を選択し、1 から 10 のすべての時間遅延を試します。異なるモデルの損失関数は、検証データセットを使用して算出されます。

V = arxstruc(ze,zr,struc(2,2,1:10));

検証データに最適な遅延を選択します。

[nn,Vm] = selstruc(V,0); % nn is given as [na nb nk]

選択した構造は、以下のとおりです。

nn

nn =

     2     2     3

ここで、最適モデルの遅延は nn(3) = 3 となります。

また、適合が遅延に依存するかどうかも確認できます。この情報は、2 番目の出力 Vm で返されます。2 次損失関数の対数が最初の行に示され、インデックス na、nb および nk は対応する損失関数の下の列に示されます。

Vm

Vm =

  Columns 1 through 7

   -0.1480   -1.3275   -1.8747   -0.2403   -0.0056    0.0736    0.1763
    2.0000    2.0000    2.0000    2.0000    2.0000    2.0000    2.0000
    2.0000    2.0000    2.0000    2.0000    2.0000    2.0000    2.0000
    1.0000    2.0000    3.0000    4.0000    5.0000    6.0000    7.0000

  Columns 8 through 10

    0.1906    0.1573    0.1474
    2.0000    2.0000    2.0000
    2.0000    2.0000    2.0000
    8.0000    9.0000   10.0000

The choice of 3 delays is thus rather clear, since the corresponding
loss is minimum.

impulse の使用

ダイナミクスの理解を深めるため、システムのインパルス応答を算出します。ノンパラメトリックインパルス応答モデルを算出するには、関数 impulseest を使用します。この応答を、標準偏差 3 で示される信頼区間でプロットします。

FIRModel = impulseest(ze);
clf
h = impulseplot(FIRModel);
showConfidence(h,3)

薄青の領域は、この推定で有意でない応答の信頼区間を示します。インパルス応答が、3 サンプルの後、"テイクオフ" する (不確実領域を出る) ことがわかります。これは、3 区間の遅延に相当します。

n4sid に基づいた状態空間評価の使用

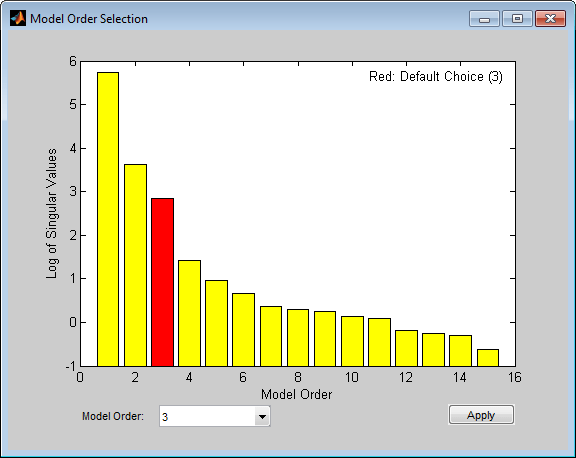
また、一連のパラメトリックモデルを使用して、"最適" モデルに対応する遅延を見つけることもできます。状態空間モデルの場合、次数範囲を同時に評価することができ、ハンケル特異値のプロットから最適な次数を選択できます。以下のコマンドを実行して、対話モードで n4sid を呼び出します。

m = n4sid(ze,1:15); % All orders between 1 and 15.

このプロットは、次数 3 が最適値であることを示します。これを選択した場合、モデル m のインパルス応答を算出します。

m = n4sid(ze, 3);
showConfidence(impulseplot(m),3)

ノンパラメトリックインパルス応答と同じように、入力から出力への遅延が 3 サンプルであることがわかります。

適切なモデル構造の選択

予備知識がまったくない場合、利用できるさまざまな選択肢を試して、最もふさわしいと思われるものを使用することをお勧めします。状態空間モデルは、モデルを推定するために指定する必要があるのが状態数だけであるため、適切な開始点となります。また、次の節で説明するように、最適次数を求める場合、n4sid を使用すると次数範囲を素早く評価できます。多項式モデルの場合、arx 推定器を使用すると、同様のメリットが得られます。さらに、出力誤差 (OE) モデルも、簡単であることから、多項式モデルの開始点として適切です。

モデル次数の決定

使用するモデル構造を決定したら、次の作業では、次数を決定します。一般に、その目的は、必要以上に高いモデル次数を使用しないようにすることです。この次数は、適合率の改善をモデル次数の関数として解析して求めます。この手順を実行する場合、検証には個別の独立したデータセットを使用することをお勧めします。個別の検証データセットを選択すると (たとえば zr)、過学習の検知を改善できます。

複数モデル次数の順次解析に加えて、一部のモデル構造では、最適次数の明示的な決定を行うことができます。ARX モデルの最適次数を選択する場合、関数 arxstruc および selstruc を使用できます。この例では、いずれも遅延値 3 により、最大 10 b パラメーターおよび 10 a パラメーターまで、100 の組み合わせすべてで適合を評価しています。

V = arxstruc(ze,zr,struc(1:10,1:10,3));

検証データセットの最適適合は、以下のように得られます。

nn = selstruc(V,0)

nn =

    10     4     3

高次数モデルで、適合がどれぐらい改善されたか確認してみましょう。この確認では、1 つの入力のみで関数 selstruc を使用します。この場合、使用したパラメーター数の関数として適合を示すプロットが作成されます。また、ユーザーには、パラメーター数を入力するようにプロンプトメッセージが表示されます。ルーチンで、最適適合を示すパラメーターが多い構造が選択されます。複数の異なるモデル構造で、同じパラメーター数が使用されることにご注意ください。次のコマンドを実行して、インタラクティブにモデル次数を選択します。

nns = selstruc(V) %invoke selstruc in an interactive mode

ここで、最適適合は nn = [4 4 3] となり、nn = [2 2 3] と比べてわずかに適合が改善されていることがわかります。

さらに、この問題には、高次数モデルを減らすという方向からアプローチすることもできます。次数が必要以上に高いと、測定ノイズを "モデル化" するときに余分なパラメーターが基本的に使用されることになります。このような "余分" 極では、推定の精度が低下します (大きな信頼区間)。近くにある零点で極がキャンセルされた場合、システムの必須ダイナミクスを捕捉するのに、この極-零点のペアが不要である可能性が考えられます。

ここでの例では、4 次モデルを算出しています。

th4 = arx(ze,[4 4 3]);

このモデルの極-零点構成を確認してみましょう。また、標準偏差 3 に対応する極/零点の信頼領域を含め、その推定精度と、極と零点それぞれの近接度を確認することもできます。

h = iopzplot(th4);
showConfidence(h,3)

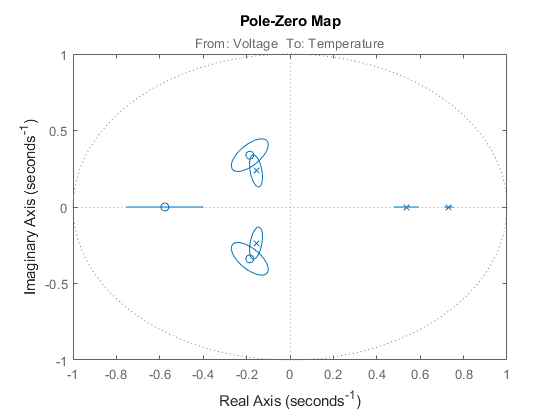
2 つの複素共役極および零点重複の信頼区間は、お互いがキャンセルしあう可能性が高いことを示しています。このため、2 次モデルで十分であると考えられます。この実証に基づき、2 次 ARX モデルを算出します。

th2 = arx(ze,[2 2 3]);

このモデル (th2) が検証データセットをどの程度再現できるかをテストできます。2 つのモデルの出力と実際の出力 (中間の 200 データ点をプロット) を比較し、シミュレートするには compare ユーティリティを使用します。

compare(zr(150:350),th2,th4)

このプロットは、次数を 4 から 2 に減らしても、有意な精度の損失がないことを示します。また、このモデルの残差 (「レフトオーバー」)、すなわち、モデルで説明されないままの部分を確認することもできます。

e = resid(ze,th2);
plot(e(:,1,[])), title('The residuals')

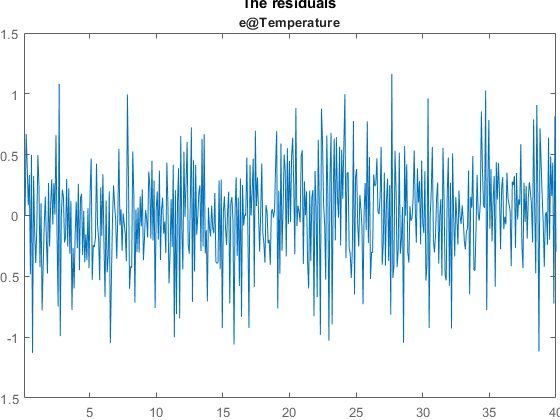
出力の信号レベルと比較して、残差が非常に少なく、入力と残差の間に (完璧にないわけではないが) 有意な相関関係がないことがわかります。したがって、モデル th2 に (とりあえず) 満足できます。

状態空間構造のモデル次数を求めてみましょう。前述のように、遅延は 3 サンプルとなります。n4sid で 3 サンプルの合計ラグを使用して、1 から 15 までのすべての次数を試すことができます。以下のコマンドを実行して、インタラクティブに各種の次数を試し、いずれかを選択します。

ms = n4sid(ze,[1:15],'InputDelay',2); %n4sid estimation with variable orders

"InputDelay" を 2 に設定した理由は、n4sid は既定で、直達のないモデル (入力と出力の間に 1 サンプルのラグをもつ) を推定するためです。上の図に示した既定の次数は 3 であり、前述の結果ともよく一致しています。最後に、検証データの測定出力の再現において、状態空間モデル ms と ARX モデル th2 を比較します。

ms = n4sid(ze,3,'InputDelay',2);
compare(zr,ms,th2)

この比較プロットは、2 つのモデルが実質的に同じであることを示します。

まとめ

この例では、適切なモデル次数を選択するためのオプションをいくつか紹介しました。遅延を事前に求めておくと、次数の選択が容易になります。ARX および状態空間構造では、モデル次数のセット全体を自動的に評価し、そこから最適な次数を選択する専用ツール (arx および n4sid 推定器) を使用できます。この実例で判明した情報 (arxstruc、selstruc、n4sid および delayest などのユーティリティを使用) は、BJ や ARMAX といった他の構造のモデルを推定する開始点として使用できます。