System Identification Toolbox を使用した構造化されたユーザー定義モデルの構築
この例では、ユーザー定義モデル構造でパラメーターを推定する方法を説明します。このような構造は IDGREY (線形状態空間) または IDNLGREY (非線形状態空間) モデルで指定されます。構造を割り当て、パラメーターを指定し、依存性を作成する方法を検討します。
実験データ
(シミュレート) DC モーターから生じたデータを検討します。まず、データを読み込みます。
load dcmdata y u
行列 y には、2 つの出力が含まれます。y1 はモーター シャフトの角度位置で、y2 は角速度です。400 件のデータ サンプルがあり、サンプル時間は 0.1 秒です。入力は、ベクトル u に含まれます。これは、モーターへの入力電圧です。
z = iddata(y,u,0.1); % The IDDATA object z.InputName = 'Voltage'; z.OutputName = {'Angle';'AngVel'}; plot(z(:,1,:))

図: 測定データ: 電圧と角度
plot(z(:,2,:))

図: 測定データ: 電圧と角速度
モデル構造の選択
d/dt x = A x + B u + K e
y = C x + D u + eDC モーターのモデルを構築します。モーターのダイナミクスはよく知られています。角度位置に x1 を、角速度に x2 を選択した場合、細部に煩わされることなく、以下の特性の状態空間モデルを簡単に設定できます(Ljung (1999) の例 4.1 を参照)。
| 0 1 | | 0 |
d/dt x = | | x + | | u
| 0 -th1 | | th2 | | 1 0 |
y = | | x
| 0 1 |パラメーター th1 はモーターの逆時定数、th2 は th2/th1 が入力から角速度への静的ゲインとなるような値です (モーターの物理パラメーターに th1 と th2 がどのように関連しているかについては、Ljung (1987) を参照してください)。観測されたデータから、これらの 2 つのパラメーターを推定します。前述のモデル構造 (パラメーター化状態空間) は、MATLAB® で IDSS および IDGREY モデルを使用して表示できます。これらのモデルにより、実験データを使用して、パラメーターを推定できます。
ノミナル (初期) モデルの指定
th1=1、th2=0.28 とすると、ノミナル モデルまたは初期モデルが得られます。
A = [0 1; 0 -1]; % initial guess for A(2,2) is -1 B = [0; 0.28]; % initial guess for B(2) is 0.28 C = eye(2); D = zeros(2,1);
IDSS モデル オブジェクトを作成します。
ms = idss(A,B,C,D);
このモデルは行列、行列の値 (推定できる自由要素)、行列の値の上限と下限により表されます。
ms.Structure.a
ans =
Name: 'A'
Value: [2×2 double]
Minimum: [2×2 double]
Maximum: [2×2 double]
Free: [2×2 logical]
Scale: [2×2 double]
Info: [2×2 struct]
1x1 param.Continuous
ms.Structure.a.Value ms.Structure.a.Free
ans =
0 1
0 -1
ans =
2×2 logical array
1 1
1 1
IDSS モデルを使用した空き (独立) パラメーターの指定
ここで注意が必要なのは、推定できる自由パラメーターは A(2,2) と B(2,1) のみであるという点です。
ms.Structure.a.Free = [0 0; 0 1]; ms.Structure.b.Free = [0; 1]; ms.Structure.c.Free = 0; % scalar expansion used ms.Structure.d.Free = 0; ms.Ts = 0; % This defines the model to be continuous
初期モデル
ms % Initial model
ms =
Continuous-time identified state-space model:
dx/dt = A x(t) + B u(t) + K e(t)
y(t) = C x(t) + D u(t) + e(t)
A =
x1 x2
x1 0 1
x2 0 -1
B =
u1
x1 0
x2 0.28
C =
x1 x2
y1 1 0
y2 0 1
D =
u1
y1 0
y2 0
K =
y1 y2
x1 0 0
x2 0 0
Parameterization:
STRUCTURED form (some fixed coefficients in A, B, C).
Feedthrough: none
Disturbance component: none
Number of free coefficients: 2
Use "idssdata", "getpvec", "getcov" for parameters and their uncertainties.
Status:
Created by direct construction or transformation. Not estimated.
IDSS モデルの自由パラメーターの推定
パラメーターの予測誤差 (最大数尤度) 推定が、以下のように算出されます。
dcmodel = ssest(z,ms,ssestOptions('Display','on')); dcmodel
dcmodel =
Continuous-time identified state-space model:
dx/dt = A x(t) + B u(t) + K e(t)
y(t) = C x(t) + D u(t) + e(t)
A =
x1 x2
x1 0 1
x2 0 -4.013
B =
Voltage
x1 0
x2 1.002
C =
x1 x2
Angle 1 0
AngVel 0 1
D =
Voltage
Angle 0
AngVel 0
K =
Angle AngVel
x1 0 0
x2 0 0
Parameterization:
STRUCTURED form (some fixed coefficients in A, B, C).
Feedthrough: none
Disturbance component: none
Number of free coefficients: 2
Use "idssdata", "getpvec", "getcov" for parameters and their uncertainties.
Status:
Estimated using SSEST on time domain data "z".
Fit to estimation data: [98.35;84.42]%
FPE: 0.001071, MSE: 0.1192
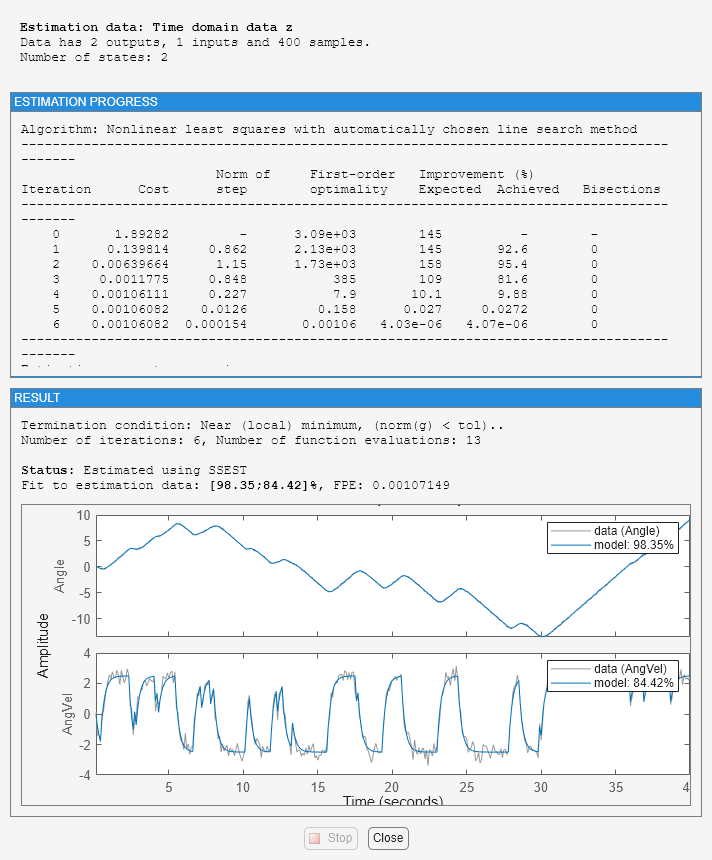
パラメーターの推定値は、データをシミュレートしたときに使用した数値と非常に近接しています (-4 と 1)。モデルの質を評価するには、実際の入力を使用してモデルをシミュレートし、実際の出力と比較します。
compare(z,dcmodel);

たとえば、零点と極およびその不確実領域をプロットします。モデルの精度が高いため、標準偏差 3 に対応する領域を表示します。原点での極は、モデル構造の一部であり、角速度から位置への積分器であるため、絶対に確実であることがわかります。
clf showConfidence(iopzplot(dcmodel),3)

いくつか変更を行ってみましょう。A 行列の 1,2 要素 (1 に固定) から、x2 が x1 の微分となります。センサーが調整されていない場合、不明の比例定数が存在することが考えられます。このような定数の推定を含めるため、A(1,2) を "解放" し、再び推定を行います。
dcmodel2 = dcmodel; dcmodel2.Structure.a.Free(1,2) = 1; dcmodel2 = pem(z,dcmodel2);

得られるモデルは以下のようになります。
dcmodel2
dcmodel2 =
Continuous-time identified state-space model:
dx/dt = A x(t) + B u(t) + K e(t)
y(t) = C x(t) + D u(t) + e(t)
A =
x1 x2
x1 0 0.9975
x2 0 -4.011
B =
Voltage
x1 0
x2 1.004
C =
x1 x2
Angle 1 0
AngVel 0 1
D =
Voltage
Angle 0
AngVel 0
K =
Angle AngVel
x1 0 0
x2 0 0
Parameterization:
STRUCTURED form (some fixed coefficients in A, B, C).
Feedthrough: none
Disturbance component: none
Number of free coefficients: 3
Use "idssdata", "getpvec", "getcov" for parameters and their uncertainties.
Status:
Estimated using PEM on time domain data "z".
Fit to estimation data: [98.35;84.42]%
FPE: 0.001077, MSE: 0.1192
推定した A(1,2) が 1 に近いことがわかります。2 つのモデルを比較するには、compare コマンドを使用します。
compare(z,dcmodel,dcmodel2)

IDGREY オブジェクトを使用した連動パラメーターによるモデルの指定
DC モーターの静的ゲインを正確に把握しているとします (入力電圧から角速度へ、たとえば、前に行ったステップ応答実験)。静的ゲインが G、モーターの時定数が t である場合、状態空間モデルは以下のようになります。
|0 1| | 0 |
d/dt x = | |x + | | u
|0 -1/t| | G/t | |1 0|
y = | | x
|0 1|G が既知であるため、異なる行列の要素間に依存性があります。これを記述するには、以前使用した自由パラメーターを使用する方法では不十分です。このため、所定のパラメーター ベクトルそれぞれを入力とし、A、B、C、D の各行列、および任意で K および X0 行列を出力として生成する MATLAB ファイルを作成する必要があります。また、ユーザーが、このファイルを編集しなくても、モデル構造の一部を変更できるように、補助引数を入力として使用します。この場合、既知の静的ゲイン G を引数として入力します。作成されたファイルの名前は 'motorDynamics.m' です。
type motorDynamics
function [A,B,C,D,K,X0] = motorDynamics(par,ts,aux) %MOTORDYNAMICS ODE file representing the dynamics of a motor. % % [A,B,C,D,K,X0] = motorDynamics(Tau,Ts,G) % returns the State Space matrices of the DC-motor with % time-constant Tau (Tau = par) and known static gain G. The sample % time is Ts. % % This file returns continuous-time representation if input argument Ts % is zero. If Ts>0, a discrete-time representation is returned. To make % the IDGREY model that uses this file aware of this flexibility, set the % value of Structure.FcnType property to 'cd'. This flexibility is useful % for conversion between continuous and discrete domains required for % estimation and simulation. % % See also IDGREY, IDDEMO7. % L. Ljung % Copyright 1986-2015 The MathWorks, Inc. t = par(1); G = aux(1); A = [0 1;0 -1/t]; B = [0;G/t]; C = eye(2); D = [0;0]; K = zeros(2); X0 = [0;0]; if ts>0 % Sample the model with sample time Ts s = expm([[A B]*ts; zeros(1,3)]); A = s(1:2,1:2); B = s(1:2,3); end
このモデル構造に対応する IDGREY モデル オブジェクトを作成します。想定される時定数は以下のとおりです。
par_guess = 1;
また、補助変数 G (ゲイン) の値 0.25 とサンプル時間も与えます。
aux = 0.25; dcmm = idgrey('motorDynamics',par_guess,'cd',aux,0);
時定数は、以下のように推定されます。
dcmm = greyest(z,dcmm,greyestOptions('Display','on'));

これで、モーターの時定数が直接推定されました。値は前の推定と非常によく一致しています。
dcmm
dcmm =
Continuous-time linear grey box model defined by "motorDynamics" function:
dx/dt = A x(t) + B u(t) + K e(t)
y(t) = C x(t) + D u(t) + e(t)
A =
x1 x2
x1 0 1
x2 0 -4.006
B =
Voltage
x1 0
x2 1.001
C =
x1 x2
Angle 1 0
AngVel 0 1
D =
Voltage
Angle 0
AngVel 0
K =
Angle AngVel
x1 0 0
x2 0 0
Model parameters:
Par1 = 0.2496
Parameterization:
ODE Function: motorDynamics
(parametrizes both continuous- and discrete-time equations)
Disturbance component: parameterized by the ODE function
Initial state: parameterized by the ODE function
Number of free coefficients: 1
Use "getpvec", "getcov" for parameters and their uncertainties.
Status:
Estimated using GREYEST on time domain data "z".
Fit to estimation data: [98.35;84.42]%
FPE: 0.00107, MSE: 0.1193
このモデルを使用して、各種のテストに進むことができます。すべてのコマンドの構文は、前のケースと同じです。たとえば、idgrey モデルを他の状態空間モデルと比較できます。
compare(z,dcmm,dcmodel)

明らかに非常に近いものとなっています。
多変量 ARX モデルの推定
ツールボックスの状態空間部分では、多変量 (複数出力) ARX モデルも処理します。多変量 ARX モデルとは、以下を意味します。
A(q) y(t) = B(q) u(t) + e(t)
ここで、A(q) は ny | ny 行列で、その要素は、遅れ演算子 1/q の多項式となります。k-l 要素は、以下のように指定します。
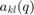
ここで、以下となります。

したがって、次数 nakl の 1/q における多項式となります。
同様に、B(q) は ny | nu 行列で、その kj 要素は以下のとおりです。

入力番号 j から出力番号 k への遅延は nkkj です。これらを作成する最も一般的な方法は、ARX コマンドを使用することです。次数は、nn = [na nb nk] のように指定します。ここで na は ny-by-ny 行列、その kj 番目の要素は nakj です。nb と nk も同じように定義されます。
dc データでいくつかの ARX モデルをテストしてみましょう。まず、一般的な 2 次モデルを構築します。
dcarx1 = arx(z,'na',[2,2;2,2],'nb',[2;2],'nk',[1;1])
dcarx1 =
Discrete-time ARX model:
Model for output "Angle": A(z)y_1(t) = - A_i(z)y_i(t) + B(z)u(t) + e_1(t)
A(z) = 1 - 0.5545 z^-1 - 0.4454 z^-2
A_2(z) = -0.03548 z^-1 - 0.06405 z^-2
B(z) = 0.004243 z^-1 + 0.006589 z^-2
Model for output "AngVel": A(z)y_2(t) = - A_i(z)y_i(t) + B(z)u(t) + e_2(t)
A(z) = 1 - 0.2005 z^-1 - 0.2924 z^-2
A_1(z) = 0.01849 z^-1 - 0.01937 z^-2
B(z) = 0.08642 z^-1 + 0.03877 z^-2
Sample time: 0.1 seconds
Parameterization:
Polynomial orders: na=[2 2;2 2] nb=[2;2] nk=[1;1]
Number of free coefficients: 12
Use "polydata", "getpvec", "getcov" for parameters and their uncertainties.
Status:
Estimated using ARX on time domain data "z".
Fit to estimation data: [97.87;83.44]% (prediction focus)
FPE: 0.002157, MSE: 0.1398
結果 dcarx1 は、IDPOLY モデルとして格納され、以前のすべてのコマンドが適用されます。たとえば、以下のように、ARX 多項式を明示的に求めることができます。
dcarx1.a
ans =
2×2 cell array
{[1 -0.5545 -0.4454]} {[0 -0.0355 -0.0640]}
{[ 0 0.0185 -0.0194]} {[1 -0.2005 -0.2924]}
結果は cell 配列となり、たとえば dcarx1.a の {1,2} 要素は前述の多項式 A(1,2) で、y2 が y1 に関連付けられています。
また、構造をテストすることもできます。この場合、1 次フィルターで y2 を処理し、y1 が得られることがわかります (角度は、角速度の積分です)。さらに、入力から出力番号 2 への 1 次ダイナミクスを想定できます。
na = [1 1; 0 1]; nb = [0 ; 1]; nk = [1 ; 1]; dcarx2 = arx(z,[na nb nk])
dcarx2 =
Discrete-time ARX model:
Model for output "Angle": A(z)y_1(t) = - A_i(z)y_i(t) + B(z)u(t) + e_1(t)
A(z) = 1 - 0.9992 z^-1
A_2(z) = -0.09595 z^-1
B(z) = 0
Model for output "AngVel": A(z)y_2(t) = B(z)u(t) + e_2(t)
A(z) = 1 - 0.6254 z^-1
B(z) = 0.08973 z^-1
Sample time: 0.1 seconds
Parameterization:
Polynomial orders: na=[1 1;0 1] nb=[0;1] nk=[1;1]
Number of free coefficients: 4
Use "polydata", "getpvec", "getcov" for parameters and their uncertainties.
Status:
Estimated using ARX on time domain data "z".
Fit to estimation data: [97.52;81.46]% (prediction focus)
FPE: 0.003452, MSE: 0.177
構築した異なるモデルを比較するには、以下を使用します。
compare(z,dcmodel,dcmm,dcarx2)

最後に、異なるモデルの入力から出力で取得したボード線図を比較するには、bode を使用できます。最初の出力:
dcmm2 = idss(dcmm); % convert to IDSS for subreferencing bode(dcmodel(1,1),'r',dcmm2(1,1),'b',dcarx2(1,1),'g')
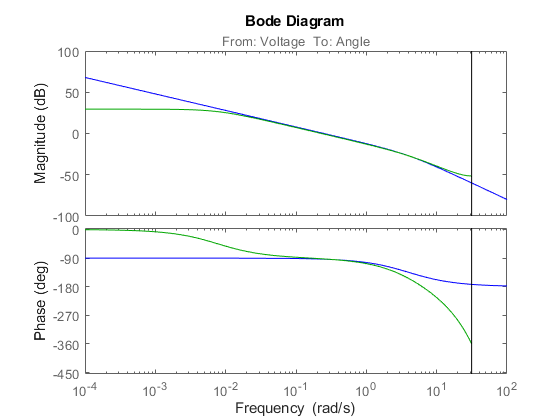
Second output:
bode(dcmodel(2,1),'r',dcmm2(2,1),'b',dcarx2(2,1),'g')

最初のモデル 2 つは、ほぼ一致しています。ARX モデルは、方程式誤差による非ホワイト ノイズのためバイアスが生じており、あまり良好ではありません(シミュレーションでは、測定ホワイト ノイズが見られました)。
まとめ
事前に選択した構造によるモデルの推定は、System Identification ツールボックスを使用して実行できます。状態空間形式では、パラメーターは既知の値に固定することができ、また所定の範囲内に収まるよう制限することもできます。パラメーターや他の制約条件の間に関係を指定する必要がある場合、IDGREY オブジェクトを使用できます。IDGREY モデルは、状態空間システム パラメーターを推定するときに、ユーザー指定の MATLAB ファイルを評価します。多変量 ARX モデルでは、ユーザー指定の構造で複数出力のモデルを短時間で推定するため、別のオプションが使用できます。