Jet Pump
(To be removed) Jet liquid-liquid pump
The Hydraulics (Isothermal) library will be removed in a future release. Use the Isothermal Liquid library instead.
For more information on updating your models, see Upgrading Hydraulic Models to Use Isothermal Liquid Blocks.
Libraries:
Simscape /
Fluids /
Hydraulics (Isothermal) /
Pumps and Motors
Description
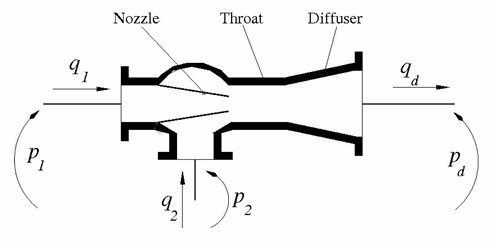
The Jet Pump block represents a jet liquid-liquid pump consisting of a nozzle, throat, and diffuser, as shown in this illustration.
The model is based on these equations, described in [1]:
| (1) |
| (2) |
| (3) |
where:
| q1 | Primary flow rate pumped through the nozzle |
| q2 | Secondary flow rate |
| qd | Output flow rate |
| p1 | Pressure at the nozzle inlet |
| p2 | Pressure at the secondary flow rate inlet |
| p0 | Pressure at the throat inlet |
| pd | Pressure at the pump outlet |
| An | Nozzle area |
| Ath | Throat area |
| a | Diffuser area ratio, Ath / Ad |
| Ad | Diffuser outlet area |
| Kn | Nozzle hydraulic loss coefficient |
| Ken | Throat entry hydraulic loss coefficient |
| Kth | Throat hydraulic loss coefficient |
| Kdi | Diffuser hydraulic loss coefficient |
| ρ | Fluid density |
Equation 1 describes the nozzle, Equation 2 describes the throat entry, and Equation 3 describes the combination of the throat and the diffuser. The equations correspond to a standard configuration of the pump, where all the longitudinal dimensions conform to established, empirically determined values. For more details, see [1].
The pump parameters are closely related to each other, and the methodology described in [1] is recommended to determine their initial values.
Variables
To set the priority and initial target values for the block variables prior to simulation, use the Initial Targets section in the block dialog box or Property Inspector. For more information, see Set Priority and Initial Target for Block Variables.
Nominal values provide a way to specify the expected magnitude of a variable in a model. Using system scaling based on nominal values increases the simulation robustness. Nominal values can come from different sources, one of which is the Nominal Values section in the block dialog box or Property Inspector. For more information, see Modify Nominal Values for a Block Variable.
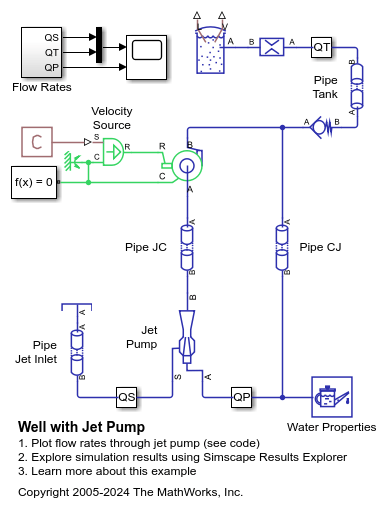
Examples
Assumptions and Limitations
The model is based on the one-dimensional theory.
The primary and secondary flows enter the mixing throat with uniform velocity distribution, and the mixed flow leaves the diffuser with uniform velocity distribution.
The fluid in the primary and secondary flows is the same.
The fluid is assumed to be incompressible and containing no gas.
Ports
Conserving
Parameters
References
[1] I.J. Karassic, J.P. Messina, P. Cooper, C.C. Heald, Pump Handbook, Fourth edition, McGraw-Hill, NY, 2008