Distributed Arithmetic for FIR Filters
Distributed Arithmetic Overview
Distributed Arithmetic (DA) is a widely used technique for implementing sum-of-products computations without the use of multipliers. Designers frequently use DA to build efficient Multiply-Accumulate Circuitry (MAC) for filters and other DSP applications.
The main advantage of DA is its high computational efficiency. DA distributes multiply and accumulate operations across shifters, lookup tables (LUTs), and adders in such a way that conventional multipliers are not required.
The coder supports DA in HDL code generated for several single-rate and multirate FIR filter structures for fixed-point filter designs. (See Requirements and Considerations for Generating Distributed Arithmetic Code. )
This section briefly summarizes of the operation of DA. Detailed discussions of the theoretical foundations of DA appear in these publications.
Meyer-Baese, U., Digital Signal Processing with Field Programmable Gate Arrays, Second Edition, Springer, pp 88–94, 128–143.
White, S.A., Applications of Distributed Arithmetic to Digital Signal Processing: A Tutorial Review. IEEE ASSP Magazine, Vol. 6, No. 3.
In a DA realization of a FIR filter structure, a sequence of input data words of width
W is fed through a parallel to serial shift register. This feedthrough
produces a serialized stream of bits. The serialized data is then fed to a bit-wide shift
register. This shift register serves as a delay line, storing the bit serial data
samples.
The delay line is tapped (based on the input word size W), to form a
W-bit address that indexes into a lookup table (LUT). The LUT stores
the possible sums of partial products over the filter coefficients space. A shift and adder
(scaling accumulator) follow the LUT. This logic sequentially adds the values obtained from
the LUT.
A table lookup is performed sequentially for each bit (in order of significance starting from the LSB). On each clock cycle, the LUT result is added to the accumulated and shifted result from the previous cycle. For the last bit (MSB), the table lookup result is subtracted, accounting for the sign of the operand.
This basic form of DA is fully serial, operating on one bit at a time. If the input
data sequence is W bits wide, then a FIR structure takes
W clock cycles to compute the output. Symmetric and asymmetric FIR
structures are an exception, requiring W+1 cycles, because one additional
clock cycle is required to process the carry bit of the preadders.
Improving Performance with Parallelism
The inherently bit serial nature of DA can limit throughput. To improve throughput,
the basic DA algorithm can be modified to compute more than one bit-sum at a time. The
number of simultaneously computed bit sums is expressed as a power of two called the
DA radix. For example, a DA radix of 2 (2^1)
indicates that a one bit-sum is computed at a time. A DA radix of 4
(2^2) indicates that a two bit-sums are computed at a time, and so
on.
To compute more than one bit-sum at a time, the coder replicates the LUT. For example, to perform DA on two bits at a time (radix 4), the odd bits are fed to one LUT and the even bits are simultaneously fed to an identical LUT. The LUT results corresponding to odd bits are left-shifted before they are added to the LUT results corresponding to even bits. This result is then fed into a scaling accumulator that shifts its feedback value by two places.
Processing more than one bit at a time introduces a degree of parallelism into the
operation, which can improve performance at the expense of
area. The DARadix property lets you specify
the number of bits processed simultaneously in DA.
Reducing LUT Size
The size of the LUT grows exponentially with the order of the filter. For a filter
with N coefficients, the LUT must have 2^N values.
For higher-order filters, LUT size must be reduced to reasonable levels. To reduce the
size, you can subdivide the LUT into several LUTs, called LUT
partitions. Each LUT partition operates on a different set of taps. The
results obtained from the partitions are summed.
For example, for a 160 tap filter, the LUT size is (2^160)*W bits,
where W is the word size of the LUT data. You can achieve a significant
reduction in LUT size by dividing the LUT into 16 LUT partitions, each taking 10 inputs
(taps). This division reduces the total LUT size to 16*(2^10)*W
bits.
Although LUT partitioning reduces LUT size, the architecture uses more adders to sum the LUT data.
The DALUTPartition property
lets you specify how the LUT is partitioned in DA.
Requirements and Considerations for Generating Distributed Arithmetic Code
The coder lets you control how DA code is generated using the
DALUTPartition and DARadix properties (or equivalent
Generate HDL tool options). Before using these properties, review these general
requirements, restrictions, and other considerations for generation of DA code.
Supported Filter Types
The coder supports DA in HDL code generated for these single-rate and multirate FIR filter structures:
direct form (
dfilt.dffirordsp.FIRFilter)direct form symmetric (
dfilt.dfsymfirordsp.FIRFilter)direct form asymmetric (
dfilt.dfasymfirordsp.FIRFilter)dsp.FIRDecimatordsp.FIRInterpolator
Fixed-Point Quantization Required
Generation of DA code is supported only for fixed-point filter designs.
Specifying Filter Precision
The data path in HDL code generated for the DA architecture is optimized for full precision computations. The filter casts the result to the output data size at the final stage. If your filter object is set to use full precision data types, numeric results from simulating the generated HDL code are bit-true to the output of the original filter object.
If your filter object has customized word or fraction lengths, the generated DA code may produce numeric results that are different than the output of the original filter object.
Coefficients with Zero Values
DA ignores taps that have zero-valued coefficients and reduces the size of the DA LUT accordingly.
Considerations for Symmetric and Asymmetric Filters
For symmetric and asymmetric FIR filters:
A bit-level preadder or presubtractor is required to add tap data values that have coefficients of equal value and/or opposite sign. One extra clock cycle is required to compute the result because of the additional carry bit.
The coder takes advantage of filter symmetry. This symmetry reduces the DA LUT size substantially, because the effective filter length for these filter types is halved.
Holding Input Data in a Valid State
Partitioned distributed arithmetic architectures implement internal clock rates higher
than the input rate. In such filter implementations, there are N cycles
(N >= 2) of the base clock for each input sample. You can specify
how many clock cycles the test bench holds the input data values in a valid state.
When you select Hold input data between samples (the default), the test bench holds the input data values in a valid state for
Nclock cycles.When you clear Hold input data between samples, the test bench holds input data values in a valid state for only one clock cycle. For the next
N-1cycles, the test bench drives the data to an unknown state (expressed as'X') until the next input sample is clocked in. Forcing the input data to an unknown state verifies that the generated filter code registers the input data only on the first cycle.
Distributed Arithmetic via generatehdl Properties
Two properties specify distributed arithmetic options to the
generatehdl function:
DALUTPartition— Number and size of lookup table (LUT) partitions.DARadix— Number of bits processed in parallel.
You can use the helper function hdlfilterdainfo to explore possible partitions and radix settings for your
filter.
For examples, see
Distributed Arithmetic Options in the Generate HDL Tool
The Generate HDL tool provides several options related to DA code generation.
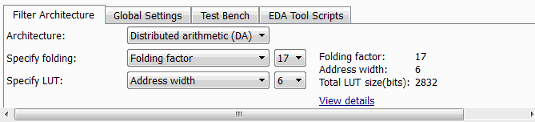
The Architecture pop-up menu, which lets you enable DA code generation and displays related options.
The Specify folding drop-down menu, which lets you directly specify the folding factor, or set a value for the
DARadixproperty.The Specify LUT drop-down menu, which lets you directly set a value for the
DALUTPartitionproperty. You can also select an address width for the LUT. If you specify an address width, the coder uses input LUTs as required.
The Generate HDL tool initially displays default DA-related option values that
correspond to the current filter design. For the requirements for setting these options, see
DALUTPartition and DARadix.
To specify DA code generation using the Generate HDL tool, follow these steps:
Design a FIR filter (using Filter Designer, Filter Builder, or MATLAB® commands) that meets the requirements described in Requirements and Considerations for Generating Distributed Arithmetic Code.
Open the Generate HDL tool.
Select
Distributed Arithmetic (DA)from the Architecture pop-up menu.When you select this option, the related Specify folding and Specify LUT options are displayed below the Architecture menu. This figure shows the default DA options for a direct form FIR filter.

Select one of these options from the Specify folding drop-down menu.
Folding factor(default): Select a folding factor from the drop-down menu to the right of Specify folding. The menu contains an exhaustive list of folding factor options for the filter.DA radix: Select the number of bits processed simultaneously, expressed as a power of 2. The defaultDA radixvalue is2, specifying processing of one bit at a time, or fully serial DA. If desired, set theDA radixfield to a nondefault value.
Select one of these options from the Specify LUT drop-down menu.
Address width(default): Select from the drop-down menu to the right of Specify LUT. The menu contains an exhaustive list of LUT address widths for the filter.Partition: Select, or enter, a vector specifying the number and size of LUT partitions.
Set other HDL options as required, and generate code. Invalid or illegal values for LUT Partition or DA Radix are reported at code generation time.
Viewing Detailed DA Options
As you interact with the Specify folding and Specify
LUT options you can see the results of your choice in three display-only
fields: Folding factor, Address width, and
Total LUT size (bits).
In addition, when you click the View details hyperlink, the coder displays a report showing complete DA architectural details for the current filter, including:
Filter lengths
Complete list of applicable folding factors and how they apply to the sets of LUTs
Tabulation of the configurations of LUTs with total LUT Size and LUT details
This figure shows a typical report.

DA Interactions with Other HDL Options
When Distributed Arithmetic (DA) is selected in the
Architecture menu, some other HDL options change automatically to
settings that correspond to DA code generation:
Coefficient multipliers is set to
Multiplierand disabled.FIR adder style is set to
Treeand disabled.Add input register (in the Ports pane) is selected and disabled. (An input register, used as part of a shift register, is used in DA code.)
Add output register (in the Ports pane) is selected and disabled.
