このページは機械翻訳を使用して翻訳されました。最新版の英語を参照するには、ここをクリックします。

溶接梁の設計最適化

この例では、梁の強度とコストのトレードオフを調べる方法を示します。Debら[1]やRayとLiew[2]など、いくつかの出版物では、この例をさまざまな多目的アルゴリズムのテスト問題として使用しています。

この例のビデオ概要については、多目的最適化のためのパレート集合を参照してください。

問題の説明

以下のスケッチはRayとLiew [2]から改変したものである。

このスケッチは、基板に溶接されたビームを表しています。ビームは基板から距離 L にある荷重 P を支えます。梁は、それぞれ長さ l、厚さ h の上部溶接と下部溶接によって基板に溶接されます。梁の断面は長方形で、幅は b、高さは t です。梁の材質は鋼鉄です。

2つの目標は、梁の製造コストと、荷重Pを受けた際の梁端部のたわみです。荷重Pは6,000ポンドに固定され、距離Lは14インチに固定されています。

設計変数は次のとおりです。

x(1) = h、溶接部の厚さ
x(2) = l、溶接部の長さ
x(3) = t、梁の高さ
x(4) = b、ビームの幅

梁の製造コストは、梁の材料の量 $(l + L) t b$ と溶接部の材料の量 $l h^{2}$ の合計に比例します。引用した論文の比例定数を用いて、最初の目的は

$F_{1} (x) = 1.10471 x_{1}^{2} x_{2} + 0.04811 x_{3} x_{4} (14 + x_{2}) .$

ビームの偏向は P に比例し、 $b t^{3}$ に反比例します。ここでも、引用した論文の比例定数を用いると、2番目の目的は

$F_{2} (x) = \frac{P}{x_{4} x_{3}^{3}} C$ 、ここで $C = \frac{4 (14)^{3}}{30 \times 1 0^{6}} \approx 3.6587 \times 1 0^{- 4}$ と $P = 6, 000$ 。

問題にはいくつかの制約があります。

溶接厚さは梁の幅を超えることはできません。記号では x(1) <= x(4) である。ツールボックス構文の場合:

Aineq = [1,0,0,-1];
bineq = 0;

溶接部のせん断応力 $τ (x)$ は 13,600 psi を超えることはできません。せん断応力を計算するには、まず予備的な式を計算します。

$τ_{1} = \frac{1}{\sqrt{2} x_{1} x_{2}}$

$R = \sqrt{x_{2}^{2} + (x_{1} + x_{3})^{2}}$

$τ_{2} = \frac{(L + x_{2} / 2) R}{\sqrt{2} x_{1} x_{3} (x_{2}^{2} / 3 + (x_{1} + x_{3})^{2}}$

$τ (x) = P \sqrt{τ_{1}^{2} + τ_{2}^{2} + \frac{2 τ_{1} τ_{2} x_{2}}{R}} .$

要約すると、溶接部のせん断応力には $τ (x)$ <= 13600 という制約があります。

溶接部の通常の応力 $σ (x)$ は 30,000 psi を超えることはできません。通常の応力は $P \frac{6 L}{x_{4} x_{3}^{2}} \leq 30 \times 1 0^{3}$ です。
垂直方向の座屈荷重容量は、適用荷重6,000ポンドを超える必要があります。ヤング率 $E = 30 \times 1 0^{6}$ psiおよび $G = 12 \times 1 0^{6}$ psiの値を使用すると、座屈荷重制約は $\frac{4.013 E x_{3} x_{4}^{3}}{6 L^{2}} (1 - \frac{x_{3}}{2 L} \sqrt{\frac{E}{4 G}}) \geq 6000$ となります。数値的に、これは不等式 $64, 746.022 (1 - 0.0282346 x_{3}) x_{3} x_{4}^{3} \geq 6000$ になります。
変数の境界は 0.125 <=x(1) <= 5, 0.1 <= x(2) <= 10, 0.1 <= x(3) <= 10, 0.125 <= x(4) <= 5 である。ツールボックス構文の場合:

lb = [0.125,0.1,0.1,0.125];
ub = [5,10,10,5];

目的関数は、この例の最後にある関数 objval(x) に表示されます。非線形制約は、この例の最後の関数 nonlcon(x) に表示されます。

多目的問題の定式化と`paretosearch`による解決

この問題を最適化するには、いくつかの方法があります。

最大たわみを設定し、最大たわみ制約を満たす設計にわたって単一目的の最小製造コストを見つけます。
最大製造コストを設定し、製造コストの制約を満たす設計の中で単一目的の最小たわみを見つけます。
2 つの目的間のトレードオフを視覚化して、多目的問題を解決します。

問題についてのより多くの情報を提供する多目的アプローチを使用するには、目的関数と非線形制約関数を設定します。

fun = @objval;
nlcon = @nonlcon;

'psplotparetof' プロット関数で paretosearch を使用して問題を解決します。診断表示情報の量を減らすには、Display オプションを 'off' に設定します。

opts_ps = optimoptions('paretosearch','Display','off','PlotFcn','psplotparetof');
rng default % For reproducibility
[x_ps1,fval_ps1,~,psoutput1] = paretosearch(fun,4,Aineq,bineq,[],[],lb,ub,nlcon,opts_ps);

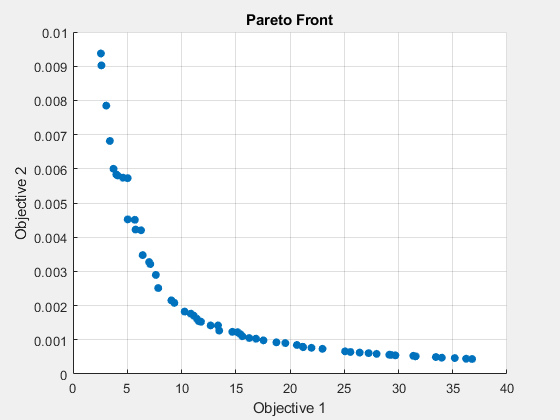
Figure paretosearch contains an axes object. The axes object with title Pareto Front, xlabel Objective 1, ylabel Objective 2 contains an object of type scatter.

disp("Total Function Count: " + psoutput1.funccount);

Total Function Count: 1467

より滑らかなパレートフロントを実現するには、より多くのポイントを使用してみてください。

npts = 160; % The default is 60
opts_ps.ParetoSetSize = npts;
[x_ps2,fval_ps2,~,psoutput2] = paretosearch(fun,4,Aineq,bineq,[],[],lb,ub,nlcon,opts_ps);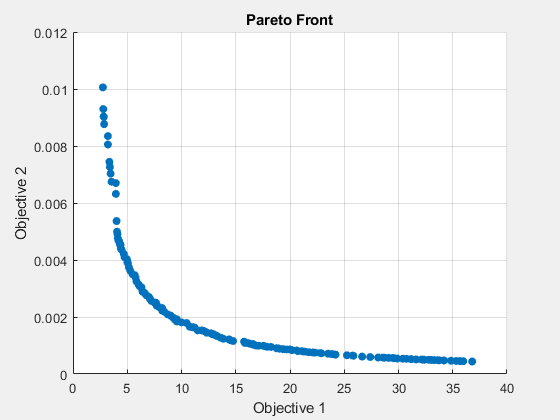

Figure paretosearch contains an axes object. The axes object with title Pareto Front, xlabel Objective 1, ylabel Objective 2 contains an object of type scatter.

disp("Total Function Count: " + psoutput2.funccount);

Total Function Count: 4697

この解決策はより滑らかな曲線のように見えます。60 個ではなく 160 個のパレートポイントを使用すると、ソルバーは 3 倍以上の関数評価を実行します。

`gamultiobj` ソリューション

ソルバーによって違いが出るかどうかを確認するには、問題に gamultiobj ソルバーを試してください。前のソリューションと同じオプションを設定します。gamultiobj ソルバーは、その解の半分未満を最良のパレートフロント上に保持するため、以前の 2 倍のポイントを使用します。

opts_ga = optimoptions('gamultiobj','Display','off','PlotFcn','gaplotpareto','PopulationSize',2*npts);
[x_ga1,fval_ga1,~,gaoutput1] = gamultiobj(fun,4,Aineq,bineq,[],[],lb,ub,nlcon,opts_ga);

Figure Genetic Algorithm contains an axes object. The axes object with title Pareto Front, xlabel Objective 1, ylabel Objective 2 contains an object of type scatter.

disp("Total Function Count: " + gaoutput1.funccount);

Total Function Count: 44161

gamultiobj は数万回の関数評価を必要としますが、paretosearch は数千回しか必要としません。gamultiobj は、特に目的 2 の場合、目的関数値の範囲がわずかに広くなります。

解の比較

gamultiobj ソリューションは paretosearch ソリューションとは異なるように見えますが、プロットされたスケールが異なるため、見分けるのは困難です。同じスケールを使用して、2 つの解を同じプロットにプロットします。

fps2 = sortrows(fval_ps2,1,'ascend');
figure
hold on
plot(fps2(:,1),fps2(:,2),'r-')
fga = sortrows(fval_ga1,1,'ascend');
plot(fga(:,1),fga(:,2),'b--')
xlim([0,40])
ylim([0,1e-2])
legend('paretosearch','gamultiobj')
xlabel 'Cost'
ylabel 'Deflection'
hold off

Figure contains an axes object. The axes object with xlabel Cost, ylabel Deflection contains 2 objects of type line. These objects represent paretosearch, gamultiobj.

paretosearch の解は、プロットの左端の部分ではより優れており、残りの部分では解は区別がつかないように見えます。paretosearch では、解を得るために使用する関数評価の回数がはるかに少なくなります。

通常、問題に非線形制約がない場合、paretosearch は少なくとも gamultiobj と同程度に正確です。ただし、結果として得られるパレート集合の範囲は多少異なる場合があります。

paretosearch の主な利点の 1 つは、通常、関数評価の回数が大幅に減ることです。

単一目的のソリューションから始める

ソルバーがより良いソリューションを見つけられるように、個体の目的関数を最小化するソリューションとなるポイントからソルバーを始めます。pickindex 関数は、objval 関数から単一の目的を返します。fmincon を使用して単一目的の最適値を見つけます。次に、それらのソリューションを多目的探索の初期点として使用します。

x0 = zeros(2,4);
x0f = (lb + ub)/2;
opts_fmc = optimoptions('fmincon','Display','off','MaxFunctionEvaluations',1e4);
x0(1,:) = fmincon(@(x)pickindex(x,1),x0f,Aineq,bineq,[],[],lb,ub,@nonlcon,opts_fmc);
x0(2,:) = fmincon(@(x)pickindex(x,2),x0f,Aineq,bineq,[],[],lb,ub,@nonlcon,opts_fmc);

単一目的最適値を調べます。

objval(x0(1,:))

ans = 1×2

    2.3810    0.0158

objval(x0(2,:))

ans = 1×2

   76.7188    0.0004

最小コストは 2.381 で、偏向は 0.158 になります。最小偏向は 0.0004 で、コストは 76.7188 です。プロットされた曲線は範囲の端の近くでかなり急勾配になっています。これは、コストを最小値より少し上にすると偏向が大幅に少なくなるか、偏向を最小値より少し上にするとコストが大幅に少なくなることを意味します。

単一目的ソリューションから paretosearch を開始します。後で同じプロットに解をプロットするため、paretosearch プロット関数を削除します。

opts_ps.InitialPoints = x0;
opts_ps.PlotFcn = [];
[x_psx0,fval_ps1x0,~,psoutput1x0] = paretosearch(fun,4,Aineq,bineq,[],[],lb,ub,nlcon,opts_ps);
disp("Total Function Count: " + psoutput1x0.funccount);

Total Function Count: 4355

同じ初期点から ga を開始し、そのプロット関数を削除します。

opts_ga.InitialPopulationMatrix = x0;
opts_ga.PlotFcn = [];
[~,fval_ga,~,gaoutput] = gamultiobj(fun,4,Aineq,bineq,[],[],lb,ub,nlcon,opts_ga);
disp("Total Function Count: " + gaoutput.funccount);

Total Function Count: 47361

解を同じ軸上にプロットします。

fps = sortrows(fval_ps1x0,1,'ascend');
figure
hold on
plot(fps(:,1),fps(:,2),'r-')
fga = sortrows(fval_ga,1,'ascend');
plot(fga(:,1),fga(:,2),'b--')
xlim([0,40])
ylim([0,1e-2])
legend('paretosearch','gamultiobj')
xlabel 'Cost'
ylabel 'Deflection'
hold off

Figure contains an axes object. The axes object with xlabel Cost, ylabel Deflection contains 2 objects of type line. These objects represent paretosearch, gamultiobj.

単一目的解から始めると、gamultiobj 解はプロットされた範囲全体にわたって paretosearch 解に類似します。ただし、gamultiobj では、解に到達するまでにほぼ 10 倍の関数評価が必要になります。

ハイブリッド関数

gamultiobj は、ハイブリッド関数fgoalattain を自動的に呼び出して、より正確な解決策を見つけることができます。ハイブリッド関数によってソリューションが改善されるかどうかを確認します。

opts_ga.HybridFcn = 'fgoalattain';
[xgah,fval_gah,~,gaoutputh] = gamultiobj(fun,4,Aineq,bineq,[],[],lb,ub,nlcon,opts_ga);
disp("Total Function Count: " + gaoutputh.funccount);

Total Function Count: 47681

fgah = sortrows(fval_gah,1,'ascend');
figure
hold on
plot(fps(:,1),fps(:,2),'r-')
plot(fga(:,1),fga(:,2),'b--')
plot(fgah(:,1),fgah(:,2),'g-')
xlim([0,40])
ylim([0,1e-2])
legend('paretosearch','gamultiobj','gamultiobj/fgoalattain')
xlabel 'Cost'
ylabel 'Deflection'
hold off

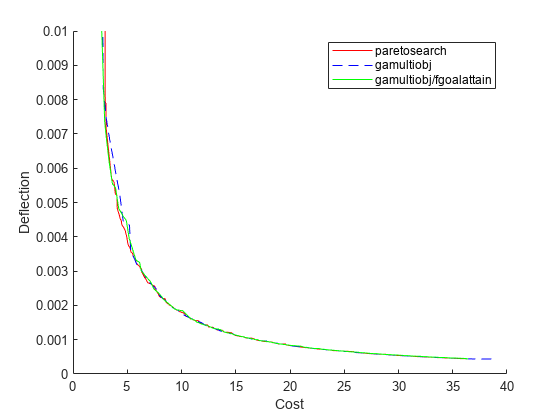
Figure contains an axes object. The axes object with xlabel Cost, ylabel Deflection contains 3 objects of type line. These objects represent paretosearch, gamultiobj, gamultiobj/fgoalattain.

ハイブリッド関数は、主にプロットの左端の部分において、gamultiobj ソリューションにわずかな改善をもたらします。

`paretosearch` ソリューションポイントから `fgoalattain` を手動で実行する

paretosearch にはハイブリッド関数が組み込まれていませんが、paretosearch ソリューションポイントから fgoalattain を実行することで paretosearch ソリューションを改善できます。gamultiobjハイブリッド関数で説明したのと同じ fgoalattain の設定を使用して、fgoalattain の目標と重みを作成します。

Fmax = max(fval_ps1x0);
nobj = numel(Fmax);
Fmin = min(fval_ps1x0);
w = sum((Fmax - fval_ps1x0)./(1 + Fmax - Fmin),2);
p = w.*((Fmax - fval_ps1x0)./(1 + Fmax - Fmin));
xnew = zeros(size(x_psx0));
nsol = size(xnew,1);
fvalnew = zeros(nsol,nobj);
opts_fg = optimoptions('fgoalattain','Display','off');
nfv = 0;
for ii = 1:nsol
    [xnew(ii,:),fvalnew(ii,:),~,~,output] = fgoalattain(fun,x_psx0(ii,:),fval_ps1x0(ii,:),p(ii,:),...
        Aineq,bineq,[],[],lb,ub,nlcon,opts_fg);
    nfv = nfv + output.funcCount;
end
disp("fgoalattain Function Count: " + nfv)

fgoalattain Function Count: 11940

fnew = sortrows(fvalnew,1,'ascend');
figure
hold on
plot(fps(:,1),fps(:,2),'r-')
plot(fga(:,1),fga(:,2),'b--')
plot(fgah(:,1),fgah(:,2),'g-')
plot(fnew(:,1),fnew(:,2),'k.-')
xlim([0,40])
ylim([0,1e-2])
legend('paretosearch','gamultiobj','gamultiobj/fgoalattain','paretosearch/fgoalattain')
xlabel 'Cost'
ylabel 'Deflection'

Figure contains an axes object. The axes object with xlabel Cost, ylabel Deflection contains 4 objects of type line. These objects represent paretosearch, gamultiobj, gamultiobj/fgoalattain, paretosearch/fgoalattain.

paretosearch と fgoalattain の組み合わせにより、最も正確なパレートフロントが作成されます。拡大してご覧ください。

xlim([3.64 13.69])
ylim([0.00121 0.00442])
hold off

追加の fgoalattain 計算があっても、組み合わせの合計関数数は、gamultiobj ソリューションのみの関数数の半分未満になります。

fprintf("Total function count for gamultiobj alone is %d.\n" + ...
    "For paretosearch and fgoalattain together it is %d.\n",...
    gaoutput.funccount,nfv + psoutput1x0.funccount)

Total function count for gamultiobj alone is 47361.
For paretosearch and fgoalattain together it is 16295.

プロットから適切なパラメーターを見つける

プロットされた点は関数空間における最良の値を示しています。どのパラメーターがこれらの関数値を達成するかを決定するには、特定のコスト/たわみポイントを取得できるように、梁のサイズと溶接のサイズを調べます。たとえば、paretosearch の後に fgoalattain が続くプロットは、コストが約 6 で、偏向が約 3.5e–3 のポイントを示しています。これらのポイントを達成する梁と溶接のサイズを決定します。

whichgood = find(fvalnew(:,1) <= 6 & fvalnew(:,2) <= 3.5e-3);
goodpoints = table(xnew(whichgood,:),fvalnew(whichgood,:),'VariableNames',{'Parameters' 'Objectives'})

goodpoints=15×2 table
                   Parameters                       Objectives     
    ________________________________________    ___________________

    0.61638     1.5707         10    0.63173    5.3916    0.0034749
    0.63309     1.5228         10    0.66925    5.6722    0.0032801
    0.47654      2.124         10    0.65248    5.5943    0.0033644
    0.64402     1.4929         10    0.69431    5.8592    0.0031617
     0.6513     1.4736         10    0.71125    5.9854    0.0030864
    0.64938     1.4787         10    0.70676    5.9519     0.003106
    0.61437     1.5767         10    0.62727    5.3582    0.0034996
     0.6157     1.5728         10    0.63022    5.3803    0.0034832
    0.63478     1.5181         10    0.67309    5.7009    0.0032614
    0.64269     1.4965         10    0.69125    5.8364    0.0031757
    0.64144     1.4999         10    0.68835    5.8148    0.0031891
    0.63509     1.5173         10     0.6738    5.7062    0.0032579
    0.65081     1.4749         10    0.71009    5.9768    0.0030914
    0.62551     1.5442         10     0.6521    5.5441    0.0033663
    0.65034     1.4762         10    0.70899    5.9685    0.0030962

いくつかのパラメーターセットでは、コストが6未満、偏向が3.5e–3未満になります。

溶接厚さは0.6をわずかに超える
溶接長さ約1.5
梁の高さ10（上限）
ビーム幅0.63～0.71

客観的制約と非線形制約

function [Cineq,Ceq] = nonlcon(x)
sigma = 5.04e5 ./ (x(:,3).^2 .* x(:,4));
P_c = 64746.022*(1 - 0.028236*x(:,3)).*x(:,3).*x(:,4).^3;
tp = 6e3./sqrt(2)./(x(:,1).*x(:,2));
tpp = 6e3./sqrt(2) .* (14+0.5*x(:,2)).*sqrt(0.25*(x(:,2).^2 + (x(:,1) + x(:,3)).^2)) ./ (x(:,1).*x(:,2).*(x(:,2).^2 / 12 + 0.25*(x(:,1) + x(:,3)).^2));
tau = sqrt(tp.^2 + tpp.^2 + (x(:,2).*tp.*tpp)./sqrt(0.25*(x(:,2).^2 + (x(:,1) + x(:,3)).^2)));
Cineq = [tau - 13600,sigma - 3e4,6e3 - P_c];
Ceq = [];
end

function F = objval(x)
f1 = 1.10471*x(:,1).^2.*x(:,2) + 0.04811*x(:,3).*x(:,4).*(14.0+x(:,2));
f2 = 2.1952./(x(:,3).^3 .* x(:,4));

F = [f1,f2];
end

function z = pickindex(x,k)
    z = objval(x); % evaluate both objectives
    z = z(k); % return objective k
end

参考文献

[1] Deb、Kalyanmoy、J. Sundar、Udaya Bhaskara Rao N、および Shamik Chaudhuri。Reference Point Based Multi-Objective Optimization Using Evolutionary Algorithms.International Journal of Computational Intelligence Research, Vol. 2, No. 3, 2006, pp. 273–286.https://www.softcomputing.net/ijcir/vol2-issu3-paper4.pdf から入手可能です。

[2] Ray, T., and K. M. Liew.A Swarm Metaphor for Multiobjective Design Optimization.Engineering Optimization 34, 2002, pp.141–153.