このページは機械翻訳を使用して翻訳されました。最新版の英語を参照するには、ここをクリックします。

非滑らかな問題に対するソルバーの挙動

この例は、最適化問題に適切なソルバーを選択することの重要性を示しています。また、滑らかでない点が 1 点だけでも、Optimization Toolbox ™ ソルバーに問題を引き起こす可能性があることも示しています。

一般に、ソルバー決定テーブルは、どのソルバーが問題に最も適しているかについてのガイダンスを提供します。滑らかな問題については、最適化の意思決定表を参照してください。滑らかでない問題については、まずソルバー選択表を参照し、詳細については Global Optimization Toolbox ソルバーの特性を参照してください。

滑らかでない点を1つ持つ関数

関数 $f (x) = | | x | |^{1 / 2}$ は、最小点である点 0 では滑らかではありません。以下は、4 次元ポイント $[\begin{array}{cc} x (1) & x (2) \\ 0 & 0 \end{array}]$ の 行列ノルム を使用した 2 次元プロットです。

figure
x = linspace(-5,5,51);
[xx,yy] = meshgrid(x);
zz = zeros(size(xx));
for ii = 1:length(x)
    for jj = 1:length(x)
        zz(ii,jj) = sqrt(norm([xx(ii,jj),yy(ii,jj);0,0]));
    end
end

surf(xx,yy,zz)
xlabel('x(1)')
ylabel('x(2)')
title('Norm([x(1),x(2);0,0])^{1/2}')

Figure contains an axes object. The axes object with title Norm([x( 1 ),x( 2 ); 0 , 0 ]) toThePowerOf 1 / 2 baseline, xlabel x(1), ylabel x(2) contains an object of type surface.

この例では、2 行 6 列の行列 x の行列ノルムを使用します。行列ノルムは、ユークリッドノルムほど滑らかではない特異値分解に関連しています。行列の 2 ノルムを参照してください。

`patternsearch`を使用して最小化

patternsearch は、滑らかでない問題に最初に試すのに推奨されるソルバーです。ソルバー選択表を参照してください。ゼロ以外の 2 行 6 列の行列 x0 から patternsearch を開始し、 $f$ の最小値を見つけようとします。この試行および他のすべての試行では、デフォルトのソルバーオプションを使用します。

ゼロに近い解、同様にゼロに近い目的関数の値、および実行された関数評価の数を返します。

fun = @(x)norm([x(1:6);x(7:12)])^(1/2);
x0 = [1:6;7:12];
rng default
x0 = x0 + rand(size(x0))

x0 = 2×6

    1.8147    2.1270    3.6324    4.2785    5.9575    6.1576
    7.9058    8.9134    9.0975   10.5469   11.9649   12.9706

[xps,fvalps,eflagps,outputps] = patternsearch(fun,x0);

patternsearch stopped because the mesh size was less than options.MeshTolerance.

xps,fvalps,eflagps,outputps.funccount

xps = 2×6
10^-4 ×

    0.1116   -0.1209    0.3503   -0.0520   -0.1270    0.2031
   -0.3082   -0.1526    0.0623    0.0652    0.4479    0.1173

fvalps = 
0.0073

eflagps = 
1

ans = 
10780

patternsearch は、終了フラグ 1 で示されているように、適切な解決策に到達しました。ただし、収束するには 10,000 回を超える関数評価が必要です。

`fminsearch`を使用して最小化

ドキュメントには、fminsearch が不連続性を処理できる場合があると記載されているため、これは合理的なオプションです。

[xfms,fvalfms,eflagfms,outputfms] = fminsearch(fun,x0);

 
Exiting: Maximum number of function evaluations has been exceeded
         - increase MaxFunEvals option.
         Current function value: 3.197063

xfms,fvalfms,eflagfms,outputfms.funcCount

xfms = 2×6

    2.2640    1.1747    9.0693    8.1652    1.7367   -1.2958
    3.7456    1.2694    0.2714   -3.7942    3.8714    1.9290

fvalfms = 
3.1971

eflagfms = 
0

ans = 
2401

デフォルトオプションを使用すると、fminsearch はソリューションに収束する前に関数評価を実行します。終了フラグ 0 は、この収束の欠如を示します。報告された解決策は不十分です。

`particleswarm` を使用する

次に試すべきソルバーとしては、particleswarm が推奨されます。非滑らかな問題に対するソルバーの選択を参照してください。

[xpsw,fvalpsw,eflagpsw,outputpsw] = particleswarm(fun,12);

Optimization ended: relative change in the objective value 
over the last OPTIONS.MaxStallIterations iterations is less than OPTIONS.FunctionTolerance.

xpsw,fvalpsw,eflagpsw,outputpsw.funccount

xpsw = 1×12
10^-12 ×

   -0.0386   -0.1282   -0.0560    0.0904    0.0771   -0.0541   -0.1189    0.1290   -0.0032    0.0165    0.0728   -0.0026

fvalpsw = 
4.5222e-07

eflagpsw = 
1

ans = 
37200

particleswarm は patternsearch よりもさらに正確なソリューションを見つけますが、35,000 回を超える関数評価が必要です。終了フラグ 1 は、ソリューションが適切であることを示します。

`ga` を使用する

ga は人気のあるソルバーですが、最初に試すソルバーとしてはお勧めできません。この問題に対してそれがどれだけうまく機能するか見てみましょう。

[xga,fvalga,eflagga,outputga] = ga(fun,12);

ga stopped because the average change in the fitness value is less than options.FunctionTolerance.

xga,fvalga,eflagga,outputga.funccount

xga = 1×12

   -0.0061   -0.0904    0.0816   -0.0484    0.0799   -0.1925    0.0048    0.3581    0.0848    0.0232    0.0237   -0.1294

fvalga = 
0.6257

eflagga = 
1

ans = 
65190

ga は patternsearch や particleswarm ほど良い解を見つけられず、particleswarm の約 2 倍の関数評価が必要です。この場合、終了フラグ 1 は誤解を招きます。

Optimization Toolbox から `fminunc` を使用する

fminunc は、滑らかでない関数には推奨されません。これでパフォーマンスがどのようになるか見てみましょう。

[xfmu,fvalfmu,eflagfmu,outputfmu] = fminunc(fun,x0);

Local minimum possible.

fminunc stopped because the size of the current step is less than
the value of the step size tolerance.

<stopping criteria details>

xfmu,fvalfmu,eflagfmu,outputfmu.funcCount

xfmu = 2×6

   -0.5844   -0.9726   -0.4356    0.1467    0.3263   -0.1002
   -0.0769   -0.1092   -0.3429   -0.6856   -0.7609   -0.6524

fvalfmu = 
1.1269

eflagfmu = 
2

ans = 
429

fminunc ソリューションは ga ソリューションほど優れていません。しかし、fminunc は、比較的少ない関数評価で、かなり貧弱なソリューションに到達します。終了フラグ 2 は、報告されたソリューションでは 1 次の最適性条件が満たされていないため注意が必要であることを意味します。

Optimization Toolbox から `fmincon` を使用する

fmincon は、滑らかでない関数を最小化できる場合があります。これでパフォーマンスがどのようになるか見てみましょう。

[xfmc,fvalfmc,eflagfmc,outputfmc] = fmincon(fun,x0);

Local minimum possible. Constraints satisfied.

fmincon stopped because the size of the current step is less than
the value of the step size tolerance and constraints are 
satisfied to within the value of the constraint tolerance.

<stopping criteria details>

xfmc,fvalfmc,eflagfmc,outputfmc.funcCount

xfmc = 2×6
10^-9 ×

    0.0435   -0.0976    0.0756   -0.1265    0.0112   -0.0336
    0.0634    0.0528   -0.0144    0.0957    0.1322   -0.1136

fvalfmc = 
1.5501e-05

eflagfmc = 
2

ans = 
876

デフォルトオプションを使用した fmincon は、1000 回未満の関数評価で正確なソリューションを生成します。終了フラグ 2 は、ソリューションが不正確であることを意味するのではなく、1 次の最適性条件が満たされていないことを意味します。これは、目的関数の勾配が解においてゼロではないためです。

結果の要約

適切なソルバーを選択すると、より良い結果がより速く得られます。この要約は、結果がいかに異なる可能性があるかを示しています。目的関数の値が 0.1 より大きい場合、ソリューションの品質は 'Poor' です。値が 0.01 より小さい場合は 'Good'、それ以外の場合は 'Mediocre' です。

Solver = {'patternsearch';'fminsearch';'particleswarm';'ga';'fminunc';'fmincon'};
SolutionQuality = {'Good';'Poor';'Good';'Poor';'Poor';'Good'};
FVal = [fvalps,fvalfms,fvalpsw,fvalga,fvalfmu,fvalfmc]';
NumEval = [outputps.funccount,outputfms.funcCount,outputpsw.funccount,...
    outputga.funccount,outputfmu.funcCount,outputfmc.funcCount]';
results = table(Solver,SolutionQuality,FVal,NumEval)

results=6×4 table
         Solver          SolutionQuality       FVal       NumEval
    _________________    _______________    __________    _______

    {'patternsearch'}       {'Good'}         0.0072656     10780 
    {'fminsearch'   }       {'Poor'}            3.1971      2401 
    {'particleswarm'}       {'Good'}        4.5222e-07     37200 
    {'ga'           }       {'Poor'}           0.62572     65190 
    {'fminunc'      }       {'Poor'}            1.1269       429 
    {'fmincon'      }       {'Good'}        1.5501e-05       876

結果の別のビュー。

figure
hold on
for ii = 1:length(FVal)
    clr = rand(1,3);
    plot(NumEval(ii),FVal(ii),'o','MarkerSize',10,'MarkerEdgeColor',clr,'MarkerFaceColor',clr)
    text(NumEval(ii),FVal(ii)+0.2,Solver{ii},'Color',clr);
end
ylabel('FVal')
xlabel('NumEval')
title('Reported Minimum and Evaluations By Solver')
hold off

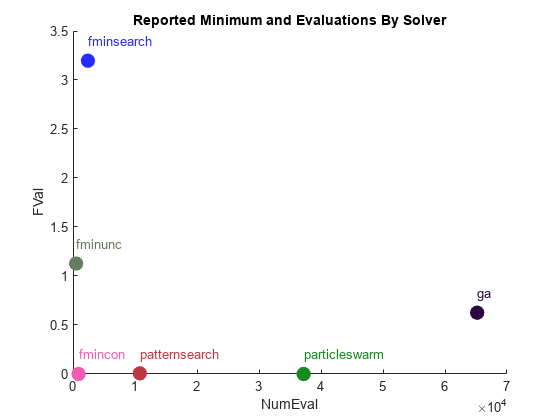
Figure contains an axes object. The axes object with title Reported Minimum and Evaluations By Solver, xlabel NumEval, ylabel FVal contains 12 objects of type line, text. One or more of the lines displays its values using only markers

particleswarm は最も低い目的関数値を達成しますが、そのためには patternsearch の 3 倍以上、fmincon の 30 倍以上の関数評価が必要です。

fmincon は、一般的に、滑らかでない問題には推奨されません。この場合は効果的ですが、この場合には滑らかでない点が 1 つだけあります。

非滑らかな問題に対するソルバーの挙動

滑らかでない点を1つ持つ関数

`patternsearch`を使用して最小化

`fminsearch`を使用して最小化

`particleswarm` を使用する

`ga` を使用する

Optimization Toolbox から `fminunc` を使用する

Optimization Toolbox から `fmincon` を使用する

結果の要約

参考

トピック

非滑らかな問題に対するソルバーの挙動

滑らかでない点を1つ持つ関数

patternsearchを使用して最小化

fminsearchを使用して最小化

particleswarm を使用する

ga を使用する

Optimization Toolbox から fminunc を使用する

Optimization Toolbox から fmincon を使用する

結果の要約

参考

トピック

`patternsearch`を使用して最小化

`fminsearch`を使用して最小化

`particleswarm` を使用する

`ga` を使用する

Optimization Toolbox から `fminunc` を使用する

Optimization Toolbox から `fmincon` を使用する