このページは機械翻訳を使用して翻訳されました。最新版の英語を参照するには、ここをクリックします。
多目的遺伝的アルゴリズムのオプションの効果
この例では、多目的遺伝的アルゴリズムのオプションの効果の一部を示します。optimoptions 関数を使用して、gamultiobj のオプションを作成および変更します。
gamultiobj の問題設定
gamultiobj は、遺伝的アルゴリズムを使用して、複数の目的関数のローカルパレート フロントを検出します。この例では、gamultiobj を使用して、MATLAB ® ファイル kur_multiobjective.m に記述されている 2 つの目的関数のパレート フロントを取得します。このファイルは、それぞれ 3 つの決定変数を持つ 2 つの目的から構成される実数値関数を表します。また、決定変数に境界制約 -5 <= x(i) <= 5、i = 1,2,3 を課します。
type kur_multiobjective.mfunction y = kur_multiobjective(x) %KUR_MULTIOBJECTIVE Objective function for a multiobjective problem. % The Pareto-optimal set for this two-objective problem is nonconvex as % well as disconnected. The function KUR_MULTIOBJECTIVE computes two % objectives and returns a vector y of size 2-by-1. % % Reference: Kalyanmoy Deb, "Multi-Objective Optimization using % Evolutionary Algorithms", John Wiley & Sons ISBN 047187339 % Copyright 2007 The MathWorks, Inc. % Initialize for two objectives y = zeros(2,1); % Compute first objective for i = 1:2 y(1) = y(1) - 10*exp(-0.2*sqrt(x(i)^2 + x(i+1)^2)); end % Compute second objective for i = 1:3 y(2) = y(2) + abs(x(i))^0.8 + 5*sin(x(i)^3); end
ソルバーの進行状況を観察するには、プロット関数 @gaplotpareto を使用して、各世代のパレート フロントをプロットします。optimoptions 関数を使用して、オプションでこのプロット関数を指定します。
FitnessFunction = @kur_multiobjective; % Function handle to the fitness function numberOfVariables = 3; % Number of decision variables lb = [-5 -5 -5]; % Lower bound ub = [5 5 5]; % Upper bound A = []; % No linear inequality constraints b = []; % No linear inequality constraints Aeq = []; % No linear equality constraints beq = []; % No linear equality constraints options = optimoptions(@gamultiobj,'PlotFcn',@gaplotpareto);
gamultiobj ソルバーを実行し、パレート フロント上で見つかった解の数と世代数を表示します。
[x,Fval,exitFlag,Output] = gamultiobj(FitnessFunction,numberOfVariables,A, ...
b,Aeq,beq,lb,ub,options);gamultiobj stopped because the average change in the spread of Pareto solutions is less than options.FunctionTolerance.
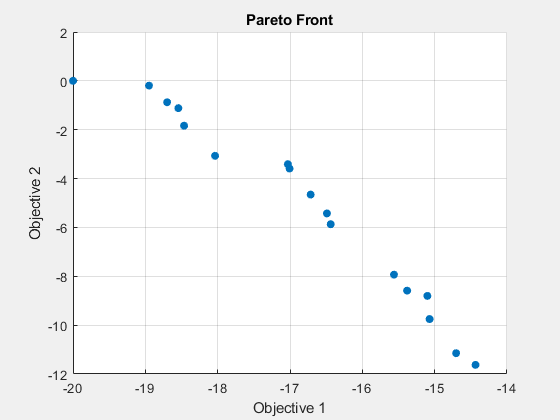
fprintf('The number of points on the Pareto front was: %d\n', size(x,1));The number of points on the Pareto front was: 18
fprintf('The number of generations was : %d\n', Output.generations);The number of generations was : 317
パレート図には、競合する 2 つの目的が表示されます。この問題では、パレート フロントが切断されていることがわかっています。gamultiobj のソリューションでは、パレート フロントが切断されている場合でもそれをキャプチャできます。この例を実行すると、gamultiobj は乱数ジェネレータを使用するため、結果が表示されている結果と異なる場合があることに注意してください。
エリート主義的多目的遺伝的アルゴリズム
多目的遺伝的アルゴリズム (gamultiobj) は、母集団に適用される一連の演算子を使用して母集団に対して作用します。母集団とは、設計空間内の点の集合です。デフォルトでは、初期母集団はランダムに生成されます。母集団の次の世代は、現在の世代の個体の非優位ランクと距離尺度を使用して計算されます。
相対的な適応度を使用して、各個体に非優位ランクが割り当てられます。個体の「p」が「q」よりも優位である(「p」のランクが「q」より低い)のは、少なくとも 1 つの目的において「p」が「q」よりも明らかに優れており、すべての目的において「p」が「q」より劣っていない場合です。これは、「q」が「p」に支配されている、または「p」が「q」より劣っていないと言うのと同じです。2 つの個体「p」と「q」は、どちらも他方を支配していない場合、同等のランクにあるとみなされます。個体の距離測定は、同等のランクの個体を比較するために使用されます。これは、個体が同じランクの他の個体からどれだけ離れているかを測る尺度です。
多目的GA関数gamultiobjは制御されたエリート遺伝的アルゴリズム(NSGA-II [1]の変種)を使用する。エリート主義 GA は常に、適応度値 (ランク) のより高い個体を優先しますが、制御されたエリート主義 GA は、適応度値が低くても母集団の多様性を高めるのに役立つ個体も優先します。最適なパレート フロント最適点に収束するためには、母集団の多様性を維持することが非常に重要です。これは、アルゴリズムが進むにつれて、母集団のエリートメンバーを制御することによって行われます。エリート主義を制御するために、「ParetoFraction」と「DistanceFcn」の 2 つのオプションが使用されます。パレート分数オプションは、パレート フロント上の個体(エリート メンバー) の数を制限し、距離関数はフロント上で比較的遠くにいる個体を優先することでフロント上の多様性を維持するのに役立ちます。
多目的GAオプションの指定
ツールボックスに用意されているデフォルトの距離測定関数 distancecrowding を選択することも、独自の関数を記述して個体の距離測定を計算することもできます。ツールボックスの混雑距離測定関数は、オプションの引数を取り、関数空間 (表現型) または設計空間 (遺伝子型) のいずれかで距離を計算します。'genotype' を選択した場合、パレート フロントの多様性は設計空間に基づきます。デフォルトの選択は 'phenotype' であり、その場合、多様性は関数空間に基づきます。ここでは、距離関数として 'genotype' を選択します。パラメーターDistanceMeasureFcn の値を直接変更します。
options.DistanceMeasureFcn = {@distancecrowding,'genotype'};パレート分数のデフォルト値は 0.35 です。つまり、ソルバーは、現在の母集団内でパレート フロント上にある個体数を母集団サイズの 35 パーセントに制限しようとします。ここではパレート分数を 0.5 に設定します。
options = optimoptions(options,'ParetoFraction',0.5);gamultiobj ソルバーを実行し、パレート フロント上で見つかったソリューションの数とソリューションの平均距離の測定値を表示します。
[x,Fval,exitFlag,Output] = gamultiobj(FitnessFunction,numberOfVariables,A, ...
b,Aeq,beq,lb,ub,options);gamultiobj stopped because the average change in the spread of Pareto solutions is less than options.FunctionTolerance.

fprintf('The number of points on the Pareto front was: %d\n', size(x,1));The number of points on the Pareto front was: 25
fprintf('The average distance measure of the solutions on the Pareto front was: %g\n', Output.averagedistance);The average distance measure of the solutions on the Pareto front was: 0.051005
fprintf('The spread measure of the Pareto front was: %g\n', Output.spread);The spread measure of the Pareto front was: 0.181192
平均距離の測定値が小さいほど、パレート フロント解が均等に分布していることを示します。ただし、パレート フロントが切断されている場合、距離の測定はソリューションの実際の広がりを示しません。
停止基準の変更
gamultiobj は、ソルバーを停止するタイミングを決定するために 3 つの異なる基準を使用します。停止条件のいずれかが満たされると、ソルバーは停止します。最大世代数に達すると停止します。デフォルトではこの数は '200*numberOfVariables' です。gamultiobj は、MaxStallGenerations世代(デフォルトは 100) にわたるパレート フロントの広がりの平均変化が options.FunctionTolerance で指定された許容値より小さい場合にも停止します。3 番目の基準は、秒単位の最大時間制限です (デフォルトは Inf)。ここで、停止基準を変更して、FunctionTolerance を 1e-4 から 1e-3 に変更し、MaxStallGenerations を 150 に増やします。
options = optimoptions(options,'FunctionTolerance',1e-3,'MaxStallGenerations',150);
gamultiobj ソルバーを実行し、パレート フロント上で見つかった解の数と世代数を表示します。
[x,Fval,exitFlag,Output] = gamultiobj(FitnessFunction,numberOfVariables,A, ...
b,Aeq,beq,lb,ub,options);gamultiobj stopped because the average change in the spread of Pareto solutions is less than options.FunctionTolerance.
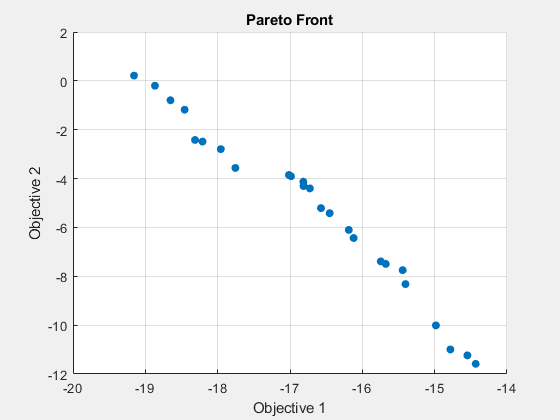
fprintf('The number of points on the Pareto front was: %d\n', size(x,1));The number of points on the Pareto front was: 25
fprintf('The number of generations was : %d\n', Output.generations);The number of generations was : 152
多目的GAハイブリッド関数
多目的問題に最適なパレート フロントを見つけるために、ハイブリッド方式を使用します。gamultiobj は、比較的速く最適なパレート フロントに近い領域に到達できますが、収束に達するまでに多くの関数評価が必要になる場合があります。一般的に使用される手法は、最適なフロントに近づくために少数の世代にわたって gamultiobj を実行することです。次に、gamultiobj からのソリューションは、局所的探索に対してより高速かつ効率的な別の最適化ソルバーの初期点として使用されます。fgoalattain は、gamultiobj とのハイブリッド ソルバーとして使用されます。fgoalattain は、多目的最適化問題を最小化する 1 つの定式化である目標達成問題を解決します。
多目的関数 gamultiobj のハイブリッド機能は、単一目的関数 GA のハイブリッド機能とは少し異なります。単一目的 GA では、ハイブリッド関数はGA によって返された最良のポイントから開始されます。ただし、gamultiobj では、ハイブリッド ソルバーは gamultiobj によって返されるパレート フロント上のすべてのポイントから開始されます。ハイブリッド ソルバーによって返された新しい個体は既存の母集団と結合され、新しいパレート フロントが得られます。fgoalattain 関数の構文を確認すると、gamultiobj 関数の出力が内部的に fgoalattain 関数の入力に変換される仕組みを理解するのに役立つ場合があります。gamultiobj は、パレート フロント上の各ポイントの疑似重み (fgoalattain に必要な入力) を推定し、パレート フロント上の各ポイントからハイブリッド ソルバーを実行します。もう一つの必須入力である goal は、各目的の目標を指定するベクトルです。gamultiobj は、この入力を、これまでに見つかったパレート フロントの極値点として提供します。
ここではハイブリッド関数なしで gamultiobj を実行します。
[x,Fval,exitFlag,Output] = gamultiobj(FitnessFunction,numberOfVariables,A, ...
b,Aeq,beq,lb,ub,options);gamultiobj stopped because the average change in the spread of Pareto solutions is less than options.FunctionTolerance.
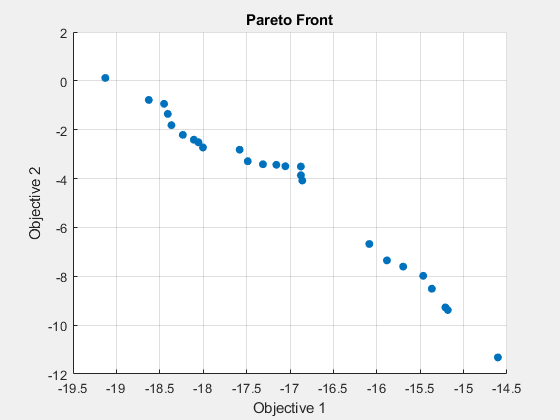
fprintf('The number of points on the Pareto front was: %d\n', size(x,1));The number of points on the Pareto front was: 25
fprintf('The average distance measure of the solutions on the Pareto front was: %g\n', Output.averagedistance);The average distance measure of the solutions on the Pareto front was: 0.0434477
fprintf('The spread measure of the Pareto front was: %g\n', Output.spread);The spread measure of the Pareto front was: 0.17833
ここではハイブリッド関数として fgoalattain を使用します。また、乱数ジェネレーターをリセットして、結果を前回の実行 (ハイブリッド関数なし) と比較できるようにします。
options = optimoptions(options,'HybridFcn',@fgoalattain);ランダム状態をリセットする(前回の実行との比較のみ)
strm = RandStream.getGlobalStream; strm.State = Output.rngstate.State;
ハイブリッド関数を使用して GAMULTIOBJ ソルバーを実行します。
[x,Fval,exitFlag,Output,Population,Score] = gamultiobj(FitnessFunction,numberOfVariables,A, ...
b,Aeq,beq,lb,ub,options);gamultiobj stopped because the average change in the spread of Pareto solutions is less than options.FunctionTolerance.
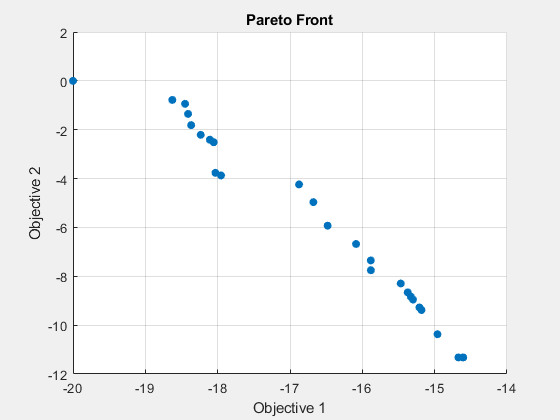
fprintf('The number of points on the Pareto front was: %d\n', size(x,1));The number of points on the Pareto front was: 25
fprintf('The average distance measure of the solutions on the Pareto front was: %g\n', Output.averagedistance);The average distance measure of the solutions on the Pareto front was: 0.128986
fprintf('The spread measure of the Pareto front was: %g\n', Output.spread);The spread measure of the Pareto front was: 0.427487
gamultiobj のみで取得したパレート面とハイブリッド関数を使用して取得したパレート面が近い場合は、広がりと平均距離の尺度を使用して比較できます。パレート フロント解の平均距離は、ハイブリッド関数を使用することで改善できます。広がりは 2 つのフロントにおける変化の尺度であり、ハイブリッド関数を使用すると広がりが高くなる可能性があります。これは、ハイブリッド関数のない gamultiobj によって得られたフロントからフロントが大きく変化したことを示しています。
ハイブリッド関数を使用すると最適なパレート フロントが得られることは確かですが、ソリューションの多様性が失われる可能性があります (fgoalattain は多様性を維持しようとしないため)。これは、平均距離測定値の値がより高いことと、前線の広がりによって示されます。最後の実行で返された最終的な母集団を使用して gamultiobj を再度実行することで、ソリューションの平均距離の測定とパレート フロントの広がりをさらに改善できます。ここで、ハイブリッド関数を削除する必要があります。
options = optimoptions(options,'HybridFcn',[]); % No hybrid function % Provide initial population and scores options = optimoptions(options,'InitialPopulationMatrix',Population,'InitialScoresMatrix',Score); % Run the GAMULTIOBJ solver with hybrid function. [x,Fval,exitFlag,Output,Population,Score] = gamultiobj(FitnessFunction,numberOfVariables,A, ... b,Aeq,beq,lb,ub,options);
gamultiobj stopped because the average change in the spread of Pareto solutions is less than options.FunctionTolerance.
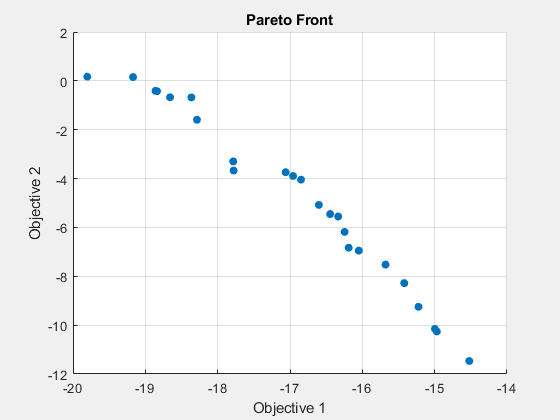
fprintf('The number of points on the Pareto front was: %d\n', size(x,1));The number of points on the Pareto front was: 25
fprintf('The average distance measure of the solutions on the Pareto front was: %g\n', Output.averagedistance);The average distance measure of the solutions on the Pareto front was: 0.0495125
fprintf('The spread measure of the Pareto front was: %g\n', Output.spread);The spread measure of the Pareto front was: 0.169494
参考文献
[1] Kalyanmoy Deb, "Multi-Objective Optimization using Evolutionary Algorithms", John Wiley & Sons ISBN 047187339.