このページは機械翻訳を使用して翻訳されました。最新版の英語を参照するには、ここをクリックします。

遺伝的アルゴリズムを使用したカスタムデータ型の最適化

この例では、遺伝的アルゴリズムを使用して、カスタム データ型を使用して関数を最小化する方法を示します。遺伝的アルゴリズムは巡回セールスマン問題を解決するためにカスタマイズされています。

巡回セールスマン問題

巡回セールスマン問題とは、都市の数が有限で、各都市間の移動コストがわかっている場合の最適化問題です。目標は、コストが最小になるようにセールスマンが訪問するすべての都市の順序付きセットを見つけることです。巡回セールスマン問題を解決するには、都市の位置と、各都市間の距離またはコストのリストが必要です。

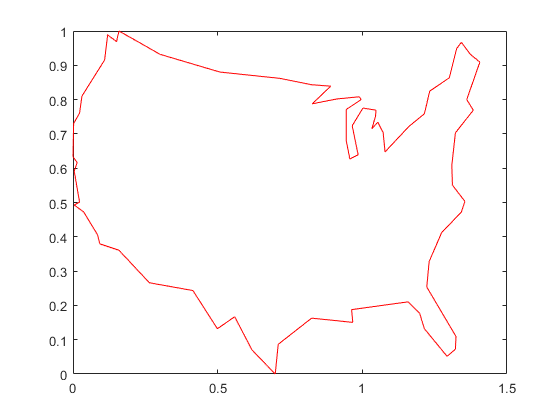
私たちの営業マンはアメリカの都市を訪問しています。ファイル usborder.mat には、変数 x と y に米国の地図が含まれており、変数 xx と yy に同じ地図の幾何学的に簡略化されたバージョンが含まれています。

load('usborder.mat','x','y','xx','yy');
plot(x,y,'Color','red'); hold on;

アメリカ合衆国の国境内にある都市の位置をランダムに生成します。inpolygon 関数を使用すると、すべての都市が米国の境界線内にあるか、非常に近いことを確認できます。

cities = 40;
locations = zeros(cities,2);
n = 1;
while (n <= cities)
    xp = rand*1.5;
    yp = rand;
    if inpolygon(xp,yp,xx,yy)
        locations(n,1) = xp;
        locations(n,2) = yp;
        n = n+1;
    end
end
plot(locations(:,1),locations(:,2),'bo');

青い円は、営業担当者が商品を配達または受け取るために出張する必要がある都市の位置を表しています。都市の場所のリストが与えられれば、すべての都市の距離行列を計算できます。

distances = zeros(cities);
for count1=1:cities,
    for count2=1:count1,
        x1 = locations(count1,1);
        y1 = locations(count1,2);
        x2 = locations(count2,1);
        y2 = locations(count2,2);
        distances(count1,count2)=sqrt((x1-x2)^2+(y1-y2)^2);
        distances(count2,count1)=distances(count1,count2);
    end;
end;

カスタムデータ型向けに遺伝的アルゴリズムをカスタマイズする

デフォルトでは、遺伝的アルゴリズム ソルバーは、double およびバイナリ文字列データ型に基づいて最適化問題を解決します。作成、交叉、突然変異の関数では、母集団が double 型の行列、またはバイナリ文字列の場合は論理型の行列であると想定されます。遺伝的アルゴリズム ソルバーは、任意のデータ型を含む最適化問題にも使用できます。母集団には任意のデータ構造を使用できます。たとえば、MATLAB ® セル配列を使用してカスタム データ型を指定できます。ga をセル配列型の母集団で使用するには、セル配列などのデータ タイプで機能する作成関数、交叉関数、および突然変異関数を提供する必要があります。

巡回セールスマン問題に必要な関数

このセクションでは、必要な 3 つの関数を作成して登録する方法を示します。巡回セールスマン問題の母集団内の個体は順序付けられた集合であるため、母集団はセル配列を使用して簡単に表すことができます。巡回セールスマン問題のカスタム作成関数は、P などのセル配列を作成します。ここで、各要素は順列ベクトルとして順序付けられた都市のセットを表します。つまり、セールスマンは P{i} で指定された順序で移動することになります。作成関数は、サイズが PopulationSize のセル配列を返します。

type create_permutations.m

function pop = create_permutations(NVARS,FitnessFcn,options)
%CREATE_PERMUTATIONS Creates a population of permutations.
%   POP = CREATE_PERMUTATION(NVARS,FITNESSFCN,OPTIONS) creates a population
%  of permutations POP each with a length of NVARS. 
%
%   The arguments to the function are 
%     NVARS: Number of variables 
%     FITNESSFCN: Fitness function 
%     OPTIONS: Options structure used by the GA

%   Copyright 2004-2007 The MathWorks, Inc.

totalPopulationSize = sum(options.PopulationSize);
n = NVARS;
pop = cell(totalPopulationSize,1);
for i = 1:totalPopulationSize
    pop{i} = randperm(n); 
end

カスタム交叉関数は、セル配列(母集団)を受け取り、交叉の結果生じた子であるセル配列を返します。

type crossover_permutation.m

function xoverKids  = crossover_permutation(parents,options,NVARS, ...
    FitnessFcn,thisScore,thisPopulation)
%   CROSSOVER_PERMUTATION Custom crossover function for traveling salesman.
%   XOVERKIDS = CROSSOVER_PERMUTATION(PARENTS,OPTIONS,NVARS, ...
%   FITNESSFCN,THISSCORE,THISPOPULATION) crossovers PARENTS to produce
%   the children XOVERKIDS.
%
%   The arguments to the function are 
%     PARENTS: Parents chosen by the selection function
%     OPTIONS: Options created from OPTIMOPTIONS
%     NVARS: Number of variables 
%     FITNESSFCN: Fitness function 
%     STATE: State structure used by the GA solver 
%     THISSCORE: Vector of scores of the current population 
%     THISPOPULATION: Matrix of individuals in the current population

%   Copyright 2004-2015 The MathWorks, Inc. 

nKids = length(parents)/2;
xoverKids = cell(nKids,1); % Normally zeros(nKids,NVARS);
index = 1;

for i=1:nKids
    % here is where the special knowledge that the population is a cell
    % array is used. Normally, this would be thisPopulation(parents(index),:);
    parent = thisPopulation{parents(index)};
    index = index + 2;

    % Flip a section of parent1.
    p1 = ceil((length(parent) -1) * rand);
    p2 = p1 + ceil((length(parent) - p1- 1) * rand);
    child = parent;
    child(p1:p2) = fliplr(child(p1:p2));
    xoverKids{i} = child; % Normally, xoverKids(i,:);
end

カスタム突然変異関数は、都市の順序付けられたセットである個体を受け取り、変異した順序付けられたセットを返します。

type mutate_permutation.m

function mutationChildren = mutate_permutation(parents ,options,NVARS, ...
    FitnessFcn, state, thisScore,thisPopulation,mutationRate)
%   MUTATE_PERMUTATION Custom mutation function for traveling salesman.
%   MUTATIONCHILDREN = MUTATE_PERMUTATION(PARENTS,OPTIONS,NVARS, ...
%   FITNESSFCN,STATE,THISSCORE,THISPOPULATION,MUTATIONRATE) mutate the
%   PARENTS to produce mutated children MUTATIONCHILDREN.
%
%   The arguments to the function are 
%     PARENTS: Parents chosen by the selection function
%     OPTIONS: Options created from OPTIMOPTIONS
%     NVARS: Number of variables 
%     FITNESSFCN: Fitness function 
%     STATE: State structure used by the GA solver 
%     THISSCORE: Vector of scores of the current population 
%     THISPOPULATION: Matrix of individuals in the current population
%     MUTATIONRATE: Rate of mutation

%   Copyright 2004-2015 The MathWorks, Inc.

% Here we swap two elements of the permutation
mutationChildren = cell(length(parents),1);% Normally zeros(length(parents),NVARS);
for i=1:length(parents)
    parent = thisPopulation{parents(i)}; % Normally thisPopulation(parents(i),:)
    p = ceil(length(parent) * rand(1,2));
    child = parent;
    child(p(1)) = parent(p(2));
    child(p(2)) = parent(p(1));
    mutationChildren{i} = child; % Normally mutationChildren(i,:)
end

巡回セールスマン問題には適応度関数も必要です。個体の適応度は、順序付けられた都市の集合における移動距離の合計です。適応度関数では、合計距離を計算するために距離行列も必要です。

type traveling_salesman_fitness.m

function scores = traveling_salesman_fitness(x,distances)
%TRAVELING_SALESMAN_FITNESS  Custom fitness function for TSP. 
%   SCORES = TRAVELING_SALESMAN_FITNESS(X,DISTANCES) Calculate the fitness 
%   of an individual. The fitness is the total distance traveled for an
%   ordered set of cities in X. DISTANCE(A,B) is the distance from the city
%   A to the city B.

%   Copyright 2004-2007 The MathWorks, Inc.

scores = zeros(size(x,1),1);
for j = 1:size(x,1)
    % here is where the special knowledge that the population is a cell
    % array is used. Normally, this would be pop(j,:);
    p = x{j}; 
    f = distances(p(end),p(1));
    for i = 2:length(p)
        f = f + distances(p(i-1),p(i));
    end
    scores(j) = f;
end

ga は、引数 x のみを使用して適応度関数を呼び出しますが、適応度関数には引数 x、distances の 2 つがあります。匿名関数を使用して、追加の引数である距離行列の値を取得できます。1 つの入力 x を受け取り、x と距離を使用して traveling_salesman_fitness を呼び出す匿名関数への関数ハンドル FitnessFcn を作成します。関数ハンドル FitnessFcn が作成されると、変数 distances に値が含まれるため、これらの値は匿名関数によってキャプチャされます。

%distances defined earlier
FitnessFcn = @(x) traveling_salesman_fitness(x,distances);

都市の位置と現在の最適なルートをプロットするためのカスタム プロット関数を追加できます。赤い円は都市を表し、青い線は 2 つの都市間の有効な経路を表します。

type traveling_salesman_plot.m

function state = traveling_salesman_plot(options,state,flag,locations)
%   TRAVELING_SALESMAN_PLOT Custom plot function for traveling salesman.
%   STATE = TRAVELING_SALESMAN_PLOT(OPTIONS,STATE,FLAG,LOCATIONS) Plot city
%   LOCATIONS and connecting route between them. This function is specific
%   to the traveling salesman problem.

%   Copyright 2004-2006 The MathWorks, Inc.
persistent x y xx yy
if strcmpi(flag,'init')
  load('usborder.mat','x','y','xx','yy');
end
plot(x,y,'Color','red');
axis([-0.1 1.5 -0.2 1.2]);

hold on;
[unused,i] = min(state.Score);
genotype = state.Population{i};

plot(locations(:,1),locations(:,2),'bo');
plot(locations(genotype,1),locations(genotype,2));
hold off

ここでも匿名関数を使用して、追加の引数 locations を指定して traveling_salesman_plot を呼び出す匿名関数への関数ハンドルを作成します。

%locations defined earlier
my_plot = @(options,state,flag) traveling_salesman_plot(options, ...
    state,flag,locations);

遺伝的アルゴリズムのオプション設定

まず、カスタム データ型と母集団範囲を示すオプション コンテナーを作成します。

options = optimoptions(@ga, 'PopulationType', 'custom','InitialPopulationRange', ...
                            [1;cities]);

作成したカスタムの作成、交叉、突然変異、プロット関数を選択し、いくつかの停止条件も設定します。

options = optimoptions(options,'CreationFcn',@create_permutations, ...
                        'CrossoverFcn',@crossover_permutation, ...
                        'MutationFcn',@mutate_permutation, ...
                        'PlotFcn', my_plot, ...
                        'MaxGenerations',500,'PopulationSize',60, ...
                        'MaxStallGenerations',200,'UseVectorized',true);

最後に、問題情報を使用して遺伝的アルゴリズムを呼び出します。

numberOfVariables = cities;
[x,fval,reason,output] = ...
    ga(FitnessFcn,numberOfVariables,[],[],[],[],[],[],[],options)

ga stopped because it exceeded options.MaxGenerations.

x =

  1×1 cell array

    {[14 12 36 3 5 11 40 25 38 37 7 30 28 10 23 21 27 4 1 29 … ] (1×40 double)}


fval =

    5.3846


reason =

     0


output = 

  struct with fields:

      problemtype: 'unconstrained'
         rngstate: [1×1 struct]
      generations: 500
        funccount: 28563
          message: 'ga stopped because it exceeded options.MaxGenerations.'
    maxconstraint: []
       hybridflag: []

この図には、青い円で囲まれた都市の位置と、遺伝的アルゴリズムによって発見されたセールスマンが移動する経路が表示されます。セールスマンはルートのどちらの端からでも出発することができ、最後に出発都市に戻って帰宅することができます。

参考

トピック

• 巡回セールスマン問題: ソルバーベース