ハードウェア効率に優れた Real Partial-Systolic Matrix Solve Using QR Decomposition の対角ローディングによる実装
この例では、次の実数値の行列方程式に対するハードウェア効率に優れた最小二乗解を実装する方法を示します。
![$$\left[\begin{array}{c}\lambda I\\A\end{array}\right] X = \left[\begin{array}{c}O\\B\end{array}\right]$$](../../examples/fixedpoint/win64/RealPartialSystolicQRDiagonalLoadingMatrixSolveExample_eq13421924873373409154.png)
ここでは Real Partial-Systolic Matrix Solve Using QR Decomposition ブロックを使用します。このメソッドは対角ローディングと呼ばれ、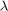 は正則化パラメーターと呼ばれます。
は正則化パラメーターと呼ばれます。
対角ローディング メソッド
Real Partial-Systolic Matrix Solve Using QR Decomposition ブロックで正則化パラメーターを非ゼロの値に設定すると、ブロックは次の最小二乗解を計算します。
![$$\left[\begin{array}{c}\lambda I\\A\end{array}\right] X = \left[\begin{array}{c}O\\B\end{array}\right]$$](../../examples/fixedpoint/win64/RealPartialSystolicQRDiagonalLoadingMatrixSolveExample_eq13421924873373409154.png)
ここで、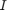 は n 行 n 列の単位行列、
は n 行 n 列の単位行列、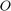 はサイズが n 行 p 列のゼロの配列です。
はサイズが n 行 p 列のゼロの配列です。
このメソッドは対角ローディングと呼ばれ、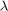 は正則化パラメーターと呼ばれます。この方程式の最小二乗解について、教科書では一般に次のように記載されています。これは、方程式の両辺に
は正則化パラメーターと呼ばれます。この方程式の最小二乗解について、教科書では一般に次のように記載されています。これは、方程式の両辺に ![$[\lambda I,\; A']$](../../examples/fixedpoint/win64/RealPartialSystolicQRDiagonalLoadingMatrixSolveExample_eq17713795801863575823.png) を乗算し、左辺で逆行列を取ることによって導出されます。
を乗算し、左辺で逆行列を取ることによって導出されます。
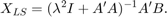
Real Partial-Systolic Matrix Solve Using QR Decomposition ブロックは、逆数を計算する代わりに QR 分解を計算することで効率的に解を計算します。
![$$\left[\begin{array}{c}\lambda I\\A\end{array}\right]$$](../../examples/fixedpoint/win64/RealPartialSystolicQRDiagonalLoadingMatrixSolveExample_eq04204039264175687888.png)
上記をインプレースで上三角 R に変換します。
![$$\left[\begin{array}{c}O\\B\end{array}\right]$$](../../examples/fixedpoint/win64/RealPartialSystolicQRDiagonalLoadingMatrixSolveExample_eq15030873216691328927.png)
上記をインプレースで次のように変換します。
![$$C = Q'\left[\begin{array}{c}O\\B\end{array}\right]$$](../../examples/fixedpoint/win64/RealPartialSystolicQRDiagonalLoadingMatrixSolveExample_eq17485136644078923159.png)
変換した方程式 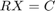 を解きます。
を解きます。
行列の次元の定義
行列 A と B の行数、行列 A の列数、および行列 B の列数を指定します。
m = 300; % Number of rows in matrices A and B n = 10; % Number of columns in matrix A p = 1; % Number of columns in matrix B
正則化パラメーターの定義
Real Partial-Systolic Matrix Solve Using QR Decomposition ブロックで正則化パラメーターが非ゼロの場合、対角ローディング メソッドが使用されます。正則化パラメーターがゼロの場合、方程式は最小二乗の通常の式 AX=B になります。
regularizationParameter = 1e-3;
ブロック パラメーター
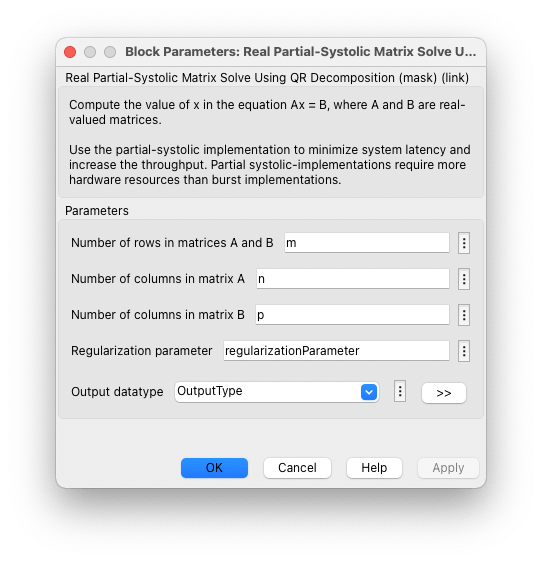
乱数の最小二乗行列の生成
この例では、補助関数 realRandomLeastSquaresMatrices を使用して、最小二乗問題 AX=B の乱数行列 A と B を生成します。生成される行列について、A と B の要素は -1 ~ +1、A のランクは r とします。
rng('default') r = 3; % Rank of matrix A [A,B] = fixed.example.realRandomLeastSquaresMatrices(m,n,p,r);
固定小数点データ型の選択
補助関数 realQRMatrixSolveFixedpointTypes を使用して、入力行列 A と B、および出力 X に対して、計算時のオーバーフローの可能性が低くなる固定小数点データ型を選択します。
max_abs_A = 1; % Upper bound on max(abs(A(:)) max_abs_B = 1; % Upper bound on max(abs(B(:)) precisionBits = 24; % Number of bits of precision T = fixed.realQRMatrixSolveFixedpointTypes(m,n,max_abs_A,max_abs_B,precisionBits); A = cast(A,'like',T.A); B = cast(B,'like',T.B); OutputType = fixed.extractNumericType(T.X);
モデルを開く
model = 'RealPartialSystolicQRDiagonalLoadingMatrixSolveModel';
open_system(model);
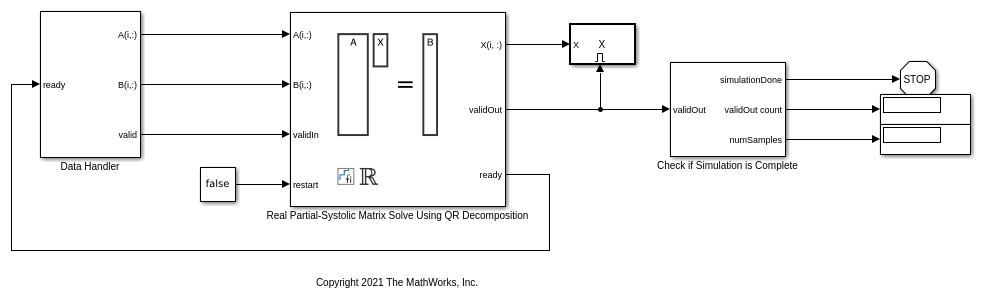
このモデルの Data Handler サブシステムは、実数行列 A と B を入力として取ります。Data Handler は ready 端子によってトリガーされます。true の validIn 信号を送信してから、ready が false に設定されるまでに、多少の遅延が生じることがあります。Data Handler が ready 信号の立ち上がりエッジを検出すると、ブロックは validIn を true に設定し、A と B の次の行を送信します。このプロトコルにより、ready 信号の立ち上がりエッジが検出されるたびにデータが送信され、すべてのデータが確実に処理されます。
モデル ワークスペースの変数の設定
補助関数 setModelWorkspace を使用して、上記で定義された変数をモデル ワークスペースに追加します。これらの変数は、Real Partial-Systolic Matrix Solve Using QR Decomposition ブロックのブロック パラメーターに対応します。
numSamples = 1; % Number of sample matrices fixed.example.setModelWorkspace(model,'A',A,'B',B,'m',m,'n',n,'p',p,... 'regularizationParameter',regularizationParameter,... 'numSamples',numSamples,'OutputType',OutputType);
モデルのシミュレーション
out = sim(model);
出力データからの解の構成
Real Partial-Systolic Matrix Solve Using QR Decomposition ブロックは一度に 1 行ずつデータを出力します。結果の行が出力されると、ブロックは validOut を true に設定します。X の行は計算された順に最後の行から出力されるため、結果を解釈するにはデータを再構成しなければなりません。出力データから行列 X を再構成するには、補助関数 matrixSolveModelOutputToArray を使用します。
X = fixed.example.matrixSolveModelOutputToArray(out.X,n,p,numSamples);
出力の精度の検証
Real Partial-Systolic Matrix Solve Using QR Decomposition ブロックの精度を評価するには、相対誤差を計算します。
A_lambda = [regularizationParameter * eye(n);A];
B_0 = [zeros(n,p);B];
relative_error = norm(double(A_lambda*X - B_0))/norm(double(B_0)) %#ok<NOPTS>
relative_error = 1.2199e-04
参考
ツール
ブロック
トピック
- ハードウェア効率に優れた Real Partial-Systolic Matrix Solve Using QR Decomposition の実装
- ハードウェア効率に優れた、Tikhonov 正則化を使用した Real Partial-Systolic Matrix Solve Using QR Decomposition の実装
- Algorithms to Determine Fixed-Point Types for Real Least-Squares Matrix Solve AX=B
- Determine Fixed-Point Types for Real Least-Squares Matrix Solve AX=B
- Tikhonov 正則化を使用した実数最小二乗行列解の固定小数点型の判別