ハードウェア効率に優れた Real Partial-Systolic Matrix Solve Using Q-less QR Decomposition の実装
この例では、Real Partial-Systolic Matrix Solve Using Q-less QR Decomposition ブロックを使用して、実数値の行列方程式 A'AX=B に対するハードウェア効率に優れた解を実装する方法を示します。
前進代入と後退代入
上三角因子の準備が整うと、前進代入と後退代入が現在の入力 B で計算され、出力 X が生成されます。
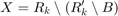
行列の次元の定義
行列 A の行数、行列 A の列数と行列 B の行数、および行列 B の列数を指定します。
m = 30; % Number of rows in A n = 10; % Number of columns in A and rows in B p = 1; % Number of columns in B numInputs = 3; % Number of A and B matricies
行列の生成
この例では、補助関数 realRandomQlessQRMatrices を使用して、問題 A'AX=B の乱数行列 A と B を生成します。生成される行列について、A と B の要素は -1 ~ +1、A のランクはフル ランクとします。
rng('default') [A,B] = fixed.example.realRandomQlessQRMatrices(m,n,p); if numInputs > 1 for i = 2:numInputs [Atemp,Btemp] = fixed.example.realRandomQlessQRMatrices(m,n,p); A = cat(3,A,Atemp); B = cat(3,B,Btemp); end end
固定小数点データ型の選択
補助関数 realQlessQRMatrixSolveFixedpointTypes を使用して、入力行列 A と B、および出力 X に対して、計算時のオーバーフローの可能性が低くなる固定小数点データ型を選択します。
max_abs_A = 1; % Upper bound on max(abs(A(:)) max_abs_B = 1; % Upper bound on max(abs(B(:)) precisionBits = 24; % Number of bits of precision T = fixed.realQlessQRMatrixSolveFixedpointTypes(m,n,max_abs_A,max_abs_B,precisionBits); A = cast(A,'like',T.A); B = cast(B,'like',T.B); OutputType = fixed.extractNumericType(T.X);
モデルを開く
model = 'RealPartialSystolicQlessQRMatrixSolveModel';
open_system(model);
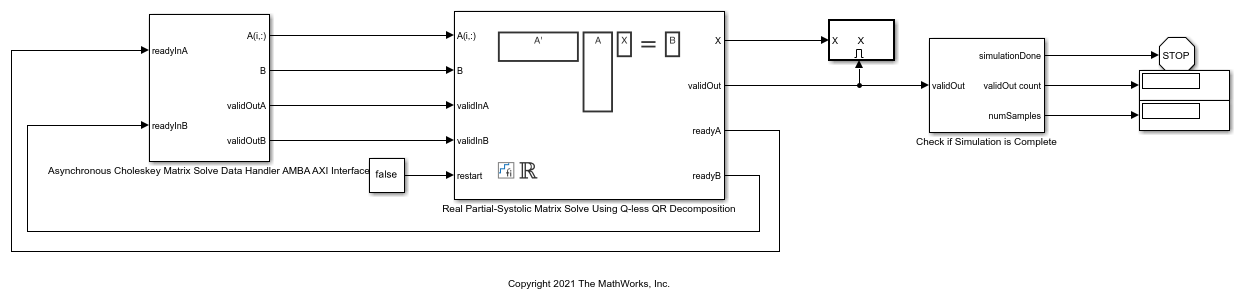
AMBA AXI ハンドシェーキング プロセス
このモデルの Data Handler サブシステムは、実数行列 A と B を入力として取ります。A の行と B の完全な行列を AMBA AXI ハンドシェイク プロトコルを使用して QR Decomposition ブロックに送ります。validIn 信号はデータが使用可能であることを示します。ready 信号はブロックでデータを受け入れ可能であることを示します。validIn 信号と ready 信号の両方が High の場合にのみデータの転送が行われます。Data Handler に A の行が送られるまでの遅延と B の行列が送られるまでの遅延を設定して、上流のブロックの処理時間をエミュレートできます。aDelay と bDelay が 0 に設定されているときは、Data Handler に使用可能なデータが常にあることを示すため、validInA と validInB は High のままになります。A と B のすべての行列が送られると、Data Handler は A と B の最初の行列にループバックします。
非同期の行列ソルバー
このブロックは非同期的に動作します。まず、入力行列 A の Q-less QR 分解が実行され、結果の行列 R がバッファーに格納されます。次に、Forward Backward Substitute ブロックで、入力行列 B とバッファーに格納された行列 R を使用して R'RX = B が計算されます。行列 R と行列 B がバッファーに別々に格納されるため、上流の Q-less QR Decomposition ブロックと下流の Forward Backward Substitute ブロックを独立して実行できます。Forward Backward Substitute ブロックによる処理は、1 つ目の行列 R と B が使用できるようになると開始されます。その後、Q-less QR Decomposition ブロックのステータスに関係なく、バッファーに格納された最新の行列 R と B を使用して連続的に実行されます。たとえば、上流のブロックからの行列 A と B の提供が停止すると、Forward Backward Substitute ブロックは行列 R と B の最後のペアを使用して同じ出力を生成し続けます。
Data Handler は、行列 A と B を QR Decomposition ブロックに反復的に送ります。最後の行列 A を送った後、Data Handler は内部のカウンターをリセットし、最初の行列 A を送ります。行列 B も同じように扱われます。
モデル ワークスペースの変数の設定
補助関数 setModelWorkspace を使用して、上記で定義された変数をモデル ワークスペースに追加します。これらの変数は、Real Partial-Systolic Matrix Solve Using Q-less QR Decomposition ブロックのブロック パラメーターに対応します。
numOutputs = 10; % Number of recorded outputs aDelay = 1; % Delay of clock cycles between feeding in rows of A bDelay = 1; % Delay of clock cycles between feeding in B matrices fixed.example.setModelWorkspace(model,'A',A,'B',B,'m',m,'n',n,'p',p,... 'regularizationParameter',0,... 'aDelay',aDelay,'bDelay',bDelay,... 'numOutputs',numOutputs,'OutputType',OutputType);
モデルのシミュレーション
out = sim(model);
出力データからの解の構成
Real Partial-Systolic Matrix Solve Using Q-less QR Decomposition ブロックは、各タイム ステップで行列 X を出力します。有効な結果の行列が出力されると、ブロックは validOut を true に設定します。
X = out.X;
出力の精度の検証
Real Partial-Systolic Matrix Solve Using Q-less QR Decomposition ブロックの精度を評価するには、相対誤差を計算します。シミュレーションの最後の出力を選択します。
X = double(X(:,:,end));
最後の出力 X を生成した入力 A と B を見つけて、その出力を入力と同期します。
A = double(A); B = double(B); relative_errors = zeros(size(A,3),size(B,3)); for k = 1:size(A,3) for g = 1:size(B,3) relative_errors(k,g) = norm(A(:,:,k)'*A(:,:,k)*X - B(:,:,g))/norm(B(:,:,g)); end end [AUsed,Bused] = find(relative_errors==min(relative_errors,[],'all')) %#ok<NOPTS> relative_error = norm(double(A(:,:,AUsed)'*A(:,:,AUsed)*X - B(:,:,Bused)))/norm(double(B(:,:,Bused))) %#ok<NOPTS>
AUsed =
3
Bused =
2
relative_error =
8.2414e-05