ハードウェア効率に優れた、Tikhonov 正則化を使用した Complex Partial-Systolic Matrix Solve Using QR Decomposition の実装

スクリプトを開く

この例では、Complex Partial-Systolic Matrix Solve Using QR Decomposition ブロックを使用して、次に示す正則化された最小二乗行列方程式を解く方法を説明します。

$\left[\begin{array}{c}\lambda I_n\\A\end{array}\right]X =
\left[\begin{array}{c}0_{n,p}\\B\end{array}\right],$

ここで、A は m 行 n 列の行列 (m >= n)、B は m 行 p 列、X は n 行 p 列、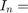 eye(n)、 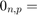$0_{n,p}=$ zeros(n,p)、 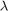$\lambda$ は正則化パラメーターです。

最小二乗解は次のとおりです。

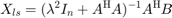
$X_{ls} = (\lambda^2I_n + A^\mathrm{H}A)^{-1}A^\mathrm{H}B$

ただし、二乗や逆数を使用せずに計算されます。

行列の次元の定義

行列 A と B の行数、行列 A の列数、および行列 B の列数を指定します。

m = 100; % Number of rows in matrices A and B
n = 10;  % Number of columns in matrix A
p = 1;   % Number of columns in matrix B

Tikhonov 正則化パラメーターの定義

正則化パラメーターを小さい正の値にすると、問題の調整を向上させ、推定値の分散を小さくすることができます。バイアスがありますが、推定値の分散が小さいと、多くの場合、最小二乗推定値と比べて平均二乗誤差が小さくなります。

regularizationParameter = 0.01;

乱数の最小二乗行列の生成

この例では、補助関数 complexRandomLeastSquaresMatrices を使用して、最小二乗問題 AX=B の乱数行列 A と B を生成します。生成される行列について、A と B の要素の実数部と虚数部は -1 ～ +1、A のランクは r とします。

rng('default')
r = 3;  % Rank of A
[A,B] = fixed.example.complexRandomLeastSquaresMatrices(m,n,p,r);

固定小数点データ型の選択

補助関数 complexQRMatrixSolveFixedpointTypes を使用して、入力行列 A と B、および出力 X に対して、計算時のオーバーフローの可能性が低くなる固定小数点データ型を選択します。

A と B の要素の実数部と虚数部は -1 ～ 1 であるため、任意の要素が取りうる最大絶対値は sqrt(2) です。

max_abs_A = sqrt(2);  % Upper bound on max(abs(A(:))
max_abs_B = sqrt(2);  % Upper bound on max(abs(B(:))
precisionBits = 32;   % Number of bits of precision
T = fixed.complexQRMatrixSolveFixedpointTypes(m,n,max_abs_A,max_abs_B,...
    precisionBits,[],[],regularizationParameter);
A = cast(A,'like',T.A);
B = cast(B,'like',T.B);
OutputType = fixed.extractNumericType(T.X);

モデルを開く

model = 'ComplexPartialSystolicQRMatrixSolveModel';
open_system(model);

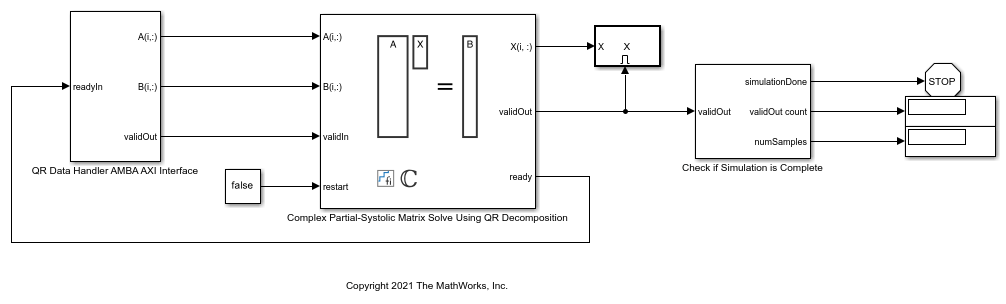
このモデルの Data Handler サブシステムは、複素行列 A と B を入力として取ります。A と B の行を AMBA AXI ハンドシェイクプロトコルを使用して QR ブロックに送ります。validIn 信号はデータが使用可能であることを示します。ready 信号はブロックでデータを受け入れ可能であることを示します。validIn 信号と ready 信号の両方が High の場合にのみデータの転送が行われます。Data Handler に A の行が送られてから B の行が送られるまでの遅延を設定して、上流のブロックの処理時間をエミュレートできます。rowDelay が 0 に設定されているときは、Data Handler に使用可能なデータが常にあることを示すため、validIn は High のままになります。

モデルワークスペースの変数の設定

補助関数 setModelWorkspace を使用して、上記で定義された変数をモデルワークスペースに追加します。これらの変数は、Complex Partial-Systolic Matrix Solve Using QR Decomposition ブロックのブロックパラメーターに対応します。

numSamples = 1; % Number of sample matrices
rowDelay = 1; % Delay of clock cycles between feeding in rows of A and B
fixed.example.setModelWorkspace(model,'A',A,'B',B,'m',m,'n',n,'p',p,...
    'regularizationParameter',regularizationParameter,...
    'numSamples',numSamples,'rowDelay',rowDelay,'OutputType',OutputType);

モデルのシミュレーション

out = sim(model);

出力データからの解の構成

Complex Partial-Systolic Matrix Solve Using QR Decomposition ブロックは一度に 1 行ずつデータを出力します。結果の行が出力されると、ブロックは validOut を true に設定します。X の行は計算された順に最後の行から出力されるため、結果を解釈するにはデータを再構成しなければなりません。出力データから行列 X を再構成するには、補助関数 matrixSolveModelOutputToArray を使用します。

X = fixed.example.matrixSolveModelOutputToArray(out.X,n,p,numSamples);

出力の精度の検証

倍精度浮動小数点において、固定小数点出力と組み込み MATLAB 関数間の相対誤差が小さいことを確認します。

$X_\textrm{double} = \left[\begin{array}{c}\lambda I_n\\A\end{array}\right] \backslash
\left[\begin{array}{c}0_{n,p}\\B\end{array}\right]$

A_lambda = double([regularizationParameter*eye(n);A]);
B_0 = [zeros(n,p);double(B)];
X_double = A_lambda\B_0;
relativeError = norm(X_double - double(X))/norm(X_double)