ハードウェア効率に優れた、Tikhonov 正則化を使用した Complex Partial-Systolic Matrix Solve Using Q-less QR Decomposition の実装
この例では、Complex Partial-Systolic Matrix Solve Using QR Decomposition ブロックを使用して、次に示す正則化された最小二乗行列方程式を解く方法を説明します。
![$$\left[\begin{array}{c}\lambda I_n\\A\end{array}\right]^\mathrm{H} \left[\begin{array}{c}\lambda I_n\\A\end{array}\right]X = (\lambda^2I_n + A^\mathrm{H}A)X = B$$](../../examples/fixedpoint/win64/ComplexPartialSystolicRegularizedQlessQRMatrixSolveExample_eq14445808551306013819.png)
ここで、A は m 行 n 列の行列 (m 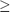 n)、B は n 行 p 列、X は n 行 p 列、
n)、B は n 行 p 列、X は n 行 p 列、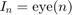 、
、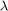 は正則化パラメーターです。
は正則化パラメーターです。
システム パラメーターの定義
この例の行列属性とシステム パラメーターを定義します。
m は、行列 A の行数です。ビームフォーミングや方向探知などの問題では、m は積分するサンプル数に対応します。
m = 100;
n は、行列 A の列数と行列 B および X の行数です。最小二乗問題では、m は n より大きく、通常、m は n より大幅に大きくなります。ビームフォーミングや方向探知などの問題では、n はセンサー数に対応します。
n = 10;
p は、行列 B および X の列数です。p 個の右辺をもつ系の同時求解に対応します。
p = 1;
この例では、行列 A のランクを列数未満に設定します。ビームフォーミングや方向探知などの問題では、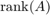 はセンサー アレイに作用する信号の数に対応します。
はセンサー アレイに作用する信号の数に対応します。
rankA = 3;
precisionBits は、行列解に必要な精度のビット数を定義します。この値はシステム要件に従って設定します。
precisionBits = 32;
正則化パラメーターを小さい正の値にすると、問題の調整を向上させ、推定値の分散を小さくすることができます。バイアスがありますが、推定値の分散が小さいと、多くの場合、最小二乗推定値と比べて平均二乗誤差が小さくなります。
regularizationParameter = 0.01;
この例では、複素数値の行列 A および B は、それらの要素の実数部と虚数部の大きさが 1 以下となるように構成されているため、任意の要素が取りうる最大絶対値は 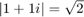 です。これらの値は各自のシステム要件によって定義されます。これらの内容が不明な場合に、
です。これらの値は各自のシステム要件によって定義されます。これらの内容が不明な場合に、A と B がシステムへの固定小数点入力である場合は、関数upperboundを使用して A と B の固定小数点型の上限を判別できます。
max_abs_A は、A の最大の大きさ要素に対する上限です。
max_abs_A = sqrt(2);
max_abs_B は、B の最大の大きさ要素に対する上限です。
max_abs_B = sqrt(2);
熱ノイズの標準偏差は、システム パラメーターである熱ノイズ パワーの平方根です。適切に設計されたシステムの量子化レベルは熱ノイズより低くなります。ここでは、thermalNoiseStandardDeviation を -50 dB のノイズ パワーと等価に設定します。
thermalNoiseStandardDeviation = sqrt(10^(-50/10))
thermalNoiseStandardDeviation =
0.0032
量子化ノイズの標準偏差は、必要な精度のビット数の関数です。これを計算するには、fixed.complexQuantizationNoiseStandardDeviationを使用します。これが thermalNoiseStandardDeviation 未満であることを確認します。
quantizationNoiseStandardDeviation = fixed.complexQuantizationNoiseStandardDeviation(precisionBits)
quantizationNoiseStandardDeviation = 9.5053e-11
固定小数点型の計算
この例では、設計されたシステム行列 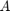 がフル ランクでなく (対象の信号の数が行列
がフル ランクでなく (対象の信号の数が行列 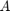 の列数より少ない)、測定されたシステム行列
の列数より少ない)、測定されたシステム行列 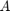 の加法性熱ノイズが量子化ノイズより大きいと仮定します。この加法性ノイズにより、測定された行列
の加法性熱ノイズが量子化ノイズより大きいと仮定します。この加法性ノイズにより、測定された行列 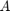 はフル ランクになります。
はフル ランクになります。
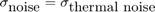 を設定します。
を設定します。
noiseStandardDeviation = thermalNoiseStandardDeviation;
関数fixed.complexQlessQRMatrixSolveFixedpointTypesを使用して固定小数点型を計算します。
T = fixed.complexQlessQRMatrixSolveFixedpointTypes(m,n,max_abs_A,max_abs_B,...
precisionBits,noiseStandardDeviation,[],regularizationParameter)
T =
struct with fields:
A: [0×0 embedded.fi]
B: [0×0 embedded.fi]
X: [0×0 embedded.fi]
T.A は、![$\left[\begin{array}{c}\lambda I_n\\A\end{array}\right]$](../../examples/fixedpoint/win64/ComplexPartialSystolicRegularizedQlessQRMatrixSolveExample_eq11993394244965770304.png) をオーバーフローしないようにインプレースで
をオーバーフローしないようにインプレースで ![$R=Q^\mathrm{H}\left[\begin{array}{c}\lambda I_n\\A\end{array}\right]$](../../examples/fixedpoint/win64/ComplexPartialSystolicRegularizedQlessQRMatrixSolveExample_eq00596422220803461583.png) に変換するために計算された型です。
に変換するために計算された型です。
T.A
ans =
[]
DataTypeMode: Fixed-point: binary point scaling
Signedness: Signed
WordLength: 39
FractionLength: 32
T.B は、B がオーバーフローしないようにするために計算された型です。
T.B
ans =
[]
DataTypeMode: Fixed-point: binary point scaling
Signedness: Signed
WordLength: 35
FractionLength: 32
T.X は、オーバーフローする可能性が低くなるような解 ![$X = \left(\left[\begin{array}{c}\lambda I_n\\A\end{array}\right]^\mathrm{H} \left[\begin{array}{c}\lambda I_n\\A\end{array}\right]\right) \backslash B$](../../examples/fixedpoint/win64/ComplexPartialSystolicRegularizedQlessQRMatrixSolveExample_eq13939041043834996947.png) を求めるために計算された型です。
を求めるために計算された型です。
T.X
ans =
[]
DataTypeMode: Fixed-point: binary point scaling
Signedness: Signed
WordLength: 50
FractionLength: 32
指定した型を使用して行列方程式を解く
rankA=rank(A) となるような乱数行列 A および B を作成します。ランダム測定ノイズを A に追加してこれをフル ランクにします。
rng('default');
[A,B] = fixed.example.complexRandomQlessQRMatrices(m,n,p,rankA);
A = A + fixed.example.complexNormalRandomArray(0,noiseStandardDeviation,m,n);
入力をfixed.complexQlessQRMatrixSolveFixedpointTypesで判別された型にキャストします。固定小数点に量子化することは、ランダム ノイズを追加することと等価です。
A = cast(A,'like',T.A); B = cast(B,'like',T.B); OutputType = fixed.extractNumericType(T.X);
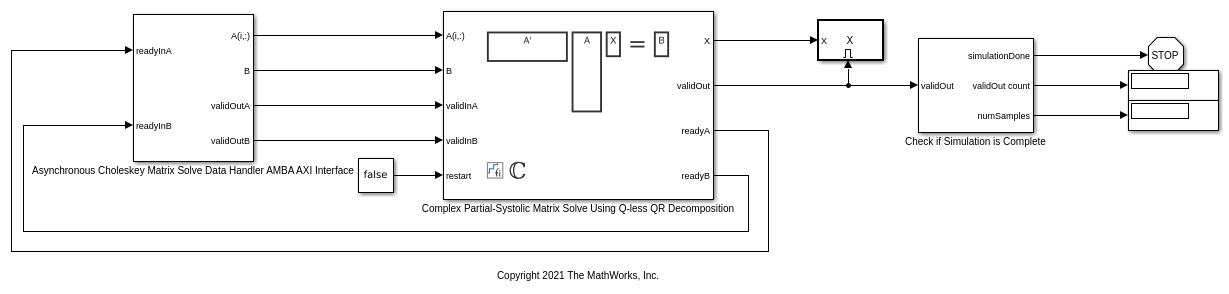
モデルを開く
model = 'ComplexPartialSystolicQlessQRMatrixSolveModel';
open_system(model);
モデル ワークスペースの変数の設定
補助関数 setModelWorkspace を使用して、上記で定義された変数をモデル ワークスペースに追加します。これらの変数は、Complex Burst Matrix Solve Using QR Decomposition ブロックのブロック パラメーターに対応します。
numOutputs = 1; % Number of recorded outputs aDelay = 1; % Delay of clock cycles between feeding in rows of A bDelay = 1; % Delay of clock cycles between feeding in B matrices fixed.example.setModelWorkspace(model,'A',A,'B',B,'m',m,'n',n,'p',p,... 'regularizationParameter',regularizationParameter,... 'aDelay',aDelay,'bDelay',bDelay,... 'numOutputs',numOutputs,'OutputType',OutputType);
モデルのシミュレーション
out = sim(model);
出力データからの解の構成
Complex Partial-Systolic Matrix Solve Using Q-less QR Decomposition ブロックは、各タイム ステップで行列 X を出力します。有効な結果の行列が出力されると、ブロックは validOut を true に設定します。
X = out.X;
出力の精度の検証
倍精度浮動小数点において、固定小数点出力と組み込み MATLAB® 関数間の相対誤差が小さいことを確認します。
![$$X_\textrm{double} = \left(\left[\begin{array}{c}\lambda I_n\\A\end{array}\right]^\mathrm{H} \left[\begin{array}{c}\lambda I_n\\A\end{array}\right]\right)\backslash B$$](../../examples/fixedpoint/win64/ComplexPartialSystolicRegularizedQlessQRMatrixSolveExample_eq02448525609591096686.png)
A_lambda = double([regularizationParameter*eye(n);A]); X_double = (A_lambda'*A_lambda)\double(B); relativeError = norm(X_double - double(X))/norm(X_double)
relativeError = 5.4974e-06
このファイルでは mlint の警告は非表示にします。
%#ok<*NASGU> %#ok<*ASGLU> %#ok<*NOPTS>
参考
Complex Partial-Systolic Matrix Solve Using Q-less QR Decomposition