HDL 用に最適化した正規化逆数の使用方法
この例では、関数 normalizedReciprocal および Normalized Reciprocal HDL Optimized ブロックを使用して入力の正規化逆数を計算する方法と、使用のタイミングを示します。
値の逆数は範囲が広くなることがあり、固定小数点型は浮動小数点型に比べて範囲が制限されます。入力値 u が小さければ 1/u は大きくなり、u が大きければ 1/u は小さくなります。したがって、1/u の固定小数点型には高い精度と広い範囲が求められ、長い語長が必要となります。
逆数と別の変数の積の範囲がわかっているアプリケーションでは、正規化逆数を計算し、それに他の変数を乗算してから、最終的な出力にシフトを適用すると効率的です。これには、たとえば、後退代入でピボット要素による除算が必要な最小二乗のアプリケーションなどが該当します。
正規化逆数の計算
入力を u とすると、正規化逆数 y および指数 e は、次のように計算されます。
(2.^e).*y = 1./u,
および
0.5 < |y| <= 1.
u = 0 で u が固定小数点またはスケーリングされた double の場合、y = 1 - eps(y) になります。
u = 0 で u が浮動小数点型の場合、y = inf になります。
u~=0 の場合、この関数が返すのは以下と等価になります。
[y,e] = log2(1./abs(double(u)))
y(u<0) = -y(u<0)異なる点はシフトと加算のみを使用して計算されることです。
MATLAB 関数または Simulink ブロックの選択
C コードの生成およびシステムの設計には、MATLAB® 関数 normalizedReciprocal を使用します。この関数ではレイテンシでの計算は行われません。シミュレーションでは、fiaccel、buildInstrumentedMex、または codegen を使用する速度について、関数を MEX ファイルにコンパイルします。
最適化された HDL コードを生成するには、Normalized Reciprocal HDL Optimized ブロックを使用します。このブロックは HDL において高いスループットを小さい面積で実現できるように最適化されており、生成された HDL コードと同じレイテンシでシミュレーションを行います。
結果の数値出力はブロックと関数で同じです。
MATLAB を使用した正規化逆数の計算
固定小数点入力 u の正規化逆数を計算し、その値を実際の逆数の値と比較します。
u = fi([-pi,0.01,pi])
u =
-3.1416 0.0100 3.1416
DataTypeMode: Fixed-point: binary point scaling
Signedness: Signed
WordLength: 16
FractionLength: 13
[y,e] = normalizedReciprocal(u)
y =
-0.6367 0.7806 0.6367
DataTypeMode: Fixed-point: binary point scaling
Signedness: Signed
WordLength: 16
FractionLength: 14
e =
1×3 int32 row vector
-1 7 -1
computed_reciprocal = 2.^double(e).* double(y)
computed_reciprocal = -0.3183 99.9141 0.3183
actual_reciprocal = 1./double(u)
actual_reciprocal = -0.3183 99.9024 0.3183
正規化逆数と実際の逆数の値が近いことがわかります。
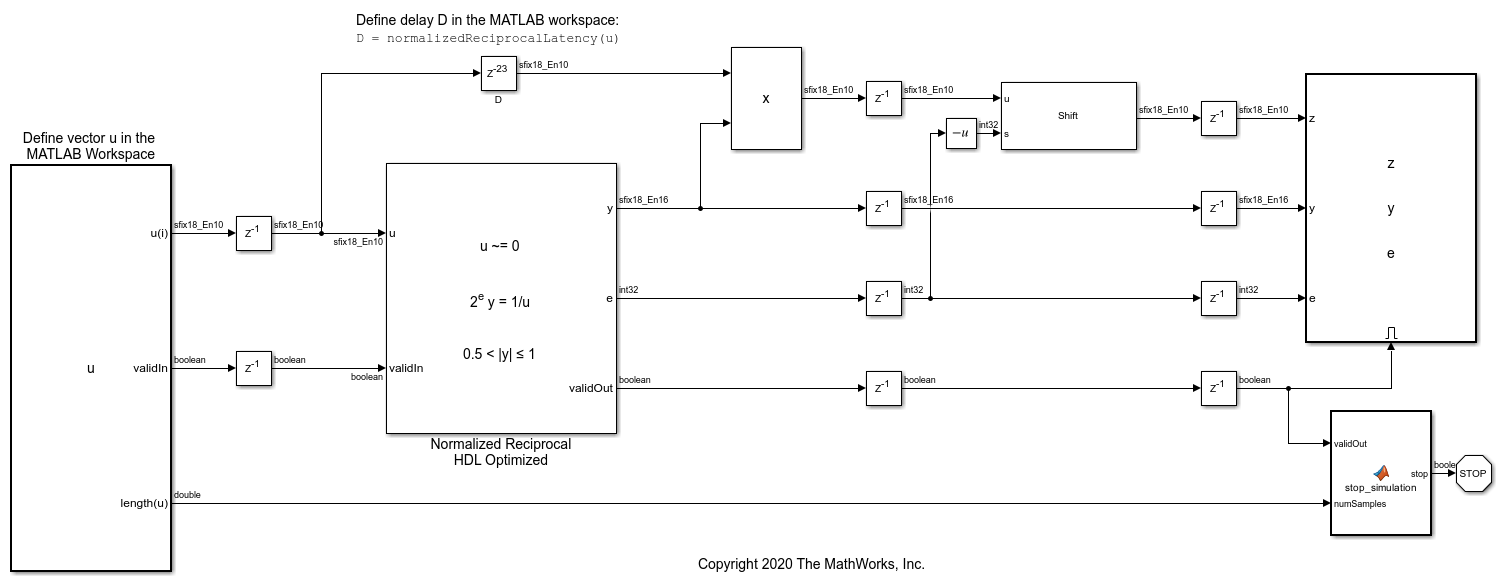
Simulink モデルの入力の定義
Normalized Reciprocal HDL Optimized ブロックを使用して、正規化逆数を取得する固定小数点入力 u を定義します。
x = linspace(0.001,100,100); x = [fliplr(-x),x]; u = fi(x,1,18);
Normalized Reciprocal HDL Optimized ブロックのレイテンシ
Normalized Reciprocal HDL Optimized ブロックは、二分探索を使用する入力を正規化することで機能します。二分探索のレイテンシは入力の語長の約 log2、それに続く CORDIC 逆数カーネルのレイテンシは入力の語長とほぼ同じです。
Normalized Reciprocal HDL Optimized ブロックは、常にデータを受け入れる準備ができています。最初のレイテンシの後、サンプルごとに有効なサンプルが出力されます。既定のパイプライン構成での符号付き固定小数点入力 u のサンプルのレイテンシは次のとおりです。
D = nextpow2(u.WordLength) + u.WordLength
この例に含まれている関数 normalizedReciprocalLatency を使用して、固定小数点、double、または single の数値型の入力のレイテンシを計算できます。
入力サンプルを Normalized Reciprocal HDL Optimized ブロックの出力と合わせるには、レイテンシ D を遅延で使用します。
D = normalizedReciprocalLatency(u,1)
D =
23
正規化逆数 Simulink モデルの実行
逆数と別の変数の積の範囲がわかっている簡単な例として、値の正規化逆数を計算し、それにその値自体を乗算します。この最終的な積は 1 と等しくなるはずです。入力値と逆数の範囲が広い場合でも、値とその逆数の積は既知の範囲になります。
0.5 < abs(y) <= 1 であり、積の大きさがこれよりも大きくなることはないため、積 u*y は u と同じ型で計算できることに注意してください。
model = 'NormalizedReciprocalModel';
open_system(model)
out = sim(model);
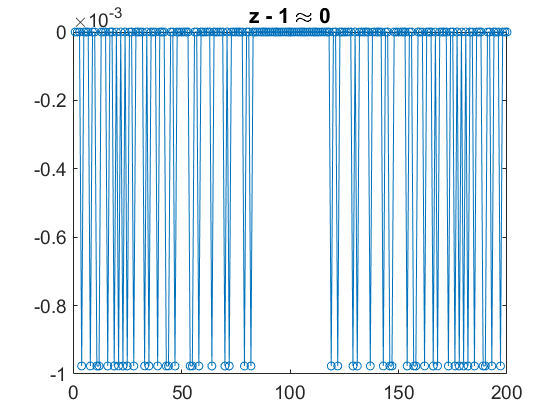
正規化逆数 Simulink モデルの結果の解析
次のプロットから、入力 u と逆数 1/u の範囲が広いのに対し、正規化逆数 y の範囲は -1 ~ 1 であることがわかります。
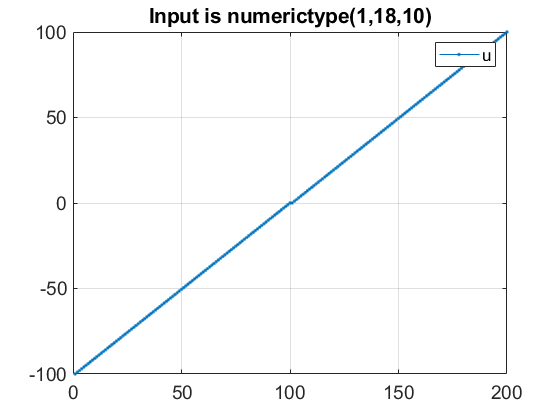
入力 u は -100 ~ 100 の範囲の fi 値のベクトルです。
normalizedReciprocalPlot(1,u,out.y,out.e,out.z);
逆数 1/u の実際の値は正規化逆数 (2.^e).*y とほぼ同じです。逆数 1/u は範囲が広いため、直線的な逆数を固定小数点で計算するにはハイ ダイナミック レンジのデータ型 (つまり語長と小数部が長いデータ型) が必要になります。
normalizedReciprocalPlot(2,u,out.y,out.e,out.z);

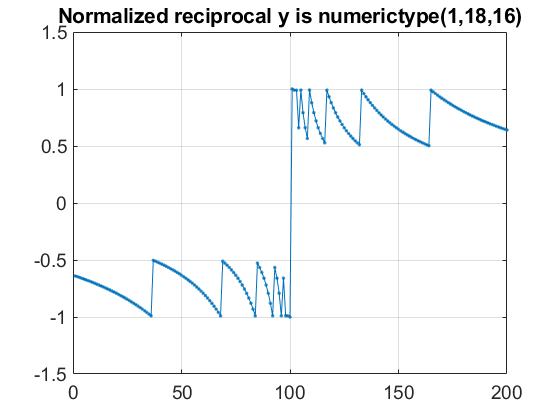
正規化逆数 y の範囲は次のとおりです。
0.5 < |y| <= 1
u と同じ語長のデータ型に効率的かつ正確に格納できます。y の数値型の小数部の長さは u の語長よりも 2 短くなります。この追加の整数ビットにより、y の正または負の区別に加え、値 -1 および +1 を正確に表現できます。
normalizedReciprocalPlot(3,u,out.y,out.e,out.z);
正規化指数 e と入力 u の大きさは逆相関関係にあります。u の大きさが大きいと、e は大きい負の値になります。u がゼロに近いと、e は大きい正の値になります。この関係を次に示します。
(2.^e).*y = 1./u,
normalizedReciprocalPlot(4,u,out.y,out.e,out.z);
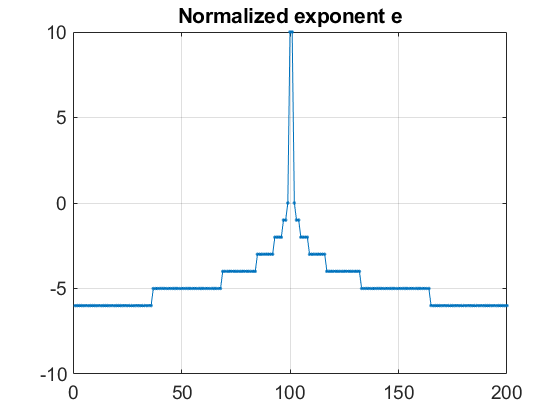
このモデルでは、正規化逆数 y に入力 u を乗算し、e でシフトして結果をスケーリングしています。y の大きさは 1 より小さいため、u の固定小数点型で積を計算できます。出力 z = 2^e (y * u) は 1 とほぼ等しくなります。
normalizedReciprocalPlot(5,u,out.y,out.e,out.z);
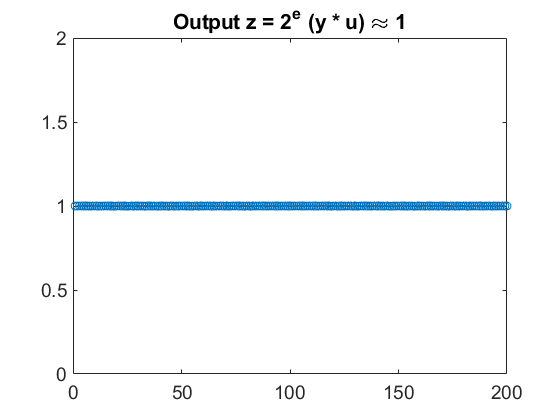
正規化逆数を固定小数点データ型で計算した結果として、出力 z には僅かな丸め誤差があります。
normalizedReciprocalPlot(6,u,out.y,out.e,out.z);