Specify GARCH Models

Default GARCH Model

The default GARCH(P,Q) model in Econometrics Toolbox™ is of the form

$${\epsilon }_t={\sigma }_t{z}_t,$$

with Gaussian innovation distribution and

$${\sigma }_t^2=\kappa +{\gamma }_1{\sigma }_{t-1}^2+\dots +{\gamma }_P{\sigma }_{t-P}^2+{\alpha }_1{\epsilon }_{t-1}^2+\dots +{\alpha }_Q{\epsilon }_{t-Q}^2.$$

The default model has no mean offset, and the lagged variances and squared innovations are at consecutive lags.

You can specify a model of this form using the shorthand syntax garch(P,Q). For the input arguments P and Q, enter the number of lagged conditional variances (GARCH terms), P, and lagged squared innovations (ARCH terms), Q, respectively. The following restrictions apply:

• P and Q must be nonnegative integers.

• If P is zero, the GARCH(P,Q) model reduces to an ARCH(Q) model.

• If P > 0, then you must also specify Q > 0.

When you use this shorthand syntax, garch creates a garch model with these default property values.

Property	Default Value
P	Number of GARCH terms, P
Q	Number of ARCH terms, Q
Offset	0
Constant	NaN
GARCH	Cell vector of NaNs
ARCH	Cell vector of NaNs
Distribution	"Gaussian"

To assign nondefault values to any properties, you can modify the created model using dot notation.

To illustrate, consider specifying the GARCH(1,1) model

$${\epsilon }_t={\sigma }_t{z}_t,$$

with Gaussian innovation distribution and

$${\sigma }_t^2=\kappa +{\gamma }_1{\sigma }_{t-1}^2+{\alpha }_1{\epsilon }_{t-1}^2.$$

Mdl = garch(1,1)

Mdl = 
  garch with properties:

     Description: "GARCH(1,1) Conditional Variance Model (Gaussian Distribution)"
      SeriesName: "Y"
    Distribution: Name = "Gaussian"
               P: 1
               Q: 1
        Constant: NaN
           GARCH: {NaN} at lag [1]
            ARCH: {NaN} at lag [1]
          Offset: 0

The created model, Mdl, has NaNs for all model parameters. A NaN value signals that a parameter needs to be estimated or otherwise specified by the user. All parameters must be specified to forecast or simulate the model.

To estimate parameters, input the model (along with data) to estimate. This returns a new fitted garch model. The fitted model has parameter estimates for each input NaN value.

Calling garch without any input arguments returns a GARCH(0,0) model specification with default property values:

DefaultMdl = garch

DefaultMdl = 
  garch with properties:

     Description: "GARCH(0,0) Conditional Variance Model (Gaussian Distribution)"
      SeriesName: "Y"
    Distribution: Name = "Gaussian"
               P: 0
               Q: 0
        Constant: NaN
           GARCH: {}
            ARCH: {}
          Offset: 0

Specify Default GARCH Model

This example shows how to use the shorthand garch(P,Q) syntax to specify the default GARCH(P, Q) model, $${\epsilon }_t={\sigma }_t{z}_t$$ with Gaussian innovation distribution and

$${\sigma }_t^2=\kappa +{\gamma }_1{\sigma }_{t-1}^2+\dots +{\gamma }_P{\sigma }_{t-P}^2+{\alpha }_1{\epsilon }_{t-1}^2+\dots +{\alpha }_Q{\epsilon }_{t-Q}^2.$$

By default, all parameters in the created model have unknown values.

Specify the default GARCH(1,1) model.

Mdl = garch(1,1)

Mdl = 
  garch with properties:

     Description: "GARCH(1,1) Conditional Variance Model (Gaussian Distribution)"
      SeriesName: "Y"
    Distribution: Name = "Gaussian"
               P: 1
               Q: 1
        Constant: NaN
           GARCH: {NaN} at lag [1]
            ARCH: {NaN} at lag [1]
          Offset: 0

The output shows that the created model, Mdl, has NaN values for all model parameters: the constant term, the GARCH coefficient, and the ARCH coefficient. You can modify the created model using dot notation, or input it (along with data) to estimate.

Using Name-Value Arguments

The most flexible way to specify GARCH models is using name-value arguments. You do not need, nor are you able, to specify a value for every model property. garch assigns default values to any properties you do not (or cannot) specify.

The general GARCH(P,Q) model is of the form

$$y_t=\mu +{\epsilon }_t,$$

where $${\epsilon }_t={\sigma }_t{z}_t$$ and

$${\sigma }_t^2=\kappa +{\gamma }_1{\sigma }_{t-1}^2+\dots +{\gamma }_P{\sigma }_{t-P}^2+{\alpha }_1{\epsilon }_{t-1}^2+\dots +{\alpha }_Q{\epsilon }_{t-Q}^2.$$

The innovation distribution can be Gaussian or Student’s t. The default distribution is Gaussian.

In order to estimate, forecast, or simulate a model, you must specify the parametric form of the model (for example, which lags correspond to nonzero coefficients, the innovation distribution) and any known parameter values. You can set any unknown parameters equal to NaN, and then input the model to estimate (along with data) to get estimated parameter values.

garch (and estimate) returns a model corresponding to the model specification. You can modify models to change or update the specification. Input models (with no NaN values) to forecast or simulate for forecasting and simulation, respectively. Here are some example specifications using name-value arguments.

Model	Specification
$$y_t={\epsilon }_t$$ $${\epsilon }_t={\sigma }_t{z}_t$$ zt Gaussian $${\sigma }_t^2=\kappa +{\gamma }_1{\sigma }_{t-1}^2+{\alpha }_1{\epsilon }_{t-1}^2$$	garch('GARCH',NaN,'ARCH',NaN) or garch(1,1)
$$y_t=\mu +{\epsilon }_t$$ $${\epsilon }_t={\sigma }_t{z}_t$$ zt Student’s t with unknown degrees of freedom $${\sigma }_t^2=\kappa +{\gamma }_1{\sigma }_{t-1}^2+{\alpha }_1{\epsilon }_{t-1}^2$$	garch('Offset',NaN,'GARCH',NaN,'ARCH',NaN,... 'Distribution','t')
$$y_t={\epsilon }_t$$ $${\epsilon }_t={\sigma }_t{z}_t$$ zt Student’s t with eight degrees of freedom $${\sigma }_t^2=0.1+0.6{\sigma }_{t-1}^2+0.3{\epsilon }_{t-1}^2$$	garch('Constant',0.1,'GARCH',0.6,'ARCH',0.3,... 'Distribution',struct('Name','t','DoF',8))

Here is a full description of the name-value arguments you can use to specify GARCH models.

Note

You cannot assign values to the properties P and Q. garch sets these properties equal to the largest GARCH and ARCH lags, respectively.

Name-Value Arguments for GARCH Models

Name	Corresponding GARCH Model Term(s)	When to Specify
Offset	Mean offset, μ	To include a nonzero mean offset. For example, 'Offset',0.3. If you plan to estimate the offset term, specify 'Offset',NaN. By default, Offset has value 0 (meaning, no offset).
Constant	Constant in the conditional variance model, κ	To set equality constraints for κ. For example, if a model has known constant 0.1, specify 'Constant',0.1. By default, Constant has value NaN.
GARCH	GARCH coefficients, $${\gamma }_1,\dots ,{\gamma }_P$$	To set equality constraints for the GARCH coefficients. For example, to specify the GARCH coefficient in the model $${\epsilon }_t=0.7{\sigma }_{t-1}^2+0.25{\epsilon }_{t-1}^2,$$ specify 'GARCH',0.7. You only need to specify the nonzero elements of GARCH. If the nonzero coefficients are at nonconsecutive lags, specify the corresponding lags using GARCHLags. Any coefficients you specify must satisfy all stationarity and positivity constraints.
GARCHLags	Lags corresponding to nonzero GARCH coefficients	GARCHLags is not a model property. Use this argument as a shortcut for specifying GARCH when the nonzero GARCH coefficients correspond to nonconsecutive lags. For example, to specify nonzero GARCH coefficients at lags 1 and 3, e.g., $${\sigma }_t^2={\gamma }_1{\sigma }_{t-1}^2+{\gamma }_3{\sigma }_{t-3}^2+{\alpha }_1{\epsilon }_{t-1}^2,$$ specify 'GARCHLags',[1,3]. Use GARCH and GARCHLags together to specify known nonzero GARCH coefficients at nonconsecutive lags. For example, if in the given GARCH(3,1) model $${\gamma }_1=0.3$$ and $${\gamma }_3=0.1,$$ specify 'GARCH',{0.3,0.1},'GARCHLags',[1,3].
ARCH	ARCH coefficients, $${\alpha }_1,\dots ,{\alpha }_Q$$	To set equality constraints for the ARCH coefficients. For example, to specify the ARCH coefficient in the model $${\epsilon }_t=0.7{\sigma }_{t-1}^2+0.25{\epsilon }_{t-1}^2,$$ specify 'ARCH',0.25. You only need to specify the nonzero elements of ARCH. If the nonzero coefficients are at nonconsecutive lags, specify the corresponding lags using ARCHLags. Any coefficients you specify must satisfy all stationarity and positivity constraints.
ARCHLags	Lags corresponding to nonzero ARCH coefficients	ARCHLags is not a model property. Use this argument as a shortcut for specifying ARCH when the nonzero ARCH coefficients correspond to nonconsecutive lags. For example, to specify nonzero ARCH coefficients at lags 1 and 3, e.g., $${\sigma }_t^2={\gamma }_1{\sigma }_{t-1}^2+{\alpha }_1{\epsilon }_{t-1}^2+{\alpha }_3{\epsilon }_{t-3}^2,$$ specify 'ARCHLags',[1,3]. Use ARCH and ARCHLags together to specify known nonzero ARCH coefficients at nonconsecutive lags. For example, if in the above model $${\alpha }_1=0.4$$ and $${\alpha }_3=0.2,$$ specify 'ARCH',{0.4,0.2},'ARCHLags',[1,3].
Distribution	Distribution of the innovation process	Use this argument to specify a Student’s t innovation distribution. By default, the innovation distribution is Gaussian. For example, to specify a t distribution with unknown degrees of freedom, specify 'Distribution','t'. To specify a t innovation distribution with known degrees of freedom, assign Distribution a data structure with fields Name and DoF. For example, for a t distribution with nine degrees of freedom, specify 'Distribution',struct('Name','t','DoF',9).

Specify GARCH Model Using Econometric Modeler App

You can specify the lag structure and innovation distribution of GARCH models using the Econometric Modeler app. The app treats all coefficients as unknown and estimable, including the degrees of freedom parameter for a t innovation distribution.

At the command line, open the Econometric Modeler app.

econometricModeler

Alternatively, open the app from the apps gallery (see Econometric Modeler).

In the app, you can see all supported models by selecting a time series variable for the response in the Time Series pane. Then, on the Econometric Modeler tab, in the Models section, click the arrow to display the models gallery.

The GARCH Models section contains all supported conditional variance models. To specify a GARCH model, click GARCH. The GARCH Model Parameters dialog box appear.

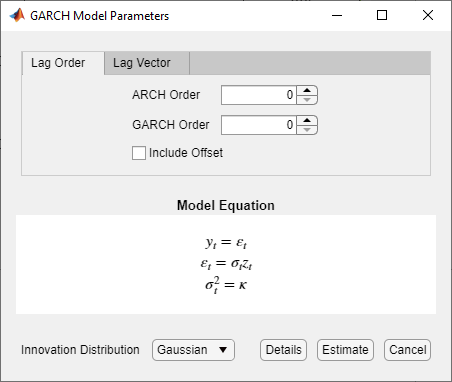
Adjustable parameters include:

• GARCH Degree – The order of the GARCH polynomial

• ARCH Degree – The order of the ARCH polynomial

• Include Offset – The inclusion of a model offset

• Innovation Distribution – The innovation distribution

As you adjust parameter values, the equation in the Model Equation section changes to match your specifications. Adjustable parameters correspond to input and name-value pair arguments described in the previous sections and in the garch reference page.

For more details on specifying models using the app, see Fitting Models to Data and Specifying Univariate Lag Operator Polynomials Interactively.

Specify GARCH Model with Mean Offset

This example shows how to specify a GARCH(P, Q) model with a mean offset. Use name-value pair arguments to specify a model that differs from the default model.

Specify a GARCH(1,1) model with a mean offset,

$$y_t=\mu +{\epsilon }_t,$$

where $${\epsilon }_t={\sigma }_t{z}_t$$ and

$${\sigma }_t^2=\kappa +{\gamma }_1{\sigma }_{t-1}^2+{\alpha }_1{\epsilon }_{t-1}^2.$$

Mdl = garch('Offset',NaN,'GARCHLags',1,'ARCHLags',1)

Mdl = 
  garch with properties:

     Description: "GARCH(1,1) Conditional Variance Model with Offset (Gaussian Distribution)"
      SeriesName: "Y"
    Distribution: Name = "Gaussian"
               P: 1
               Q: 1
        Constant: NaN
           GARCH: {NaN} at lag [1]
            ARCH: {NaN} at lag [1]
          Offset: NaN

The mean offset appears in the output as an additional parameter to be estimated or otherwise specified.

Specify GARCH Model with Known Parameter Values

This example shows how to specify a GARCH model with known parameter values. You can use such a fully specified model as an input to simulate or forecast.

Specify the GARCH(1,1) model

$${\sigma }_t^2=0.1+0.7{\sigma }_{t-1}^2+0.2{\epsilon }_{t-1}^2$$

with a Gaussian innovation distribution.

Mdl = garch('Constant',0.1,'GARCH',0.7,'ARCH',0.2)

Mdl = 
  garch with properties:

     Description: "GARCH(1,1) Conditional Variance Model (Gaussian Distribution)"
      SeriesName: "Y"
    Distribution: Name = "Gaussian"
               P: 1
               Q: 1
        Constant: 0.1
           GARCH: {0.7} at lag [1]
            ARCH: {0.2} at lag [1]
          Offset: 0

Because all parameter values are specified, the created model has no NaN values. The functions simulate and forecast don't accept input models with NaN values.

Specify GARCH Model with t Innovation Distribution

This example shows how to specify a GARCH model with a Student's t innovation distribution.

Specify a GARCH(1,1) model with a mean offset,

$$y_t=\mu +{\epsilon }_t,$$

where $${\epsilon }_t={\sigma }_t{z}_t$$ and

$${\sigma }_t^2=\kappa +{\gamma }_1{\sigma }_{t-1}^2+{\alpha }_1{\epsilon }_{t-1}^2.$$

Assume $$z_t$$ follows a Student's t innovation distribution with eight degrees of freedom.

tdist = struct('Name','t','DoF',8);
Mdl = garch('Offset',NaN,'GARCHLags',1,'ARCHLags',1,...
              'Distribution',tdist)

Mdl = 
  garch with properties:

     Description: "GARCH(1,1) Conditional Variance Model with Offset (t Distribution)"
      SeriesName: "Y"
    Distribution: Name = "t", DoF = 8
               P: 1
               Q: 1
        Constant: NaN
           GARCH: {NaN} at lag [1]
            ARCH: {NaN} at lag [1]
          Offset: NaN

The value of Distribution is a struct array with field Name equal to 't' and field DoF equal to 8. When you specify the degrees of freedom, they aren't estimated if you input the model to estimate.

Specify GARCH Model with Nonconsecutive Lags

This example shows how to specify a GARCH model with nonzero coefficients at nonconsecutive lags.

Specify a GARCH(3,1) model with nonzero GARCH coefficients at lags 1 and 3. Include a mean offset.

Mdl = garch('Offset',NaN,'GARCHLags',[1,3],'ARCHLags',1)

Mdl = 
  garch with properties:

     Description: "GARCH(3,1) Conditional Variance Model with Offset (Gaussian Distribution)"
      SeriesName: "Y"
    Distribution: Name = "Gaussian"
               P: 3
               Q: 1
        Constant: NaN
           GARCH: {NaN NaN} at lags [1 3]
            ARCH: {NaN} at lag [1]
          Offset: NaN

The unknown nonzero GARCH coefficients correspond to lagged variances at lags 1 and 3. The output shows only nonzero coefficients.

Display the value of GARCH.

Mdl.GARCH

ans=1×3 cell array
    {[NaN]}    {[0]}    {[NaN]}

The GARCH cell array returns three elements. The first and third elements have value NaN, indicating these coefficients are nonzero and need to be estimated or otherwise specified. By default, garch sets the interim coefficient at lag 2 equal to zero to maintain consistency with MATLAB® cell array indexing.